
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Сложные частотные фильтры 2 страница
|
|
|
|
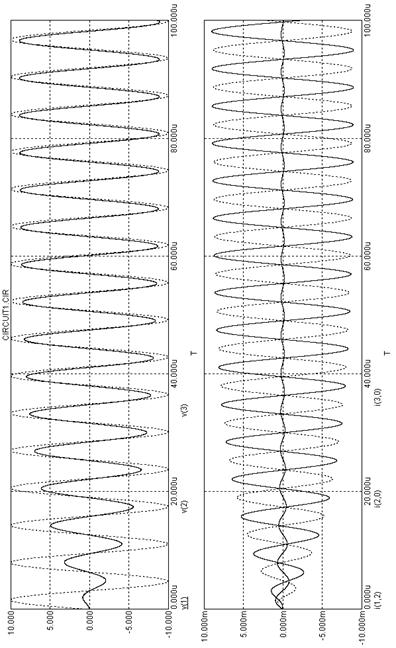
На рис. 5.15 приведены частотные характеристики цепи по передаче напряжения от узла 1 к узлу 2, по которым нетрудно определить напряжение на емкости (в узле 2).



5.10. Применение параллельного колебательного
контура
Параллельный колебательный контур чаще всего используется как элемент частотного фильтра аналогично последовательному контуру (пример будет рассмотрен далее), или как нагрузка активного элемента (транзистора) в резонансном усилителе сигнала. Пример схемы такого усилителя в моделирующем пакете MicroCAP7 показан на рис. 5.16.

Рис. 5.16
В состав усилителя входит импортный биполярный транзистор  типа 2N5190 (можно использовать отечественный аналог) с цепями питания по постоянному току
типа 2N5190 (можно использовать отечественный аналог) с цепями питания по постоянному току 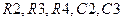 от источника
от источника  постоянного напряжения 15В, параллельный колебательный контур
постоянного напряжения 15В, параллельный колебательный контур 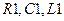 и источник гармонического входного сигнала с частотой
и источник гармонического входного сигнала с частотой 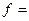 159,15 кГц.(
159,15 кГц.( рад/с), совпадающей с резонансной частотой контура, и амплитудой 4 мВ.
рад/с), совпадающей с резонансной частотой контура, и амплитудой 4 мВ.
На рис. 5.17 показаны временные диаграммы напряжений источника (верхняя кривая), выходного напряжения на коллекторе транзистора в узле 4 (нижняя кривая) и там же постоянное напряжение питания.


На рис. 5.18 представлены частотные характеристики резонансного усилителя (верхняя кривая – АЧХ, нижняя – ФЧХ). Коэффициент усиления равен примерно 3000 на частоте 151,6 кГц, что следует и из кривых на рис 5.17: амплитуда входного сигнала равна 3 мВ, а выходного 8,36 В (максимум АЧХ на рис. 5.18 несколько выше измеренного по временным диаграммам, так как она моделируется при весьма слабом сигнале).

Рис. 5.18
Проведите моделирование рассмотренной цепи самостоятельно, изменяя ее параметры. Введите неполное включение транзистора к контуру, сравните результаты.
5.11. Задания для самостоятельного решения
Задание 5.1. Вычислите резонансное сопротивление параллельного колебательного контура при 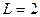 мГн,
мГн, 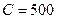 пФ,
пФ, 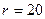 Ом.
Ом.
Задание 5.2. Определите резонансную частоту контура
при  кОм и С=1 нФ.
кОм и С=1 нФ.
Задание 5.3. Найдите напряжение на емкости параллельного контура в цепи рис. 5.19 при 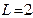 мГн,
мГн,  пФ,
пФ, 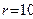 Ом,
Ом, 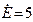 В,
В,  кОм,
кОм,  рад/с. Расчет проведите в координатах обобщенной расстройки.
рад/с. Расчет проведите в координатах обобщенной расстройки.

Рис. 5.19
Задание 5.5. Получите выражение для АЧХ цепи, показанной на рис. 5.20. Постройте график АЧХ при 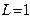 мГн,
мГн, 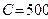 пФ,
пФ, 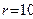 Ом,
Ом, 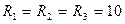 кОм. Проведите расчет в координатах обобщенной расстройки и абсолютной частоты, сравните результаты.
кОм. Проведите расчет в координатах обобщенной расстройки и абсолютной частоты, сравните результаты.
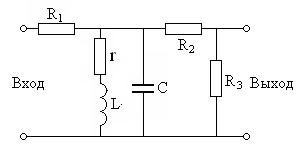
Рис. 5.20
6.1. Назначение частотных фильтров
В различных областях, связанных с электронной техникой (радиотехника, передача информации, биомедицинская электроника) возникает необходимость в частотной фильтрации сигналов на фоне помех. Например, в системах радиосвязи для работы каждой радиостанции выделяется определенная частотная область, как показано на рис. 6.1.

Рис. 6.1
Между несущими частотами  задан разнос
задан разнос 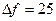 кГц, а каждая станция занимает полосу частот
кГц, а каждая станция занимает полосу частот  кГц. Для выделения полезного сигнала, например, на частоте
кГц. Для выделения полезного сигнала, например, на частоте  , и подавления всех других сигналов необходимо использовать частотный фильтр с полосовой АЧХ, как показано на рис. 6.1. Он должен пропускать сигнал в заданной полосе частот
, и подавления всех других сигналов необходимо использовать частотный фильтр с полосовой АЧХ, как показано на рис. 6.1. Он должен пропускать сигнал в заданной полосе частот  кГц и подавлять в заданное число раз (например, 1000) сигналы соседних станций, отстоящих от центральной частоты
кГц и подавлять в заданное число раз (например, 1000) сигналы соседних станций, отстоящих от центральной частоты  на величину
на величину
 кГц.
кГц.
Требуемое затухание соседних сигналов чаще задается в децибелах, в нашем примере 60 дБ.
6.2. Фильтры сосредоточенной селекции
Рассмотренные простые частотные фильтры не обеспечивают высокой избирательности. Фильтры сосредоточенной селекции (ФСС) обеспечивают высокую избирательность в заданной полосе частот за счет усложнения цепи.
Простейшими ФСС являются связанные колебательные контуры, пример схемы двухконтурного ФСС показан на рис.6.2. В теории цепей [2] для двух связанных контуров с одинаковыми элементами 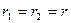 ,
,  и
и 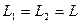 получено выражение для АЧХ вида
получено выражение для АЧХ вида
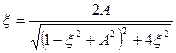 ,
,

где фактор связи  равен
равен
 ,
,
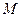 - взаимная ин-
- взаимная ин-
дуктивность связан- Рис. 6.2
ных (близко распо-
ложенных) катушек  и
и  ,
, 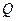 - добротность каждого контура.
- добротность каждого контура.
Графики нормированных АЧХ в виде отношения амплитуды тока во втором контуре к ее максимальному значению показаны на рис. 6.3. При малых  кривая подобна АЧХ одиночного колебательного контура, при
кривая подобна АЧХ одиночного колебательного контура, при 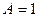 вершина кривой становится более плоской, а скаты круче, чем у одиночного контура, то есть избирательность становится выше. При
вершина кривой становится более плоской, а скаты круче, чем у одиночного контура, то есть избирательность становится выше. При 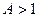 в полосе пропускания появляется провал (это допус-
в полосе пропускания появляется провал (это допус-
тимо, если глубина провала не велика) и скаты АЧХ становятся еще круче.
Таким образом, удается повысить избирательность фильтра за счет усложнения цепи.
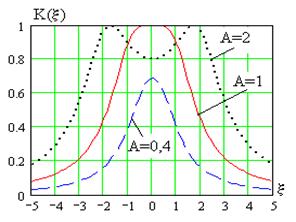
Рис. 6.3
6.3. Синтез частотных фильтров
Синтезом частотного фильтра называют формирование его схемы и определение параметров при заданной форме и параметрах требуемой АЧХ. Имеются методики синтеза фильтров с различными свойствами и необходимая справочная литература.
Значительно удобнее и, главное, быстрее синтезировать сравнительно простой фильтр с помощью специализированных или универсальных программ, например, MicroCAP7.
На рис. 6.4 показано задание на синтез частотного фильтра Баттерворта (равномерного в полосе пропускания) с центральной частотой 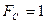 МГц, полосой пропускания
МГц, полосой пропускания  кГц и затуханием 60 дБ при отстройке на
кГц и затуханием 60 дБ при отстройке на 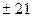 кГц от частоты
кГц от частоты  (
( кГц).
кГц).
При проектировании сложных частотных фильтров необходимо задать и поддерживать постоянными в полосе рабочих частот сопротивления источника сигнала и нагрузки, которые в рассматриваемом примере выбраны равными 50 Ом.
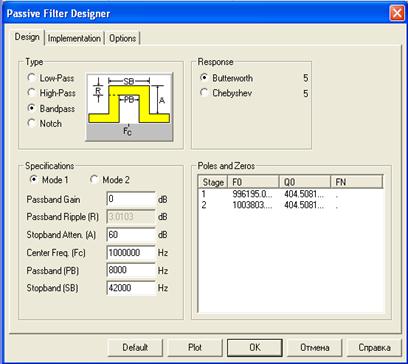
Рис. 6.4
Синтезированная программой MicroCAP7 схема фильтра показана на рис. 6.5. Он представляет собой соединение двух последовательных и трех параллельных колебательных контуров (последовательные контуры можно заменить эквивалентными емкостями) и обеспечивает АЧХ, показанную на рис. 6.6 (затемнены заданные границы, в которых должна находиться АЧХ).
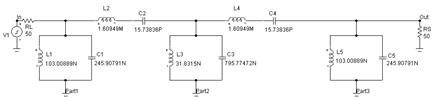
Рис. 6.5
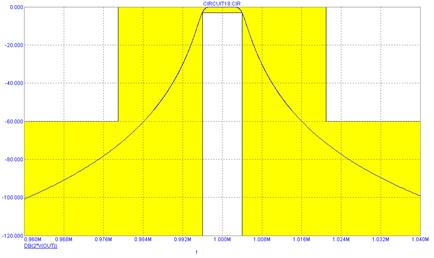
Рис. 6.6
Аналогично проведем синтез фильтра нижних частот чебышевского типа с полосой пропускания 200 Гц и высокой избирательностью: на уровне -20 дБ частота равна 218,6 Гц, а коэффициент прямоугольности –
 .
.
Синтезированная схема фильтра показана на рис. 6.7, а на рис. 6.8 – его АЧХ. Как видно, она имеет неравномерность в полосе пропускания, но более крутые скаты АЧХ при той же сложности, что и фильтр Баттерворта.

Рис. 6.7
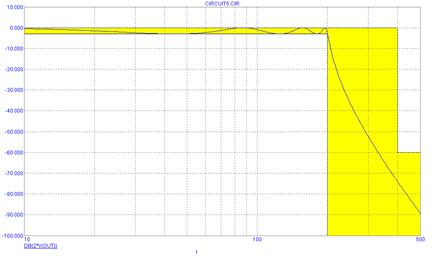
Рис. 6.8
Подобные ФНЧ можно использовать в биомедицинской технике при обработке сигналов.
 |
6.4. Пьезоэлектрические фильтры
Высококачественные частотные фильтры на базе реактивных элементов являются весьма сложными электрическими
цепями, трудоемкими и дорогими в изготовлении и настройке.
Высокоизбирательные узкополосные фильтры могут быть реализованы на базе кварцевого резонатора, условно показанного на рис. 6.9а. Это пластина, определенным образом вырезанная из монокристалла кварца, на противоположные грани которой нанесены металлические обкладки с подключенными к ним проволочными выводами.
В кварцевой пластине имеет место явление пьезоэффекта: при подаче на металлические электроды переменного напряжения определенной частоты в ней возникают механические колебания и, наоборот, при возникновении в пластине механических колебаний на ее гранях возникает переменное напряжение.
Эквивалентная электрическая схема кварцевого резонатора показана на рис. 6.9б. Ее особенностью является очень малые сопротивление потерь  (доли Ома) и емкость
(доли Ома) и емкость 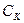 (доли пикофарады).
(доли пикофарады).

Рис. 6.9.
На частоте

имеет место резонанс напряжений в последовательном контуре 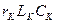 , а на частоте
, а на частоте
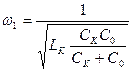
- резонанс токов в параллельном колебательном контуре  . На рис. 6.10 показаны зависимости от частоты модуля
. На рис. 6.10 показаны зависимости от частоты модуля  , активной
, активной 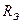 и реактивной
и реактивной  составляющих сопротивления цепи рис. 6.9б при
составляющих сопротивления цепи рис. 6.9б при 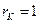 Ом,
Ом, 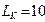 мГн,
мГн,  пФ и
пФ и  пФ. Обратите внимание, в каком узком диапазоне частот резко меняются сопротивления кварцевого резонатора.
пФ. Обратите внимание, в каком узком диапазоне частот резко меняются сопротивления кварцевого резонатора.

Рис. 6.10
Таким образом, на базе кварцевого резонатора в окрестности частоты 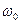 можно реализовать высокочастотные (например,
можно реализовать высокочастотные (например, 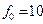 МГц) весьма узкополосные (
МГц) весьма узкополосные ( Гц) фильтры с высокой избирательностью. Это обусловлено высокой добротностью кварцевого резонатора (до нескольких миллионов, в примере на рис. 6.10 получим
Гц) фильтры с высокой избирательностью. Это обусловлено высокой добротностью кварцевого резонатора (до нескольких миллионов, в примере на рис. 6.10 получим 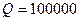 ) за счет малых потерь энергии механических колебаний в монокристалле кварца (горного хрусталя). Благодаря этой особенности из него изго-
) за счет малых потерь энергии механических колебаний в монокристалле кварца (горного хрусталя). Благодаря этой особенности из него изго-
тавливают хрустальные бокалы с очень продолжительным «звоном».
Высокодобротные колебательные системы (например, кварцевые резонаторы) крайне необходимы для реализации генераторов гармонических колебаний с высокой стабильностью частоты, например в электронных часах.
В радиотехнике широкое применение получили пьезоэлектрические частотные фильтры на поверхностных акустических волнах (ПАВ). Они обеспечивают АЧХ с высокой прямоугольностью (эквивалентный порядок электрической цепи на реактивных элементах 100-200) и широко применяются, например, в телевизионных приемниках.
6.5. Активные RC фильтры
Частотные пассивные (без усилителей сигнала) LC фильтры включают в себя катушки индуктивности, которые достаточно сложны в изготовлении, дороги и плохо поддаются миниатюризации. С этой точки зрения удобнее безындуктивные или RC фильтры. Однако в этом случае сложно реализовать фильтры с высокой избирательностью и в них часто будет наблюдаться значительное затухание сигнала в полосе пропускания.
Широкое применение на практике находят активные RC фильтры на базе операционных усилителей (ОУ), условное обозначение которого показано на рис. 6.11а. Усилитель имеет два входа: неинвертирующий  и инвертирующий
и инвертирующий  , один выход
, один выход 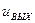 и выполняет операцию вида
и выполняет операцию вида
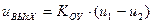 ,
,
где 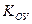 - коэффициент усиления ОУ, который зависит от частоты сигнала, как показано на рис. 6.11б (обе оси в логарифмическом масштабе).
- коэффициент усиления ОУ, который зависит от частоты сигнала, как показано на рис. 6.11б (обе оси в логарифмическом масштабе).
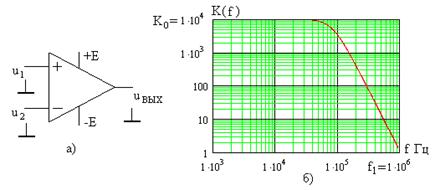 Рис. 6.11
Рис. 6.11
Максимум  имеет место на низких частотах и лежит в пределах от нескольких сотен до сотен тысяч (в примере
имеет место на низких частотах и лежит в пределах от нескольких сотен до сотен тысяч (в примере 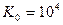 ). Затем он медленно падает до уровня
). Затем он медленно падает до уровня 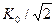 (на 3 дБ) в полосе пропускания, а далее снижается до 1 на частоте единичного усиления
(на 3 дБ) в полосе пропускания, а далее снижается до 1 на частоте единичного усиления  . Входное сопротивление ОУ весьма велико (например, 1 МОм) и его можно считать бесконечным, а выходное – мало (например, 0,1 Ом), практически равно нулю.
. Входное сопротивление ОУ весьма велико (например, 1 МОм) и его можно считать бесконечным, а выходное – мало (например, 0,1 Ом), практически равно нулю.

Пример схемы активного RC фильтра нижних частот второго порядка показан на рис. 6.12. Синтез активных RC фильтров с заданными частотными характеристиками можно проводить в пакете программ MicroCAP7, пример модели показан на рис. 6.13, а его АЧХ и ФЧХ показаны на рис. 6.14 (в верхней и нижней частях соответственно).
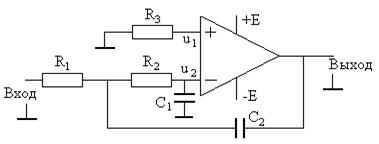
Рис.6.12

Рис. 6.13
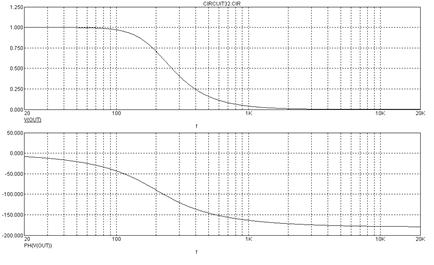
Рис. 6.14
Подобный фильтр может применяться, например, в биомедицинской аппаратуре для выделения сигналов.
6.6. Задания для самостоятельного решения
Задание 6.1. На рис. 6.15 в частотном диапазоне показаны области, занимаемые сигналами двух радиостанций - полезной на частоте  и мешающей на частоте
и мешающей на частоте  , а пунктирной линией - трапециидальная АЧХ фильтра, выделяющего полезный сигнал. Определите минимальный коэффициент прямоугольности
, а пунктирной линией - трапециидальная АЧХ фильтра, выделяющего полезный сигнал. Определите минимальный коэффициент прямоугольности  фильтра при
фильтра при 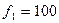 МГц,
МГц, 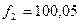 МГц и
МГц и 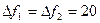 кГц.
кГц.

Рис. 6.15
Задание 6.2. В условиях задания 6.1 получите общую формулу для  , постройте график зависимости коэффициента прямоугольности от разноса частот
, постройте график зависимости коэффициента прямоугольности от разноса частот  . Вычислите при указанных выше данных разнос частот
. Вычислите при указанных выше данных разнос частот 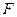 , при котором
, при котором  .
.
|
|
|
|
|
Дата добавления: 2014-11-25; Просмотров: 809; Нарушение авторских прав?; Мы поможем в написании вашей работы!