Общие положения теории функций комплексного переменного

РЕШЕНИЕ ПЛОСКИХ ЗАДАЧ ФИЛЬТРАЦИИ МЕТОДАМИ ТЕОРИИ ФУНКЦИЙ КОМПЛЕКСНОГО ПЕРЕМЕННОГО

ВОПРОСЫ ДЛЯ САМОПРОВЕРКИ

1. Основные виды задач по заданию режима работы скважин.

2. Сущность метода суперпозиции.

3. Потенциал сложного потока.

4. Уравнения эквипотенциальных поверхностей.

5. Метод отображения источников и стоков.

6. Фильтрационный поток от нагнетательной скважины к эксплуатационной (выражение для потенциала, изобара, поле течения).

7. Фильтрационный поток от нагнетательной скважины к эксплуатационной (выражение для массового дебита, модуль массовой скорости, время и площадь обводнения).

8. Приток к группе скважин с удаленным контуром питания.

9. Приток к скважине в пласте с прямолинейным контуром питания.

10. Приток к скважине, расположенной вблизи непроницаемой прямолинейной границы.

11. Приток к скважине в пласте с произвольным контуром питания.

12. Приток к скважинам кольцевой батареи (дебит скважины и батареи). Что такое – эксцентрично расположенная скважина?

13. Приток к скважинам кольцевой батареи (поле течения, оценки эффекта взаимодействия).

14. Приток к прямолинейной батарее скважин (конечное число скважин). В чем отличие формул Голосова для четного и нечетного числа скважин?

15. Приток к прямолинейной батарее скважин (бесконечное число скважин).

16. Метод Борисова (сущность, внутреннее и внешнее сопротивления).

17. Интерференция несовершенных скважин.

18. Взаимодействие скважин в анизотропном пласте (батарея расположена во внутренней неоднородности кругового пласта).

19. Взаимодействие скважин в неоднородно проницаемом и анизотропном пластах (батарея расположена во внешней неоднородности кругового пласта).

20. Периодически работающая скважина. Уравнение КВД.

21. Влияние радиуса скважины на дебит при взаимодействии скважин.

  Рис. 8.1. Ортогональность изобар и линий тока

Круг задач, рассмотренных в предыдущем разделе, может быть значительно расширен, если к решениям применить аппарат теории функций комплексного переменного. При этом оказывается возможным исследовать отдельные вопросы плоского потока более полно. Рассмотрим связь между задачами плоского фильтрационного потока и теорией функций комплексного переменного.

Совместим с основной плоскостью течения плоскость комплексного переменного z = х + iy. Каждое комплексное число z изображается в этой плоскости точкой М (х, у) (рис. 8.1.). Функцией комплексного переменного z будет комплексное переменное F (z), если указан закон, позволяющий получить значение F (z) no заданному значению z.

Отделив в функции F (z) действительную часть от мнимой, можем записать

F (z) = F (х + iy) = j (х, у) + iy (х, у),(8.1)

где j (х, у) и y (х, у) - некоторые функции действительных переменных х и у; i – мнимая единица.

Задать функцию комплексного переменного - значит задать соответствие между парами чисел (х, у) и (j, y). Функция F (z) является аналитической в точке z_m, то есть имеющей производную во всех точках некоторой окрестности z_m.

В теории функций комплексного переменного имеются следующие положения:

8. Каждые две кривые, из которых одна принадлежит семейству кривых, определяемых уравнением j (х, у) = С, а другая - семейству кривых y (х, у) = С^* (С и С^* – постоянные), пересекаются под прямым углом, т. е. два семейства кривых образуют ортогональную сетку в основной плоскости течения.

2. Функции j (х, у)и y (х, у)удовлетворяют уравнению Лапласа, то есть

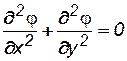; (8.2)

. (8.3)

Положения 1 и 2 справедливы, если выполняются такие условия:

. (8.4)

Условия (8.4) называются уравнениями Коши – Римана.

Дата добавления: 2014-11-25