Краткая теория

Изучение закона сохранения энергии на примере маятника Максвелла

Цель работы: изучить закон сохранения энергии

Оборудование:

1. Маятник Максвелла;

2. Линейка;

3. Секундомер;

4. Штангенциркуль.

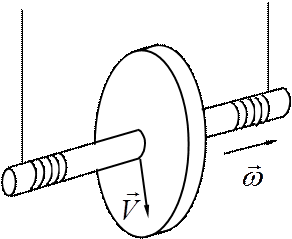
Маятник Максвелла представляет собой маховик с радиусом R на оси радиуса r (см. рис. 1).

	Рис. 1. Схема маятника Максвелла

На эту ось с двух сторон наматываются нити, в результате чего маховик поднимается на высоту h. При освобождении маховик движется вниз и раскручивается под действием момента, создаваемого силами натяжения нитей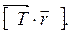

Линейное ускорение 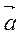, направленное вниз, маятник приобретает под действием разности сил натяжения нитей и силы тяжести. Найдем это ускорение, пренебрегая силами сопротивления. Из следствия из второго закона Ньютона: ma = mg – T; согласно основному уравнению динамики вращательного движения: 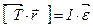(*). Учитывая, что момент инерции маховика: 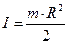(моментом инерции оси можно пренебречь, моментом инерции тела относительно оси называется сумма произведений масс всех материальных точек тела на квадраты их расстояний до оси), и выразив угловое ускорение через линейное: 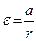, уравнение (*) можно представить в скалярном виде: 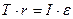, тогда решая полученную систему уравнений: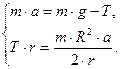

Можно получить: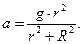

По закону сохранения и превращения энергии (в замкнутой системе энергия может переходить из одних видов в другие и предаваться от одного тела другому, но ее общее количество остается неизменнной), если маятник Максвелла спустится с высоты h, то часть его потенциальной энергии mgh перейдет в кинетическую энергию поступательного движения 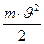и кинетическую энергию вращательного движения 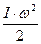, а часть пойдет на совершение работы А против сил сопротивления:

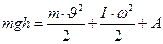
(1)

Выразив угловую скорость маховика через линейную получим из (1):

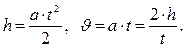
(2)

При равноускоренном движении без начальной скорости

Таким образом, измерив время спуска маятника Максвелла, можно найти его линейную скорость в нижней точке υ и, используя (2), определить работу сил сопротивления. Зная А, можно рассчитать момент сил сопротивления (моментом сил называется по формуле:

(3)

Дата добавления: 2014-11-25