Загальна постановка задачі

АНАЛІТИЧНІ МЕТОДИ розв’язування ЗДЛП

ГРАФІЧНИМ МЕТОДОМ

ДЕЯКІ ОСОБЛИВОСТІ Розв’язування ЗДЛП

Розв’язування задачі в середовищі Mathcad

I

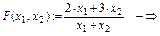
Given

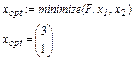
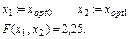
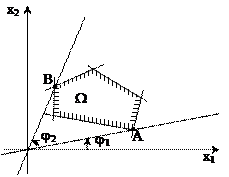
1. ОПР обмежена знизу й зверху

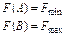
2. Багатогранник розв’язків необмежений, однак на ньому існують точки, у яких цільова функція досягає свого оптимуму

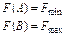
3. Багатогранник розв’язків необмежений, однак один з экстремумов існує

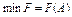
Задача має так званий асимптотичнтй максимум, тобто .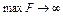

4. Багатогранник розв’язків необмежений, задача має асимптотичні оптимуми

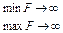
Необхідно знайти оптимум наступної функції:

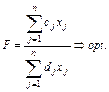(3.10)

Задача вирішується при обмеженнях виду:

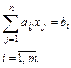(3.10)

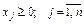. (3.11)

Задача (3.10)–(3.11) може бути зведена до задачі лінійного програмування. Для цього необхідно ввести нові змінні, при цьому 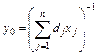. У такому випадку здійснюється перехід в область нових змінних, на підставі співвідношень виду:

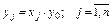. (3.12)

З використанням нових змінних, задача (3.10)-(3.11) зводиться до наступної ЗЛП:

(3.12)

при обмеженнях виду:

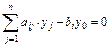(3.13)

і рівняннях зв'язків виду

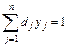(3.14)

Задача вирішується при умовах невід’ємності, що накладають на n змінних

;

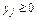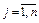. (3.15)

.

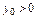Задача (3.12)-(3.15) є задачею лінійного програмування, отже, розв’язуючи її відомими методами можна знайти відповідні розв’язки. При цьому, одержавши оптимальний план такої задачі, на підставі співвідношень (3.12) можна знайти оптимальний план вихідної задачі (3.10)-(3.11). Таким чином, можна вказати наступний алгоритм розв’язування ЗДЛП.

I. Вихідну ЗДЛП (3.10)-(3.11) зводять до ЗЛП (3.12)-(3.15).

II. Знаходять оптимальний план ЗЛП відомими методами.

III. Використовуючи співвідношення (3.12) знаходять оптимальний план вихідної задачі.

IV. Підставляючи значення x_j, при 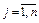у вираз для функції (3.10) отримують оптимальне значення цільової функції вихідної задачі.

Приклад. Знайти максимальне значення функції:

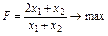; (3.16)

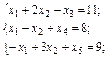(3.17)

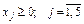. (3.18)

Зведемо дану задачу до ЗЛП, при цьому

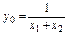. (3.19)

Далі вводимо нові змінні:

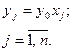(3.20)

Тоді вихідна задача (3.16)-(3.18) зводиться до наступної ЗЛП

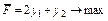. (3.19)

Задача вирішується в рамках обмежень виду:

(3.20)

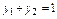; (3.21)

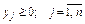; (3.22)

.

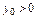Задача (3.19)-(3.22) є ЗЛП і розв’язок її можна знайти методом штучного базису. Для цього формулюють наступну розширену задачу

;

;

;

.

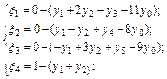
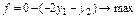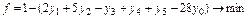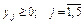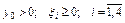Далі розширену задачу заносять у первісну симплексну таблицю

		з1	з2	з3	з4	з5	з0
x 1						–1			–11
x 2							–8
x 3		–1					–9	Þ
x 4
F		–2	–1
f				–1			–28

		з2	з3	з4	з5	з0
в 1			–1			–11
x 2		–3
x 3			–1			–20	Þ
x 4		–1
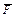
		+3	–2			–22
f						–6

		з2	з3	з4	з0
в 1			–1		–11
x 2		–3
в 5			–1		–20	Þ
x 4		–1
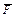
			–2		–22
f		–4

		з2	з3	з4
в 1		–27
в 0		–3
в 5		–45			:(3)	Þ
x 4			–8	–11
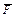
		–57
f			–8	–11

		з2	з3	з4
в 1		–9	8/3	11/3
в 0		–1	1/3	1/3
в 5		–15	17/3	20/3	Þ
x 4					–8/3	–11/3
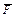
		–19	16/3	22/3
f			–8/3	–11/3

		з3	з4
в 1
в 0
в 5				Þ
в 2		–8/3	–11/3
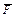
		8/3	11/3
f

Далі розділивши останню таблицю на 10, одержують оптимальний план ЗЛП

		з3	з4
в 1	9/10
в 0	1/10
в 5	15/10
в 2	1/10	–8/30	–11/30
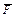
	19/10	8/30	11/30

Висновок: у процесі визначення первісного опорного плану робоча точка пошуку экстремума вийшла в ту вершину опуклого багатогранника, що є точкою максимуму.

.

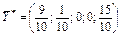
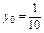З урахуванням того, що 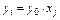, знаходять оптимальний план ЗДЛП

.

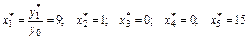
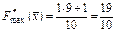розв’язування задачі в середовищі Mathcad:

Дата добавления: 2014-11-25