
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Связевые системы с однотипными
|
|
|
|
диафрагмами с проёмами
Диафрагмы могут иметь различное число проёмов: с одним рядом несимметрично расположенных проёмов (рис. 36) или с несколькими незначительно отличающихся по ширине проёмами (рис. 37).
Вертикальную диафрагму с проёмами рассматривают как многоэтажную раму, у которой стойки – простенки, а ригели – перемычки. Поскольку в такой раме жёсткость стоек-простенков во много раз больше жесткости ригелей-перемычек, при определении сдвиговой жесткости К считают, что 1/s - величина,
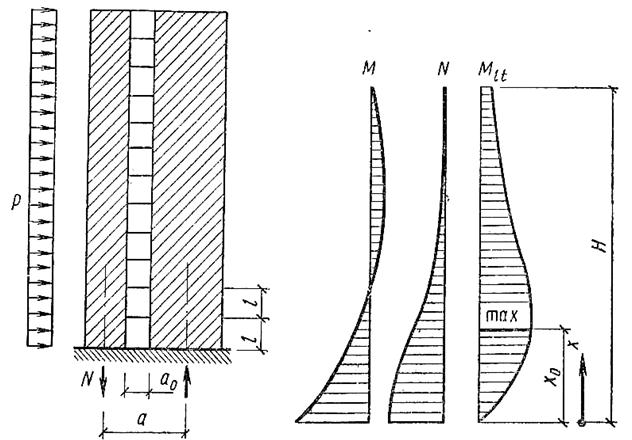
Рис. 36. К расчёту диафрагмы с одним рядом несимметрично расположенных проёмов
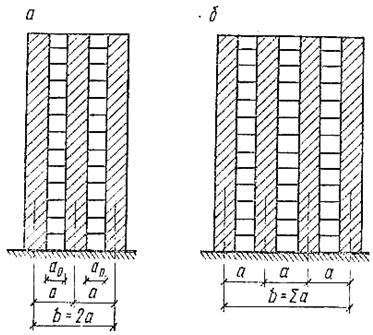
| Рис. 37. К расчёту диафрагмы а – с двумя рядами проёмов; б – с несколькими рядами проёмов |
что 1/s - величина, малая в сравнении с 1/r. Тогда, согласно формуле (13), сдвиговая жёсткость диафрагмы с проемами
К=12r/l, (53)
где  — суммарная погонная жесткость перемычек одного яруса диафрагмы с несколькими рядами проёмов.
— суммарная погонная жесткость перемычек одного яруса диафрагмы с несколькими рядами проёмов.
Кроме того, следует учесть, что ригели-перемычки только в пределах проёмов имеют конечную жесткость Вlt, но в пределах широких простенков становятся абсолютно жесткими. В таких случаях усредненная по всему пролету жёсткость перемычки составляет Blt·γ3, где γ=а/а0; а — расстояние между осями простенков; а0 — расстояние между простенками в свету. Погонная жёсткость перемычки
ilt = Blt·γ3 /aφ. (54)
Коэффициентом φ учитывают влияние деформаций сдвига перемычки. Полагая Gb=0,5Eb получают
φ= 1+2,4(hlt·/ а0), (55)
где hlt — высота сечения перемычки.
Суммарная изгибная ж`сткость простенков диафрагмы B=∑Bj, где Bj — изгибная жесткость отдельного простенка. Если диафрагмы в системе сплошные и с про`мами (см. рис. 27, б),то суммарная изгибная жёсткость Bdg+∑Bj.
Характеристика жесткости диафрагмы с проемами согласно (25), (23)


Заметим, что при λ≥3 в расчетных формулах усилий и перемещений можно принять chλ=shλ,; χ=λ.
Изгибную жесткость вертикальной диафрагмы В0 (по сечению с проёмами за вычетом жесткости простенков относительно своих осей) определяют по формуле (32). Для диафрагм в этой формуле расстояние между осями крайних простенков b=∑a., при одном ряде проемов b=a.
В общем уравнении (21) и его решении (24) краевые условия для вертикальных диафрагм с проёмами остаются такими же, как и для рамно-связевых систем. Поэтому для расчета диафрагм с проёмами следует применять уравнения перемещений и прогибов (41), уравнения изгибающих моментов и продольных сил простенков (42) и (45).
Выражение поперечных сил перемычек диафрагмы
 (56)
(56)
В симметричной диафрагме с двумя рядами проемов поперечные силы перемычек одного яруса равны. В диафрагме с несколькими рядами проемов это равенство принимают как допущение.
Изгибающий момент перемычек по грани проема (рис. 38)в предположении, что нулевая точка моментов расположена в середине пролета в свету
 (57)
(57)
Эпюры усилий вертикальной связевой диафрагмы с проемами приведены на рис. 36. На эпюре Мlt координату максимума определяют (как и для рамно-связевой системы) из уравнения (46). Изгибающие моменты отдельных простенков определяют из суммарного момента М пропорционально их жесткостям.

| 
|
| Рис. 38. Эпюра моментов перемычки диафрагмы с проёмом Рис. 39. Линия изгиба диафрагмы 1 – с проёмами при λ=1…9 и v2=1,1; 2 - сплошной |
Согласно уравнению равновесия обобщенных поперечных сил, поперечная сила от внешней нагрузки уравновешивается производной от изгибающего момента простенков и распределенным моментом перемычек  , т.е.
, т.е.
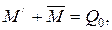 (58)
(58)
где  (59)
(59)
Поперечная сила отдельного простенка
 (60)
(60)
здесь a1, a2 — расстояния от оси простенка до нулевой точки моментов перемычки слева и справа.
Линия изгиба вертикальной диафрагмы с проемами близка по очертанию к линии изгиба консольной балки. На рис. 39изображена линия изгиба диафрагм с диапазоном значений характеристики жёсткости λ= 1…9 при v2 =1,1.
Прогиб верхнего яруса диафрагмы с проёмами согласно формуле (41) можно представит как сумму двух прогибов f = f1 + f0: вызванного податливостью перемычек f1 и вызванного общим изгибом диафрагмы f0
|
|
|
|
|
Дата добавления: 2014-11-25; Просмотров: 610; Нарушение авторских прав?; Мы поможем в написании вашей работы!