
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Часть 2. Статически неопределимые стержневые системы 2 страница
|
|
|
|
Так как модули упругости всех стержней одинаковы и площади 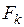 всех сечений выражаются через площадь
всех сечений выражаются через площадь 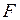 , то вместо (8.1) удобнее использовать выражения
, то вместо (8.1) удобнее использовать выражения
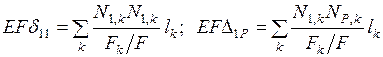 . (8.2)
. (8.2)
Учитывая симметрию, в расчет можно включать только половину фермы. При этом длины стержней, не имеющих парного стержня во второй половине, следует уменьшить вдвое. После подсчета величин 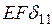 и
и 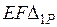 следует определить значение неизвестного:
следует определить значение неизвестного: 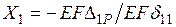 . Окончательные значения сил в стержнях фермы определяются по формуле
. Окончательные значения сил в стержнях фермы определяются по формуле 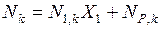 . Для осуществления кинематической проверки используется выражение
. Для осуществления кинематической проверки используется выражение
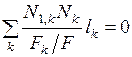 . (8.3)
. (8.3)
Все расчеты свести в таблицу.
 Пример выполнения задания
Пример выполнения задания
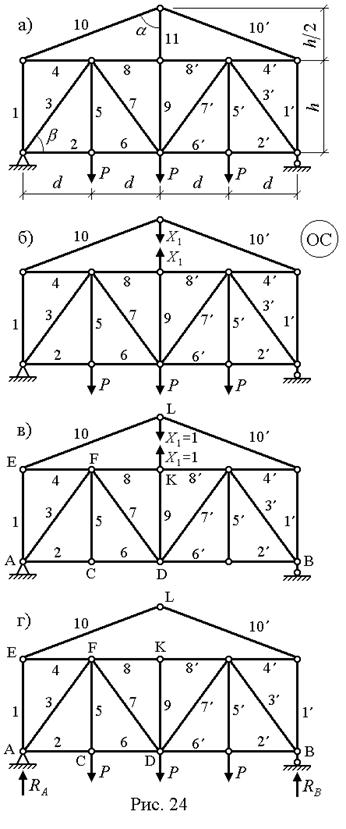
Дано: схема фермы (рис. 24а); 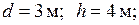
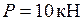 . Площади поперечных сечений стержней фермы: нижнего пояса -
. Площади поперечных сечений стержней фермы: нижнего пояса - 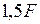 ; верхнего пояса -
; верхнего пояса - 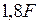 ; решетки -
; решетки - 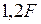 ; элементов шпренгеля -
; элементов шпренгеля -  . Требуется: а) определить силы во всех стержнях фермы; б) выполнить кинематическую проверку.
. Требуется: а) определить силы во всех стержнях фермы; б) выполнить кинематическую проверку.
Решение. Выбираем симметричную ОС, отбрасывая стержень 11 и заменяя его неизвестной силой  (рис. 24б), определяемой из канонического уравнения
(рис. 24б), определяемой из канонического уравнения 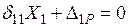 . Коэффициент податливости
. Коэффициент податливости 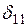 и свободный член
и свободный член 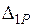 определяются по формулам
определяются по формулам
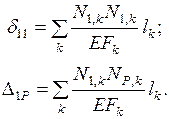 (8.4) Так как модули упругости
(8.4) Так как модули упругости 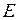 всех стержней одинаковы и площади поперечных сечений
всех стержней одинаковы и площади поперечных сечений 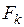 выражены через площадь
выражены через площадь 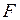 , то вместо (8.4) удобнее использовать выражения
, то вместо (8.4) удобнее использовать выражения
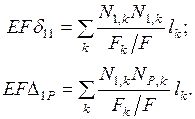 (8.5)
(8.5)
Учитывая, что выбранная ОС является симметричной, суммы в последних выражениях берем только для одной половины, включая стержни 9 и 11, расположенные на оси симметрии (при расчете длины этих стержней уменьшаем вдвое).
Предварительно найдем значения углов 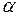 и
и 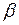 (рис. 24а), необходимые для дальнейших расчетов:
(рис. 24а), необходимые для дальнейших расчетов:
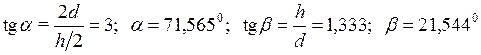 .
.
Для определения сил 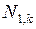 и
и 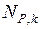 , возникающих в ОС соответственно от сил
, возникающих в ОС соответственно от сил 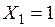 и заданной нагрузки, используем метод вырезания узлов (в расчетах индексы 1 и P опущены).
и заданной нагрузки, используем метод вырезания узлов (в расчетах индексы 1 и P опущены).
Расчет ОС от сил 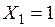 . Так как силы
. Так как силы 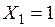 уравновешены, то реакции опор от этих сил отсутствуют. Вырезаем последовательны узлы ОС (рис. 25) и составляем для них уравнения равновесия.
уравновешены, то реакции опор от этих сил отсутствуют. Вырезаем последовательны узлы ОС (рис. 25) и составляем для них уравнения равновесия.
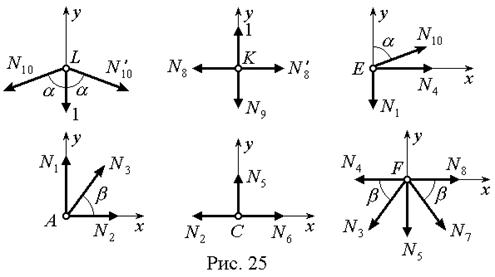
Узел L: 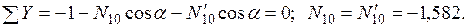
Узел K: 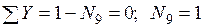 .
.
Узел E: 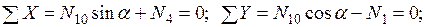
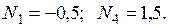
Узел A: 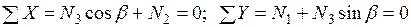 .
.
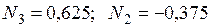 .
.
Узел C: 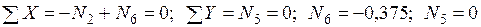 .
.
Узел F: 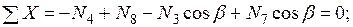
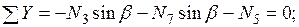
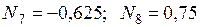 .
.
В стержне 11 от сил 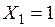
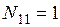 .
.
Расчет ОС от нагрузки. Определяем реакции опор: 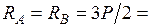
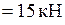 . Из равновесия узлов L, E и K следует:
. Из равновесия узлов L, E и K следует: 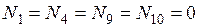 .
.
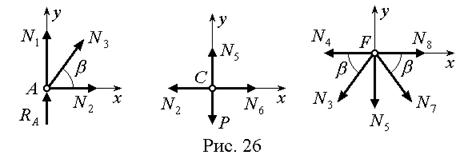
Составляем уравнения равновесия узлов A, C и F (рис. 26).
Узел A: 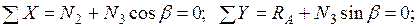
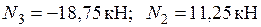 .
.
Узел C: 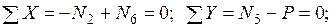
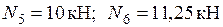 .
.
Узел F: 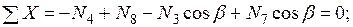
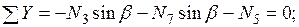
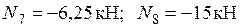 .
.
Вычисляем суммы в правых частях (8.5) Из канонического уравнения находим неизвестную силу: 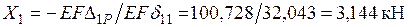 .
.
Окончательные значения сил 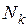 в стержнях фермы определяем по формуле
в стержнях фермы определяем по формуле 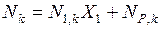 . Расчеты сведены в табл. 13.
. Расчеты сведены в табл. 13.
Таблица 13
| № ст. | l k | Fk / F | N 1, k | N P,k | 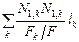
| 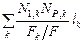
| Nk | 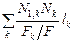
|
| 4,0 | 1,2 | -0,5 | 0,0 | 0,833 | 0,0 | -1,572 | 2,619 | |
| 3,0 | 1,5 | -0,375 | 11,25 | 0,281 | -8,442 | 10,071 | -7,557 | |
| 5,0 | 1,2 | 0,625 | -18,75 | 1,627 | -48,809 | -16,875 | -43,928 | |
| 3,0 | 1,8 | 1,5 | 0,0 | 3,753 | 0,0 | 4,715 | 11,797 | |
| 4,0 | 1,2 | 0,0 | 10,0 | 0,0 | 0,0 | 10,0 | 0,0 | |
| 3,0 | 1,5 | -0,375 | 11,25 | 0,281 | -8,442 | 10,071 | -7,557 | |
| 5,0 | 1,2 | -0,625 | 6,25 | 1,627 | -16,270 | 4,285 | -11,154 | |
| 3,0 | 1,8 | 0,75 | -15,0 | 0,938 | -18,765 | -12,642 | -15,815 | |
| 2,0 | 1,2 | 1,0 | 0,0 | 1,667 | 0,0 | 3,144 | 5,238 | |
| 6,325 | 0,8 | -1,582 | 0,0 | 19,787 | 0,0 | -4,973 | 62,201 | |
| 1,0 | 0,8 | 1,0 | 0,0 | 1,25 | 0,0 | 3,144 | 3,930 | |
| Σ | - | - | - | - | 32,043 | -100,728 | - | -0,226 |
Кинематическая проверка: 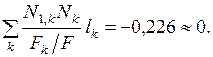
Задание 9. Расчет статически неопределимой рамы методом перемещений
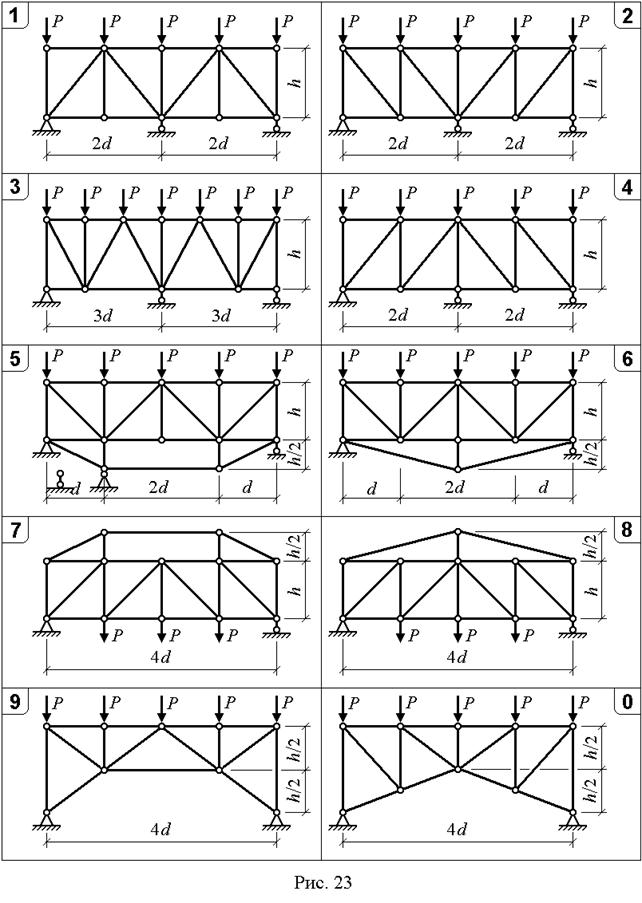
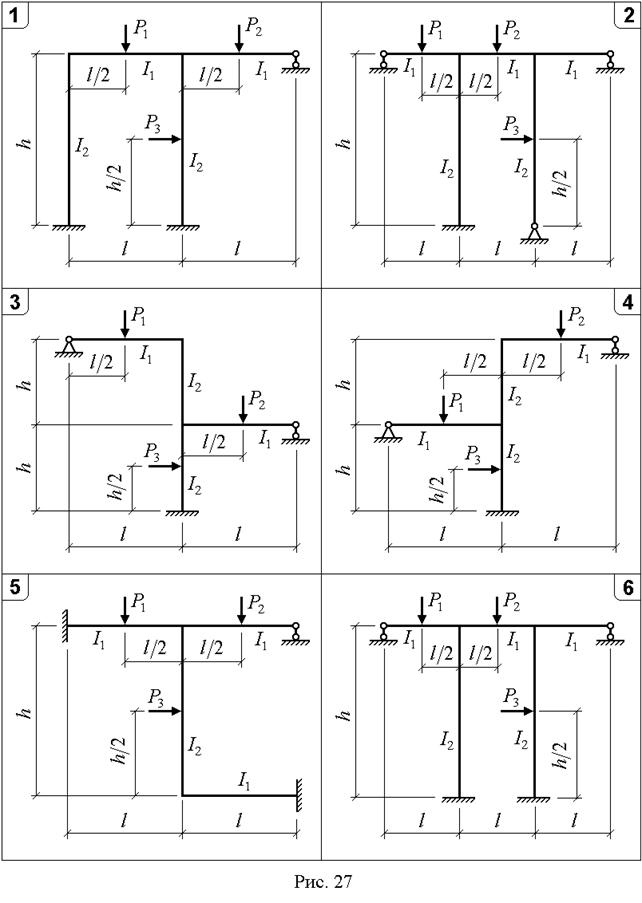
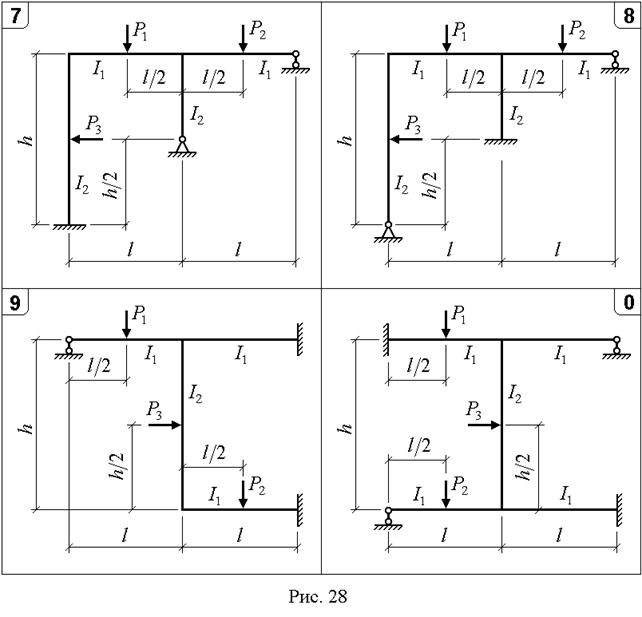
Для заданной статически неопределимой рамы (рис. 27,28) с выбранными по шифру из табл. 14 размерами и нагрузкой требуется: а) построить эпюры  ; б) выполнить статическую проверку.
; б) выполнить статическую проверку.
Таблица 14
| Первая цифра шифра | ||||||||||
| l, м | ||||||||||
| Вторая цифра шифра | ||||||||||
| h, м | ||||||||||
| P 1, кН | ||||||||||
| P 2, кН | ||||||||||
| P 3, кН | ||||||||||
| Третья цифра шифра (№ схемы) | ||||||||||
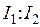
| 1:2 | 2:1 | 2:3 | 3:2 | 1:3 | 3:1 | 3:4 | 4:3 | 4:1 | 1:4 |
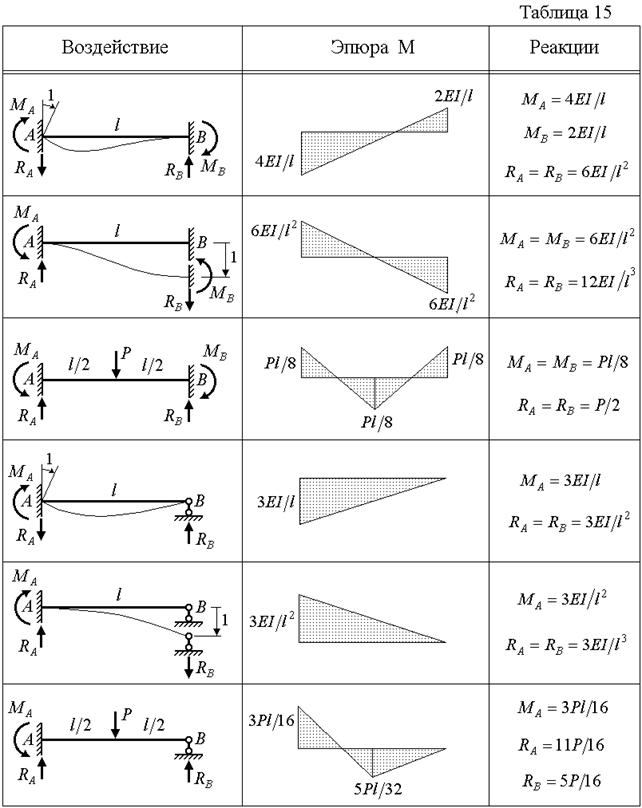
Методические указания. Расчет статически неопределимой рамы методом перемещений осуществляется с помощью основной системы (ОС), которая получается из заданной путем введения дополнительных связей, исключающих линейные перемещения и углы поворота узлов (последние вводятся только в жесткие узлы). Для построения в ОС эпюр 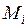 от перемещений и углов поворота
от перемещений и углов поворота 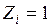 , а также эпюры
, а также эпюры  от нагрузки используются справочные данные, приведенные в табл. 15. Коэффициенты при неизвестных и свободные члены канонических уравнений определяются из равновесия узлов или частей ОС, содержащих дополнительные связи.
от нагрузки используются справочные данные, приведенные в табл. 15. Коэффициенты при неизвестных и свободные члены канонических уравнений определяются из равновесия узлов или частей ОС, содержащих дополнительные связи.
После определения неизвестных 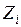 строятся эпюры
строятся эпюры 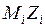 . Окончательная эпюра изгибающих моментов строится в заданной системе с помощью выражения
. Окончательная эпюра изгибающих моментов строится в заданной системе с помощью выражения 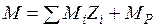 . Эпюра
. Эпюра  на каждом участке строится по эпюре
на каждом участке строится по эпюре 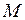 . При отсутствии на участке распределенной нагрузки поперечная сила на нем постоянна и определяется по формуле
. При отсутствии на участке распределенной нагрузки поперечная сила на нем постоянна и определяется по формуле 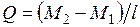 , где
, где 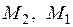 - изгибающие моменты соответственно на правом (верхнем) и левом (нижнем) концах участка. Моменты
- изгибающие моменты соответственно на правом (верхнем) и левом (нижнем) концах участка. Моменты 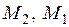 подставляются в формулу с учетом их знаков (
подставляются в формулу с учетом их знаков (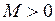 растягивает ригели с нижней, стойки - с правой стороны). Продольные силы
растягивает ригели с нижней, стойки - с правой стороны). Продольные силы 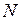 в стержнях определяются по известным значениям
в стержнях определяются по известным значениям  из условий равновесия узлов. При этом
из условий равновесия узлов. При этом 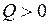 должна поворачивать рассматриваемый узел по часовой стрелке,
должна поворачивать рассматриваемый узел по часовой стрелке, 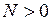 направляется от узла.
направляется от узла.
Проверка равновесия рамы осуществляется тремя уравнениями: 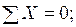
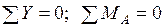 (сумму моментов можно составлять относительно любой точки). Необходимые для этого реакции опор определяются из условий равновесия обобщенных внутренних и внешних сил в опорных узлах.
(сумму моментов можно составлять относительно любой точки). Необходимые для этого реакции опор определяются из условий равновесия обобщенных внутренних и внешних сил в опорных узлах.
Пример выполнения задания. Дано: схема рамы (рис. 29а); 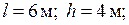
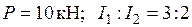 . Требуется: а) построить эпюры
. Требуется: а) построить эпюры  ; б) выполнить статическую проверку.
; б) выполнить статическую проверку.
Решение. Заданная рама имеет два неизвестных угла поворота жестких узлов и одно неизвестное вертикальное перемещение этих узлов. Основную систему метода перемещений получаем из заданной системы путем введения в нее трех дополнительных связей: двух заделок и одного стержня (рис. 29б). Неизвестные углы поворота 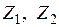 и перемещение
и перемещение 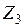 в направлениях дополнительных связей определяются из канонических уравнений
в направлениях дополнительных связей определяются из канонических уравнений
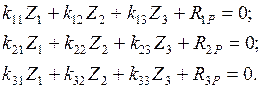
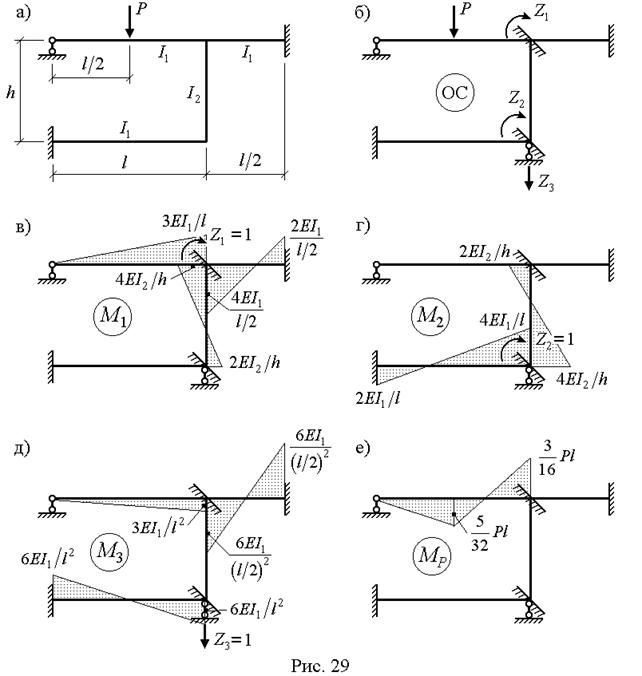
С помощью справочных данных (табл. 15) строим в ОС единичные и грузовую эпюры (рис. 29в, 29г, 29д, 29е). Коэффициенты при неизвестных и свободные члены канонических уравнений определяются из равновесия узлов ОС, содержащих дополнительные связи (рис. 30) с учетом заданного отношения 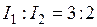 (
(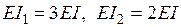 ):
):
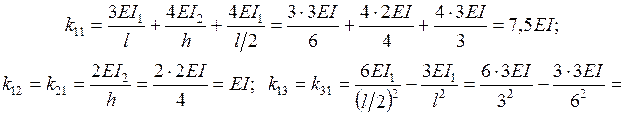
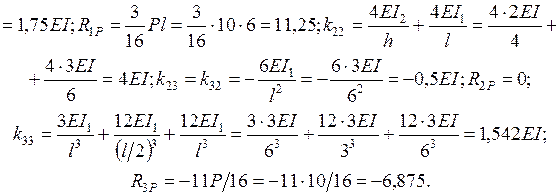

Подставляя эти значения в канонические уравнения и решая последние, получаем: 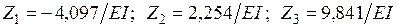 . Строим в ОС эпюры
. Строим в ОС эпюры 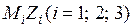 от перемещений
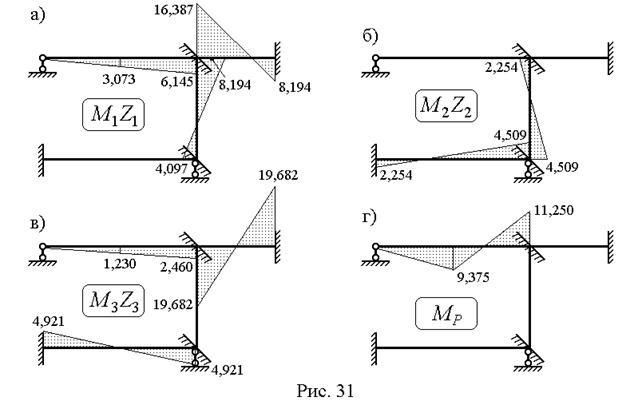
от перемещений 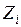 (рис. 31а, 31б, 31в). Окончательная эпюра
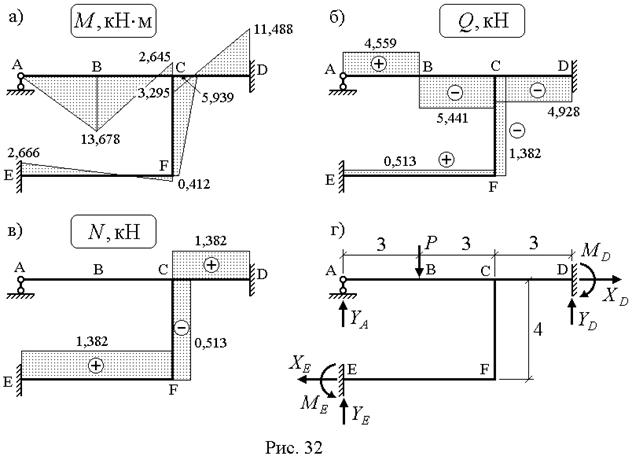
(рис. 31а, 31б, 31в). Окончательная эпюра 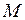 (рис. 32а) получается с помощью выражения:
(рис. 32а) получается с помощью выражения: 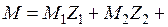
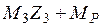 . Проверяем равновесие моментов в узле С:
. Проверяем равновесие моментов в узле С: 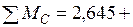
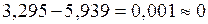 .
.
Поперечные силы на каждом участке определяются по эпюре 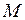 .
.
Участок AB: 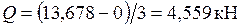 .
.
Участок BC: 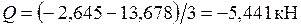 .
.
Участок CD: 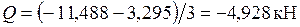 .
.
Участок CF: 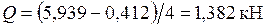 .
.
Участок EF: 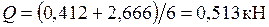 .
.
По полученным на участках значениям поперечных сил строим эпюру  (рис.32б).
(рис.32б).
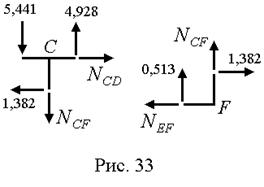
Продольные силы определяем из условия равновесия узлов (рис. 33).
Узел C: 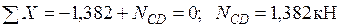 .
.
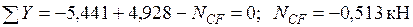 .
.
Узел F: 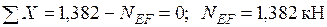 .
.
По полученным значениям строим эпюру 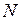 (рис. 32в).
(рис. 32в).
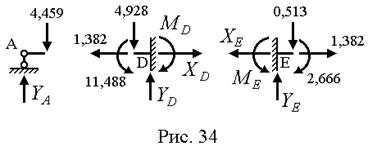
Определяем реакции опор, рассматривая равновесие опорных узлов (рис. 34):
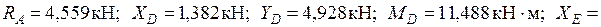
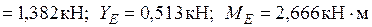 .
.
Проверяем равновесие рамы (рис. 32г):
Литература
1. Дарков А.В., Шапошников Н.Н. Строительная механика. - М.: Высш. шк., 1986.
2. Смирнов В.А., Иванов С.А., Тихонов М.А. Строительная механика. - М.: Стройиздат, 1984.
3. Руководство к практическим занятиям по курсу строительной механики (статически определимые и статически неопределимые системы) / под общ. ред. Г.К. Клейна. - М.: Высш. шк., 1973.
|
|
|
|
|
Дата добавления: 2014-11-25; Просмотров: 652; Нарушение авторских прав?; Мы поможем в написании вашей работы!