
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Определим интервалы вогнутости и выпуклости графика функции
|
|
|
|
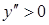 при
при 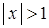 и
и 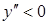 при
при 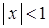 .
.
Таким образом, на интервалах  и
и 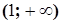 функция имеет вогнутость (
функция имеет вогнутость (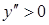 ), а на интервале
), а на интервале  – выпуклость (
– выпуклость (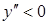 ).
).
7) По полученным данным строим эскиз графика (рис.1).
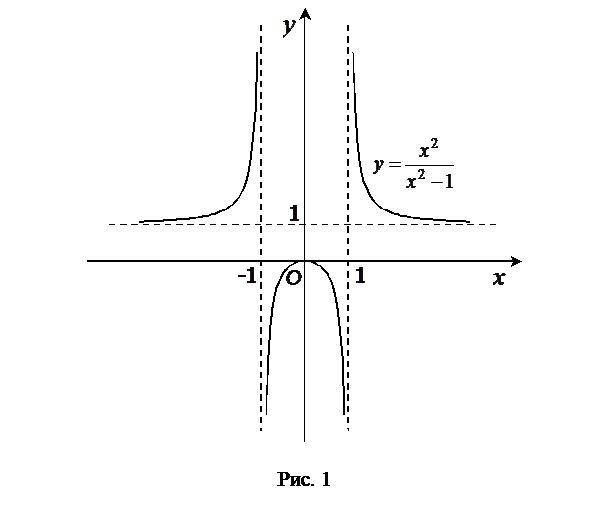
Провести исследование функции и построить ее график:
6.1. 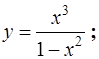
| 6.2. 
|
6.3. 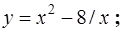
| 6.4. 
|
6.5. 
| 6.6. 
|
6.7. 
| 6.8. 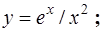
|
6.9. 
| 6.10. 
|
6.11. 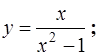
| 6.12. 
|
6.13. 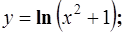
| 6.14. 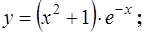
|
6.15. 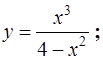
| 6.16. 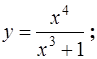
|
6.17. 
| 6.18. 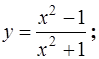
|
6.19. 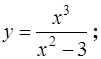
| 6.20. 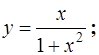
|
6.21. 
| 6.22. 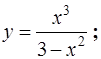
|
6.23. 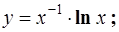
| 6.24. 
|
6.25. 
|
ЗАДАНИЕ 7
Пример: Проволокой длиной l требуется огородить территорию, имеющую форму кругового сектора. Какой следует взять радиус круга, чтобы площадь огороженной территории была наибольшей?
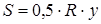 . Исследуем функцию S, зависящую от двух переменных R и y, на максимум. Для этого выразим y через R (можно наоборот). Согласно условию задачи, периметр кругового сектора равен l, т.е.
. Исследуем функцию S, зависящую от двух переменных R и y, на максимум. Для этого выразим y через R (можно наоборот). Согласно условию задачи, периметр кругового сектора равен l, т.е. 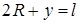 (уравнение связи). Отсюда
(уравнение связи). Отсюда 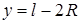 . Следовательно,
. Следовательно,
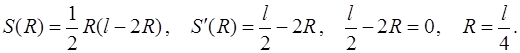
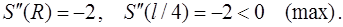
7.1. Требуется изготовить из жести ведро цилиндрической формы без крышки данного объема V. Каковы должны быть высота ведра и радиус его дна, чтобы на изготовление ведра ушло наименьшее количество жести?
7.2. Данное положительное число b разложить на два слагаемых так, чтобы их произведение было наибольшим.
7.3. Открытый бассейн с квадратным дном имеет объем 32 м3. При каких размерах бассейна на облицовку его стен и дна понадобится наименьшее количество материала?
7.4. Прямой круговой конус с наибольшим объемом вписан в данный конус, причем вершина внутреннего конуса находится в центре основания данного конуса. Показать, что высота внутреннего конуса составляет 1/3 высоты данного конуса.
7.5. В сегмент параболы 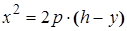 , расположенный над осью OX, вписать прямоугольник с основанием на оси абсцисс наибольшей площади.
, расположенный над осью OX, вписать прямоугольник с основанием на оси абсцисс наибольшей площади.
7.6. Доказать, что из всех круговых цилиндров данного объема наименьшую полную поверхность имеет тот, у которого осевое сечение – квадрат.
7.7. Прямоугольник вписан в эллипс с осями 2 a и 2 b. Каковы должны быть стороны прямоугольника, чтобы его площадь была наибольшей?
7.8. Найти высоту конуса наибольшего объема, который можно вписать в шар радиуса R.
7.9. Из трех досок одинаковой величины сколачивают желоб. При каком угле наклона боковых стенок площадь поперечного сечения желоба будет наибольшей?
7.10. Кусок проволоки длиной l согнуть в виде прямоугольника так, чтобы площадь последнего была наибольшей.
7.11.
7.12. Доказать, что конический шатер данной вместимости требует наименьшего количества материала, когда его высота в  раз больше радиуса основания.
раз больше радиуса основания.
7.13. Какой из прямоугольных треугольников с заданным периметром 2p имеет наибольшую площадь?
7.14. Доказать, что из всех цилиндров, вписанных в данный конус, наибольший объем имеет тот, высота которого равна 1/3 высоты конуса.
7.15. Решеткой длиной l нужно огородить к дому прямоугольную площадку наибольшей площади. Определить размеры прямоугольной площадки.
7.16. Доказать, что из всех трапеций, имеющих три равные данные стороны, наибольшую площадь имеет та трапеция, у которой угол при основании равен π/3.
7.17. Требуется изготовить коническую воронку с образующей, равной h. Какова должна быть высота воронки, чтобы объем ее был наибольшим?
7.18. Сечение тоннеля имеет форму прямоугольника, завершенного полукругом. Периметр сечения p. При каком радиусе полукруга площадь сечения будет наибольшей?
7.19. Из всех конусов, которые можно получить вращением прямоугольных треугольников с гипотенузой b вокруг одного из катетов, найти тот, объем которого будет наибольшим.
7.20. Найти высоту цилиндра наибольшего объема, который можно вписать в шар данного радиуса R.
7.21. По данной сумме двух сторон треугольника и углу, заключенному между ними, образовать треугольник наибольшей площади.
7.22. Найти наибольший объем цилиндра, у которого полная поверхность равна S.
7.23. Найти прямоугольный треугольник наибольшей площади, если сумма катета и гипотенузы его постоянна и равна А.
7.24. Из круглого железного диска радиуса R требуется сделать конус наибольшего объема. Каким должен быть радиус основания этого конуса?
7.25.
|
|
|
|
|
Дата добавления: 2014-11-25; Просмотров: 1345; Нарушение авторских прав?; Мы поможем в написании вашей работы!