Методика определения доверительного интервала для определения истинного значения определяемой величины

Сплошное обследование всех элементов генеральной совокупности может потребовать больших затрат средств и времени. По этой причине исследователь всегда имеет дело с выборочной статистической совокупностью, то есть с частью общей генеральной совокупности.

Однако исследователя прежде всего интересуют свойства всей генеральной совокупности. Поэтому одна из важнейших задач математической статистики заключается в определении параметров всей генеральной совокупности на основании информации, которую можно извлечь из ограниченной выборки. Поясним сказанное примером. Пусть нас интересует среднее время развертывания насосно-рукавной системы для забора воды насосной установкой мобильного средства пожаротушения расчетом из двух человек какого либо гарнизона пожарной охраны. Мы, конечно, можем провести прием зачетов от исполнителей в каждом карауле всех пожарных частей этого гарнизона пожарной охраны и таким образом совершенно точно найти среднее время развертывания двумя исполнителями заранее оговоренных условиях – генеральное среднее M_y.

Однако такое сплошное обследование всей генеральной совокупности потребует больших затрат средств и времени. Поэтому в практике применяют выборочный метод, с помощью этого метода среднее время находят не по всем караулам - всей генеральной совокупности, а по их небольшой части - выборке.

Допустим, для простоты, что весь гарнизон состоит из девяти пожарных частей, которые при развертывания насосно-рукавной системы для забора воды из водоисточника показали следующие результаты 40, 32, 50, 46, 26, 30, 22, 36 и 48 с. Легко подсчитать, что генеральное среднее М_у этой статистической совокупности равно 36,6 с.

Проведем теперь выборочное измерение времени выполнения упражнения по трем произвольно взятым группам исполнителей. Для этого выберем какие-либо три результата (например, первые три) и найдем их среднее значение ₁:

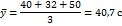
Если бы мы возьмём следующие три измерения - 46, 26, 30, - то получили бы уже другое значение выборочного среднего: ₂ = 34,0 с. В первом случае ошибка - разность между выборочным средним и действительным значением среднего времени - равнялась ₁ -М _у = 40,7- 36,6 = 4,1 с; во втором ₂-М_у = 34,0 -36,6 = - 2,6 с.

Как видим, определение генерального среднего по выборочному производится с ошибкой. Каждое из возможных выборочных значений 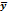(в качестве обследуемых мы могли взять произвольным образом любые три измерения) находится как среднее арифметическое трех случайных величин. Соответственно выборочное среднее также является случайной величиной. Эта случайная величина в ту или иную сторону отклоняется от истинного среднего значения генеральной совокупности.

Точно так же и другие выборочные параметры (например, выборочная дисперсия) являются случайными величинами. Их отклонения от генеральной совокупности случайны. Следовательно, можно указать только вероятность того или иного отклонения и тем самым охарактеризовать численно надежность (достоверность) полученного результата. Вероятность р нахождения истинного значения параметра генеральной совокупности в некоторых пределах называется доверительной вероятностью. Пределы, соответствующие доверительной вероятности, называют доверительными границами, а образуемый ими интервал - доверительным интервалом.

Техника нахождения доверительного интервала для генерального среднего несложна. При выборке объема n < 120 закон распределения ошибки - разности между генеральным и выборочным средним - описывается известной функцией распределения, называемой t -распределением Стьюдента. Используя свойства этого распределения, можно всегда вычислить вероятность отклонения выборочного среднего от генерального на данную величину. Соответственно можно найти и доверительный интервал.

Для расчета доверительного интервала необходимо. Найти выборочное среднее у и оценку дисперсии s². Задаться уровнем значимости q. Уровнем значимости называют вероятность ошибки, которой допустимо пренебречь в данном исследовании. В нашем случае ошибка будет заключаться в том, что генеральное среднее М_у не будет лежать внутри найденного интервала. Поэтому q = 1 -р. Обычно в технологических расчетах величину доверительной вероятности р берут в пределах от 0,9 до 0,99.

Для данного уровня значимости q и числа степеней свободы f = n - 1 из Приложения 4 находят величину t_qf. Расчет доверительного интервала производится по формуле:

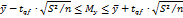
Пример. В результате серии экспериментов из n = 30 испытаний были получены следующие значения: = 28,2 с, S² = 36. Требуется определить доверительные границы для среднего значения, соответствующие 95%-ной доверительной вероятности.

Решение. Для доверительной вероятности р = 0,95 уровень значимости q = 1 - - 0,95 = 0,05. Число степеней свободы f = 30 - 1 = 29. Из Приложения находим для данных значений q и f значение t_qf = 2,04. Подставляя полученные результаты в формулу (8.15), получаем 28,2 - 2,04 1,09 ≤ М_y ≤ 28,2 + 2,04 1,09, или, окончательно, 26,02 ≤ M_y ≤ 30,42.

Таким образом, с вероятностью 0,95 среднее значение заключено между 26,02 с и 30,42 с. То есть из 100 выполненных произвольных экспериментов 95 будут иметь среднее время, лежащее в найденном интервале.

Дата добавления: 2014-11-25