Методика построения интервального вариационного ряда. Частости и накопленные частости

Вариационные ряды – ряды распределения единиц совокупности по признакам, имеющим количественное выражение, т. е. образованы численными значениями.

Вариационные ряды по строению делятся на:

Дискретные (прерывные) – основаны на прерывных вариациях признака. Это такие ряды, где значения вариант имеют значения целых чисел (т. е. не могут принимать дробные значения). Дискретные признаки отличаются друг от друга на некоторую конкретную величину.

Интервальные (непрерывные) – имеют любые, в том числе и дробные количественные выражения и представлены в виде интервалов. Непрерывные признаки могут отличаться один от другого на сколь угодно малую величину.

Вариационные ряды имеют два элемента:

варианта (x)

частота (f)

Варианта – отдельное значение варьируемого признака, которое он принимает в ряду распределения.

Частота – численность отдельных вариант или каждой группы вариационного ряда. В некоторых случаях применяется частость. Частоты, выраженные в % или долях процента, называются частостями и рссчитываются как отношение локальной частоты варианты к сумме накопленных частот.

Накопленная частость- сумма частостей.

Пусть в результате наблюдений или опытов исследователь получил некоторые статистические данные - статистическую совокупность, -чис­ленно характеризующие свойства объекта исследования. Статистические данные могут состоять из длинного ряда сотен и даже тысяч чисел. Чтобы извлечь из них полезную информацию, исследователь должен системати­зировать эти данные, то есть привести их в какой-то порядок. Для этого отдельные наблюдения, совпадающие по величине или не очень отличаю­щиеся друг от друга, объединяют в группы. При этом исследователь отмечает, какое количество наблюдений попадает в ту или иную группу. В результате получается относительно короткий ряд данных, который называется статистическим рядом.

для получения статистического ряда необходимо весь диапазон из­менения случайной величины разделить на к интервалов. Обычно исполь­зуют 10–20 интервалов, а сами интервалы берутся одинаковой длины h. В этом случае длины всех интервалов вычисляют по формуле:

Где у_max и y_min - максимальное и минимальное значения случайных величин выборки, k- количество интервалов.

Далее определяется количество m наблюдений, попавших в каждый i- й интервал. Количество m наблюдений, попавших в какой-либо интервал, называют частотой.

приведен статистический ряд, получившийся в результате группирования 140 замеров временных параметров выполнения одного из видов развертывания насосно-рукавных систем для транспортирования и подачи огнетушащих веществ с использованием насосной установки мобильного средства пожаротушения. Минимальная время 400 с (y_min = 400 с), а максимальная -1300 с (у _max =1300 с). Следовательно, весь диапазон изменения случайных величин выборки равен 1300 - 400 = 900с. Этот диапазон разбит на 18 интервалов, т. е.

длина каждого интервала равна

Количество значений времени заключённых между 400 и 450 с, равняется 4; между 450 и 500 с - 8 и т. д. Как видим, результаты наблюдений, содержащие 140 замеров, удалось при помощи статического ряда представить в компактной и удобной для дальнейшего анализа форме.

Статический ряд можно изображать графиком, который называется гистограммой. Гистограмма состоит из примыкающих друг к другу прямо­угольников, основание которых равно длине интервала h, а высота соответствует числу элементов выборки, попавших в данный интервал.

Результаты 140 временных параметров,с

Частота mi представляет собой количество наблюдений, соответствующих данному наблюдению для дискретной переменной для сгруппированного ряда или число наблюдений, попавших в данный интервал для интервального ряда. Значение соответствующей частоты, деленной на объем выборки характеризует частость попадания xi в частичные интервалы.

19(2) Методика определения количества измерений и интервалов между измерениями при исследовании оперативно – тактических действий.

Определив доверительный интервал, мы тем самым определяем точность, с которой выборочное среднее совпадает с генеральным средним М_у. Можно поставить и обратную задачу: найти такой объем выборки n_р, чтобы вероятность р отклонения выборочного среднего от генерального среднего М_у на величину, большую Δ, была достаточно мала. Надежность полученного таким образом результата (уровень достоверности) будет равна:

p = 1-q

Например, мы хотим, чтобы вероятность отклонения выборочного среднего от генерального среднего М_у = 36,6 с (см. пример из предыдущего пункта) на величину, большую Δ = 3 с, была равна 0,01. Отклонение выборочного среднего от действительного на величину больше 3 с при этих условиях наблюдалось бы только в одном случае из 100. Спрашивается, сколько наблюдений и мы должны произвести, чтобы это условие выполнялось?

Выборка, которая с достаточной точностью представляет параметры генеральной совокупности, называется представительной, или репрезентативной.

Для определения объема репрезентативной выборки предварительно ставится серия наблюдений объемом n. Число n опытов предварительной серии наблюдений определяется априорной информацией о степени изменчивости изучаемой величин (при исследовании оперативно-тактических действий число n рекомендуется брать порядка 50-150).

По результатам серии предварительных опытов необходимо:

Вычислить выборочное среднее и выборочную дисперсию S²;

Найти объем n_р репрезентативной выборки по формуле:

Величина Δ представляет собой абсолютную допускаемую ошибку определения среднего значения выборки. Относительно допускаемая ошибка ε будет равна

Если при определении объема репрезентативной выборки требуется учитывать относительную ошибку, то следует использовать формулу

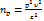
где υ - коэффициент вариации.

Формулы справедливы и в том случае, если объем n серии предварительных опытов невелик (n < 120).

Чтобы проверить, является ли выборка из n_р наблюдений действительно репрезентативной, нужно найти доверительный интервал для выборочного среднего , полученного из этой выборки.

Дата добавления: 2014-11-25