КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Решение задачи о назначениях
|
|
|
|
Пусть имеется 5 видов работ и 5 претендентов для их выполнения, причем каждый претендент может использоваться на любой работе. Известна производительность і -го пре-тендента на j- ой работе (Сij). Требуется так распределить претендентов по работам, чтобы суммарная производительность была максимальной. При этом каждого претендента можно назначить только на одну работу и на каждую работу можно назначить только одного пре-тендента, если:
|
|
|
|
|
|
|
|
è3 2 2 2 6ø
Данная задача относится к задачам транспортного типа, для которой сумма по стро-кам и столбцам равна единице. Математическая модель имеет вид:
|
Z = cijxij ® max i =1 j =1
ìå xij =1ï j =1
n
í xij =1
i =1
ï xij ³ 0, xij Î 0;
|
. (6.1)
|
представлять собой тарифную сетку. План распределения должен состоять только из це-лых чисел {0; 1}. Заметим, что баланс модели здесь не нужен, так как модель состоит только из уравнений-ограничений.
Математическая модель задачи о назначении, внесенная в ячейки электронных таб-лиц Excel, представлена на рисунке ниже (рис.6.1).
Заполняем основное окно Поиска решения и Параметров модели, как для транс-портной задачи линейного программирования (рис.6.2). При этом нет необходимости вво-
 |
дить дополнительное ограничение о бинарном характере переменных.
 |
Рисунок 6.1 Задача о назначении на рабочем листе Excel
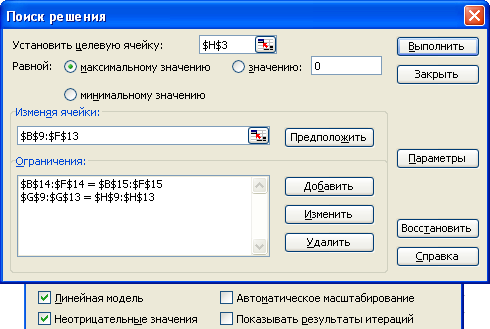Рисунок 6.2 Заполненное диалоговое окно Поиска решения
Нажимаем кнопку Выполнить и получаем следующий результат.
 |
Рисунок 6.3 Результат моделирования назначений
| № вар. | Задачи |
| 4 27 41 | |
| 9 31 51 | |
| 12 21 48 | |
| 1 35 45 | |
| 11 24 54 | |
| 5 40 60 | |
| 7 22 48 | |
| 17 39 44 |
Вариантызаданий
| № вар. | Задачи |
| 1 24 47 | |
| 13 30 52 | |
| 7 34 46 | |
| 10 22 49 | |
| 16 39 52 | |
| 3 28 42 | |
| 14 32 29 | |
| 4 29 55 |
| № вар. | Задачи |
| 10 26 50 | |
| 2 37 47 | |
| 6 28 58 | |
| 14 21 53 | |
| 20 31 57 | |
| 15 25 43 | |
| 11 37 44 |
Задачи 1-20
Решить задачу коммивояжера (рациональной загрузки оборудования)
| ¥ | ||||
| ¥ | ||||
| ¥ | ||||
| ¥ | ||||
| ¥ |
| ¥ | ||||
| ¥ | ||||
| ¥ | ||||
| ¥ | ||||
| ¥ |
| ¥ | |||||
| ¥ | |||||
| ¥ | |||||
| ¥ | |||||
| ¥ | |||||
| ¥ |
| ¥ | |||||
| ¥ | |||||
| ¥ | |||||
| ¥ | |||||
| ¥ | |||||
| ¥ |
| ¥ | |||||
| ¥ | |||||
| ¥ | |||||
| ¥ | |||||
| ¥ | |||||
| ¥ |
Задачи 21-60 Решить задачу о назначении
| ||||
|
|
|
|
|
Дата добавления: 2014-11-25; Просмотров: 446; Нарушение авторских прав?; Мы поможем в написании вашей работы!