Пример моделирования 2 страница

Вариант 18

Изд.1	Изд.2	Изд.3	Запас

Вариант 19

Ресурсы	Изд.1	Изд.2	Изд.3	Запас
Сырье
Оплата
Энергия
Транспорт

Вариант 22

Ресурсы	Изд.1	Изд.2	Изд.3	Запас
Сырье
Оплата
Энергия
Транспорт

Вариант 25

Ресурсы	Изд.1	Изд.2	Изд.3	Запас
Сырье
Оплата
Энергия
Транспорт

Вариант 28

Ресурсы	Изд.1	Изд.2	Изд.3	Запас
Сырье
Оплата
Энергия
Транспорт

Вариант 20

Изд.1	Изд.2	Изд.3	Запас

Вариант 23

Изд.1	Изд.2	Изд.3	Запас

Вариант 26

Изд.1	Изд.2	Изд.3	Запас

Вариант 29

Изд.1	Изд.2	Изд.3	Запас

Вариант 21

Изд.1	Изд.2	Изд.3	Запас

Вариант 24

Изд.1	Изд.2	Изд.3	Запас

Вариант 27

Изд.1	Изд.2	Изд.3	Запас

Вариант 30

Изд.1	Изд.2	Изд.3	Запас

Контрользнаний

1. Сформулируйте исходную и двойственную задачу для модели оптимального распреде-ления ресурсов.

2. Запишите математические модели исходной и двойственной задачи.

3. Назовите правила формирования симметричной пары двойственных задач. 4. Сформулируйте первую терему двойственности.

5. Объясните экономический смысл первой теоремы двойственности.

6. Сформулируйте вторую терему двойственности о дополняющей не жесткости. 7. Объясните экономический смысл второй теоремы двойственности.

8. Что означают переменные двойственной задачи?

9. Где средство Поиск решений отображает результаты решения двойственной задачи? 10.Где средство Поиск решений отображает результаты решения исходной задачи? 11.Как изменение исходных данных может повлиять на результат моделирования?

Лабораторная работа № 5

Тема: Транспортно-распределительнаямодельЦельработы:

ƒ изучение надстройки над таблицами Excel «Транспортное моделирование»;

ƒ формирование математической модели на основании алгоритмических правил; ƒ поиск оптимального транспортного плана.

Времяработы: 4 часа

Задание

1. Решить задачи с помощью надстройки «Транспортное моделирование»; 2. Провести двухэтапное транспортное моделирование.

Транспортнаязадача

Транспортно-распределительная модель по своей сути является транспортной зада-чей, в которой однотипные грузы распределяются по транспортным потокам.

В n пунктах отправления (А 1, А 2, …, Аn), которые в дальнейшем будем называть по-ставщиками, сосредоточено определенное количество некоторого груза или запасов (а 1, а 2, …, аn). Этот груз заказан в m пунктах (В 1, В 2, …, Вт) в количестве, соответствующем по-данным заявкам (b 1, b 2, …, bm). Известны расходы на перевозку единицы продукта из пунк-та Ai в пункт Bj, которые равны Cij и приведены в матрице транспортных расходов.

Требуется составить такой план перевозок, при котором весь продукт вывозится из пунктов Ai в пункты Bj в соответствии с потребностью, а общая величина транспортных издержек будет минимальной.

Математическая модель транспортной задачи имеет вид:

Z = å ci j xi j ® min i j

{ }

ï

ìå xi j £ =³ ai; i =1, n

ï

{ }

å

í

ï

j. (5.1) ï i xij £ =³ bj; j =1, m

î xij ³ 0

До недавнего времени основную проблему в транспортном моделировании состав-ляли неравенства системы ограничений, так как на практике суммы поставок и заявок обычно не совпадают. При этом разрешимость задачи базировалась на теореме.

Теорема. Транспортная задача имеет решение, если сумма заявок равна сумме поставок.

С развитием ЭВМ потребность в соблюдении теоремы отпала, так как появились ал-горитмические правила, на основании которых легко можно получить решение транспорт-ной задачи, например в электронных таблицах Excel.

Алгоритмические правила формирования математической модели:

−меньшая из двух сумм (поставок å ai или заявок å bj) является балансоммодели; i j

− если сумма поставок (заявок) равна балансу модели, то все ограничения по перевозкам для данного поставщика (потребителя) являются уравнениями;

− если сумма поставок (заявок) больше, чем баланс модели, то все ограничения по пере-возкам для данного поставщика (потребителя) являются неравенствами вида «меньше или равно».

В процессе построения математической модели в рамках электронных таблиц следу-ет придерживаться блочной структуры (рис.5.1), которую условно можно разделить на та-рифный (ценовой) модуль и управляемый, основу которого составляют ячейки транспорт-ного плана.

Рассмотрим решение транспортной задачи на конкретном примере. Исходные дан-ные представлены в следующей таблице (табл.5.1)

Таблица 5.1 Исходные данные

а	C
b ®

Блок тарифов

Целевая функция: сумма произведения тарифов и плана

Потребители Bj

Поставщики Аi

План перевозок

Выпол-нение поставок

Фактиче-ские запасы

Выполнение заявок S ai

Фактические заявки S bj

Рисунок 5.1 Блочная структура построения транспортной задачи

Решим предложенную задачу (табл.5.1) с использованием надстройки «Транспорт-ное моделирование». После подключения надстройки (файл Transport 2003-2007) в диало-говых окнах задаем исходные данные. При этом надстройка сама формирует необходимые блоки на рабочем листе Excel. По окончании их формирования появляется основное диа-логовое окно Транспортного моделирования (рис.5.2), в котором выбираем «Стандартную модель» и нажимаем кнопку ОК. После чего программа предложит просмотреть результат моделирования (рис.5.3).

Рисунок 5.2 Диалоговое окно выбора варианта модели

Надстройка «Транспортное моделирование» использует те же алгоритмы, что и По-иск решения. Однако диалоговые окна Поиска решений пользователю для заполнения не предъявляются. Их заполнение идет автоматически самой программой. Например, запол-ненное основное окно Поиска решения представлено на рисунке 5.4. Программа на осно-вании характеристик решаемой задачи сама делает ссылки на нужные ячейки, а некоторые из них объявляет специальными именами, что делает диалоговое окно более читабельным, а период решения задачи на ЭВМ сокращается.

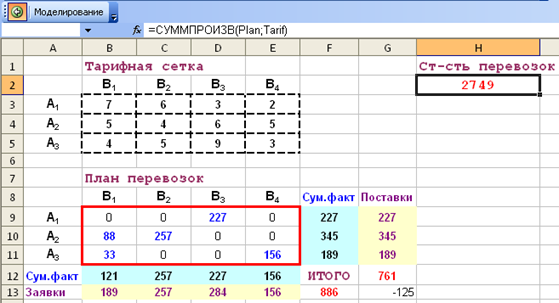Рисунок 5.3 Результат решения транспортной задачи

Рисунок 5.4 Заполненное программой окно Поиска решения

Попробуем другой вариант моделирования. Дополним условия предыдущей задачи ограничениями на пропускную способность. Поставщик А 1 должен поставить потребителю В 1 не менее 50 ед. груза (х 11 => 50), а перевозка от него же (А 1) потребителю В 3 не должна превышать 150 ед. груза (х 13 <= 150).

В основном диалоговом окне Транспортного моделирования отмечаем «Модель с ограничениями пропускной способности» и нажимаем кнопку ОК. Появляется диалоговое окно (рис.5.5), в котором следует указать число ограничений, равное 2.

Рисунок 5.5 Окно числа ограничений

Затем появляется диалоговое окно, в котором следует записать адрес блокируемой ячейки. Например, в данном примере это ячейка В9 (запись легче всего выполнить с по-мощью указателя «мышь»). Далее идут диалоговые окна с указателями по направлению ограничения и предполагаемыми значениями границ (рис.5.6).

Рисунок 5.6 Ввод предельного значения

Получаем следующий результат моделирования (рис.5.7).

Рисунок 5.7 Результат моделирования с ограничениями

Двухэтапнаятранспортнаязадача

Двухэтапная транспортная модель отличается от ранее рассмотренной транспортной задачи тем, что в ней есть промежуточное звено, называемое складами Dk. По сути, эта мо-дель включает в себя две задачи по составлению плана перевозок: от поставщика на склад и со склада – потребителям. В принципе возможно решение каждой задачи, как самостоя-тельной, но тогда может появиться увеличение стоимости перевозок по причине того, что направления с минимальным тарифом для склада в направлении от поставщика не совпа-дают с минимальными тарифами по направлению к потребителям. Поэтому обе задачи ре-комендуют решать, как единую модель, которая является двухэтапной транспортной зада-чей.

При построении модели делается ряд предположений: − товар является однородным;

− товар является делимым, т.е. может перевозиться партиями любого размера;

− свойства товара не меняются во времени, т.е. рассматривается статическая модель: время в явном виде в нее не входит. Данное предположение означает, что, во-первых, предложения, спросы и емкости складов являются интегральными характе-ристиками за некоторый период времени (год, квартал или месяц), а во-вторых, пе-ревозки также интегральные и осуществляются "мгновенно";

− все поставщики связаны коммуникациями со всеми складами, а последние, в свою

очередь, со всеми потребителями;

í ý

î þ

− суммарная емкость складов всегда превышает наибольшую сумму из поданных зая-вок или поставок å dk ³maxìå ai;å bj ü.

k i j

}

{ }

− затраты на перевозки прямо пропорциональны объемам перевозок и известны та-рифы – стоимости перевозок единицы товара. Тарифы образуют две матрицы

* *

C = cik и C *= ckj, где cik и ckj – стоимости перевозки единицы товара от Ai к Dk и от Dk к Bj.

Поставщики

Ai cik

Блок тарифов

не перевозку

Значение функции цели

склады dk Z

0 склады 0

dk 0 0

Потребители

c*kj Bj

Рисунок 5.8 Блочная структура двухэтапной транспортной задачи

Блочная структурная схема двухэтапной транспортной задачи для электронных таб-лиц Excel по принципу построения аналогична структуре обычной транспортной задачи. Она также состоит из блока тарифов и блока перевозок. Однако каждый в свою очередь делится на три компонента:

– перевозка от поставщика на склад;

– свободное место Vk внутри складских помещений (остатки объема); – перевозка со склада потребителям.

Рассмотрим конкретный пример двухэтапной транспортной задачи.

Запасы поставщиков, ёмкости складов и заявки потребителей, а также тарифы пере-возок от поставщика на склад (Аi ® Dk) и со склада потребителям (Dk ® Bj) даны в таблице.

Таблица 5.2 Исходные данные

а	b	d	C (Аi ® Dk)	C (Dk ® Bj)
			2 4 3 3 1 2 4 2 3	12 11 8 10 14 11 7 12 10

Необходимо составить оптимальный план перевозок.

Сумма поставок составляет ai =650, заявок – å bj =550, емкость складов – å dk =800. Минимальной является сумма заявок – это баланс модели. Поэтому:

− сумма грузов, доставляемых потребителю, равна значению, указанному в заявке å x * ik = bj, j =1, m;

k

− сумма грузов перевозимых от поставщика на склад не превышает его запасы å xjk £ ai, i =1, n;

k

−для складов рассматриваются уравнения xik + Vk = d и å x * kj + Vk = dk. k k

Заполняем ячейки рабочего листа электронных таблиц Excel исходными данными и формульными зависимостями. Расстановку блоков задачи выполняем в соответствии с об-щепринятой структурой построения модели (рис.5.8), дополняя ее необходимыми подпи-сями и форматируя ячейки электронных таблиц таким образом, чтобы результат решения легко читался. Следует заметить, что инструмент Автосумма способен фильтровать числа, отделяя их от текстовых записей в промежуточных ячейках. Например, для формула ячей-ки Н13: =СУММ(B13:G13); или для ячейки, в которой подсчитывается функция цели – I3: =СУММПРОИЗВ(B3:G8;B11:G16).

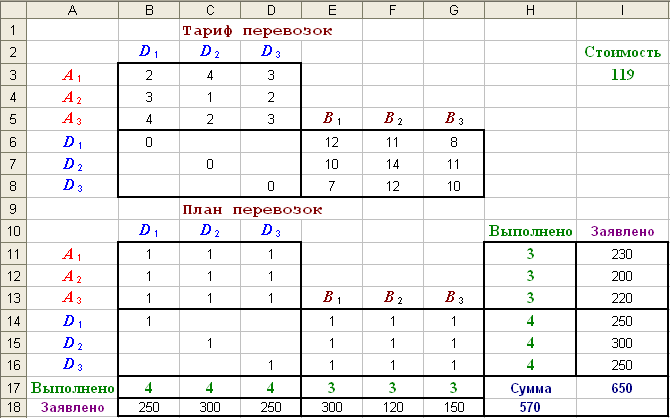Рисунок 5.9 Построение двухэтапной транспортной задачи в Excel

Переходим к заполнению основного окна Поиска решения. Здесь в качестве управ-ляемых переменных рассматриваются следующие диапазоны ячеек и отдельные ячейки1:

Дата добавления: 2014-11-25