Отношения между суждениями

Условные, разделительные и лемматические дедуктивные умозаключения.

Чисто условное умозаключение-умозаключение в котором все посылки и заключения условные суждения

Структура: если m то p

Если n то p

…................если m то р

Разделительно-категорическим называется умозак­лючение, в котором одна из посылок — разделительное, а другая посылка и заключение — категорические суждения.

Простые суждения, из которых состоит разделительное (дизъюнктивное) суждение, называются членами дизъюнк­ции, или дизъюнктами. Например, разделительное суждение «Облигации могут быть предъявительскими или именными» состо­ит из двух суждений — дизъюнктов: «Облигации могут быть предъявительскими» и «Облигации могут быть именными», соеди­ненных логическим союзом «или».

Утверждая один член дизъюнкции, мы с необходимостью должны отрицать другой и, отрицая один из них, — утверждать другой. В соответствии с этим различают два модуса разделительно-категорического умозаключения: утверждающе-отрицающий и отрицающеутверждающий.

● В утверждающе-отрицающем модусе (modus ponendo tollens) меньшая посылка, категорическое суждение, утверждает один член дизъюнкции, заключение — также категорическое суждение — отрицает другой ее член. Например:

Облигации могут быть предъявительскими (р) или именными (q).

Данная облигация предъявительская (р).

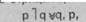Данная облигация не является именной (q).

Схема утверждающе-отрицающего модуса →

V — символ строгой дизъюнкции.

Заключение по этому модусу всегда достоверно, если соблюдается правило: большая посылка должна быть исключающее-разделительным суждением, или суждением строгой дизъюн­кции. Если это правило не соблюдается, достоверного заключе­ния получить нельзя. В самом деле, из посылок «Кражу совершил К. или Л.» и «Кража совершена К.» заключение «Л. кражу не совер­шал» с необходимостью не следует. Возможно, что Л. также при-частен к совершению кражи, является соучастником К.

● В отрицающе-утверждающем модусе (modus tollendo ponens) меньшая посылка отрицает один дизъюнкт, заключение утверждает другой. Например:

Облигации могут быть предъявительскими (р) или именными (q).

Данная облигация не является предъявительской (1 р).

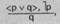Данная облигация именная (q).

Схема отрицающе-утверждающего модуса →

< > — символ закрытой дизъюнкции.

Утвердительный вывод получен посредством отрицания: отри­цая один дизъюнкт, мы утверждаем другой. Заключение по этому модусу всегда достоверно, если соблюдается правило: в большей посылке должны быть перечис­лены все возможные суждения — дизъюнкты, иначе говоря, боль­шая посылка должна быть полным (закрытым) дизъюнктивным высказыванием. Применяя неполное (открытое) дизъюнктивное высказывание, достоверного заключения получить нельзя.

Условно-разделительный силлогизм. Умозаключение, в котором одна посылка условное, а другая — разделительное суждения, называется условно-разделительным, или лемматическим (от лат. — предположе­ние). Разделительное суждение может содержать две, три и боль­шее число альтернатив, поэтому лемматические умозаключения делятся на дилеммы (две альтернативы), трилеммы (три альтер­нативы) и т.д.

Рассмотрим на примере дилеммы структуру и виды условно-разделительного умозаключения. Различают два вида дилемм: конструктивную (созидательную) и деструктивную (разрушитель­ную), каждая из которых делится на простую и сложную.

Модусы: утверждающий –отрицающий и отрицающее-утверждающий В простой конструктивной дилемме условная посылка содержит два основания, из которых вытекает одно и то же след­ствие. Разделительная посылка утверждает оба возможных осно­вания, заключение утверждает следствие. Рассуждение направле­но от утверждения истинности оснований к утверждению истинно­сти следствия.

Схема простой конструктивной дилеммы:

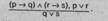
Если обвиняемый виновен в заведомо незаконном задержа­нии (р), то он подлежит уголовной ответственности за преступле­ние против правосудия (г); если он виновен в заведомо незакон­ном заключении под стражу (q), то он также подлежит уголовной ответственности за преступление против правосудия (г).

Обвиняемый виновен или в заведомо незаконном задержа­нии (р) или в заведомо незаконном заключении под стражу (q).

Обвиняемый подлежит уголовной ответственности за преступ­ление против правосудия (г).

В сложной конструктивной дилемме условная посылка содержит два основания и два следствия. Разделительная посылка утверждает оба возможных следствия. Рассуждение направлено от утверждения истинности оснований к утверждению истиннос­ти следствий.

Схема сложной конструктивной дилеммы:

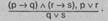
В простой деструктивной дилемме условная посылка со­держит одно основание, из которого вытекает два возможных следствия. Разделительная посылка отрицает оба следствия, зак­лючение отрицает основание. Рассуждение направлено от отри­цания истинности следствий к отрицанию истинности основания.

Схема простой деструктивной дилеммы:

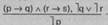
Если Н. совершил умышленное преступление (р), значит, в его действиях был прямой (q) или косвенный умысел (г).

Но в действиях Н. не было ни прямого (q), ни косвенного умысла (г).

Преступление, совершенное Н., не является умышленным (р).

В сложной деструктивной дилемме условная посылка со­держит два основания и два следствия. Разделительная посылка отрицает оба следствия, заключение отрицает оба основания. Рассуждение направлено от отрицания истинности следствий к отрицанию истинности оснований.

Схема сложной деструктивной дилеммы:

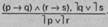
Если предприятие является арендным (р), то оно осуществляет предпринимательскую деятельность на основе взятого им в арен­ду имущественного комплекса (q); если оно является коллектив­ным (г), то осуществляет такую деятельность на основе находяще­гося в его собственности имущества (s).

Данное предприятие не осуществляет свою деятельность ни на основе взятого в аренду имущественного комплекса (1 а), ни на основе находящегося в его собственности имущества (Is).

Данное предприятие не арендное (1 р) или не коллективное (1 г).

10. Логические операции с простыми суждениями:превращение, обращение,противопоставление

Логические операции с суждениями затрагивают их типы и виды, их субъектно-предикатную структуру и т. д. Среди данных операций выделяют две наиболее общие и важные группы: преобразование простых и сложных суждений и отрицание данных суждений.

Преобразование суждений – выяснение точного логического смысла суждения. Это достигается посредством таких логических операций, как обращение, превращение, противопоставление субъекту и противопоставление предикату.

Обращение – это непосредственное умозаключение, состоящее в преобразовании категорического суждения в такое суждение, субъектом которого является предикат исходного, а предикатом – субъект исходного суждения.

Другими словами, при выводе с помощью обращения субъект и предикат меняются местами. При этом в случае, когда исходным суждением (посылкой) является общеутвердительное суждение, меняется также количество суждения, то есть заключение становится частным. Такое обращение называется «обращением с ограничением» или «чистым обращением».

Формы выводов с помощью обращения:

1) для общеутвердительного суждения:
Все S есть Р.
Некоторые Р есть S.

2) для общеотрицательного суждения:
Ни одно S не есть Р.
Ни одно Р не есть S.

3) для частноутвердительного суждения:
Некоторые S есть Р.
Некоторые Р не есть S.

4) для частноотрицательного суждения путём обращения нельзя логически правильно вывести какое-либо заключение, так как в этом случае нарушается общее правило выводов из категорических суждений: термин, не распределённый в посылках, не должен быть распределён в заключении.

Превращение (обверсия) – это преобразование суждения путем перемены его качества на противоположное. Количество суждения, его субъект и предикат при этом не меняются. Например: «Все адвокаты – юристы». Посредством превращения данное суждение преобразовывается в следующее: «Ни один адвокат не является неюристом».

Другими словами, при выводе с помощью превращения отрицательное суждение преобразуется в утвердительное и, наоборот, утвердительное – в отрицательное, а предикат берётся с отрицанием (то есть Р меняется на не-Р или не-Р на Р).

Формы выводов с помощью превращения:

1) для общеутвердительного суждения:
Все S есть Р.
Ни одно S не есть не-Р.

2) для общеотрицательного суждения:
Ни одно S не есть Р.
Все S есть не-Р.

3) для частноутвердительного суждения:
Некоторые S есть Р.
Некоторые S не есть не-Р.

4) для частноотрицательного суждения:
Некоторые S не есть Р.
Некоторые S есть не-Р.

Противопоставление предикату - это преобразование категорического суждения, в результате которого субъектом становится понятие, противоречащее предикату, а предикатом - субъект исходного суждения.

Такой вывод можно сделать, последовательно применяя превращение исходного суждения и далее обращение полученного при этом суждения либо следуя правилам для противопоставления предикату:

1) для общеутвердительного суждения:
Все S есть Р.
Ни одно не-Р не есть S.

2) для общеотрицательного суждения:
Ни одно S не есть Р.
Некоторые не-Р есть S.

3) для частноотрицательного суждения:

Некоторые S не есть Р.

Некоторые не-Р есть S.

4) для частноутвердительных суждений нельзя проводить вывод путем противопоставления предикату, так как после превращения исходного суждения получается частноотрицательное суждение, для которого не применяется операция обращения.

Пример. Противопоставление предикату для частноотрицательного суждения «Некоторые озера не имеют стока»:

Некоторые водоемы, являющиеся озерами (^ S),
не есть водоемы, имеющие сток (Р).

Некоторые водоемы, не имеющие стока (не-Р),
есть водоемы, являющиеся озерами (S).

Противопоставление субъекту - это преобразование категорического суждения, в результате которого субъектом становится предикат исходного суждения, а предикатом - понятие, противоречащее субъекту исходного суждения.

Такой вывод можно осуществить, последовательно применяя обращение исходного суждения, а затем - превращение полученного результата, либо сразу следуя правилам для противопоставления субъекту:

1) для общеутвердительного суждения:
Все S есть Р.
Некоторые Р не есть не-S.

2) для общеотрицательного суждения:
Ни одно S не есть Р.
Все Р есть не-S.

3) для частноутвердительного суждения:
Некоторые S есть Р.
Некоторые Р не есть не-S.

4) для частноотрицательных суждений не используются выводы с применением противопоставления субъекту, так как в процессе этого вывода мы должны были бы сделать обращение частноотрицательного суждения, для которого не применяется вывод посредством обращения.

4. ОТНОШЕНИЯ МЕЖДУ СУЖДЕНИЯМИ

· by admin

· on 09.20.10

· ТЕМА 3. СУЖДЕНИЕ

· Комментарии отключены

·

Атрибутивные простые суждения по содержанию делятся на сравнимые и несравнимые. Несравнимые суждения – суждения, имеющие разные S или Р, или то и другое вместе: «Космос безграничен», «Драконовские законы жестоки».

Сравнимые суждения обладают одинаковыми S и Р, но могут различаться по качеству и количеству. Они делятся на совместимые и несовместимые. Совместимые суждения содержат одну и туже мысль – полностью или частично. Между ними возникают такие логические отношения: а) эквивалентности, б) подчинения, в) частичной совместимости.

а) Эквивалентность (равнозначность) – это отношение между суждениями, у которых S и Р выражены одними и теми же равнозначными понятиями, хотя и разными словами. «Все адвокаты – юристы» – «Все защитники в суде правоведы».

Последующие отношения между атрибутивными – A, E, I, O для наглядности изображаются в виде логического квадрата

Таблицы истинности

Вопрос об истинности простых суждений лежит вне сферы логики - на него отвечают конкретные науки, повседневная практика или наблюдение. Однако для установления истинности или ложности сложных суждений опыт не помощник.

Мы договариваемся, или принимаем соглашения относительно того, когда высказывания с той или иной логической связкой будем считать истинными, а когда — ложными. Соглашения, о которых идет речь, выражаются таблицами истинности для логических связок, показывающими, в каких случаях высказывание с той или иной связкой истинно, а в каких - мы будем считать его ложным. При этом мы опираемся на истинность или ложность простых суждений, являющихся компонентами сложного суждения. «Истина» («и») и «ложь» («л») называются «истинностными значениями» суждения - если переменная представляет истинное суждение, она принимает значение «истина»; если же она представляет ложное суждение, она принимает значение «ложь». Каждая переменная может представлять как истину, так и ложь.

Отрицаний применяется к одному суждению. Это суждение может быть истинным или ложным.

a	Ø а
и	л
л	и

Если исходное суждение истинно, то его отрицание мы договариваемся считать ложным; если же исходное суждение ложно, то его отрицание мы договариваемся считать истинным.

Таблицы истинности для остальных логических связок мы для удобства приводим все вместе:

	а	b	а Ù b	а Ú b	а Ú ^. b	а ® b	а «b
1.	и	и	и	и	Л	и	и
2.	и	л	л	и	и	л	л
3.	л	и	л	и	и	и	л
4.	л	л	л	л	л	и	и

Следует помнить, что союзы естественного языка гораздо богаче по своему смысловому содержанию, нежели логические связки. Последние схватывают лишь ту часть этого содержания, которая относится к соотношениям истинности и ложности простых высказываний. Более тонких смысловых связей между этими высказываниями логические связки не учитывают. Поэтому иногда возникает довольно большое расхождение между логическими связками и союзами естественного языка.

Наиболее отчетливо различие между логическими связками и союзами естественного языка выступает в случае импликации. Союз «если..., то...» обязательно предполагает смысловую, содержательную связь между простыми суждениями, которые он соединяет. Импликация же эту связь игнорирует, для нее безразлично содержание суждений a и b, соединенных знаком «®», важны лишь значения их истинности. Поэтому мы с полным правом можем утверждать, что импликация «Если Луна сделана из зеленого сыра, то Лондон находится во Франции» истинна, т. к. оба входящих в нее простых суждения ложны.

Дата добавления: 2014-11-25