Закон О. де Моргана

Преобразование сложных суждений.

1. Конъюнкция может быть выражена через дизъюнкцию: отрицание конъюнкции эквивалентно дизъюнкции отрицаний: ù (А L В) =

ù А V ù В. «Неверно, что Попцов следователь и в то же время судья» равнозначно суждению «Попцов не следователь или он не судья».

2. Дизъюнкция может быть выражена через конъюнкцию: отрицание дизъюнкции эквивалентно конъюнкции отрицаний: ù (А V В) =

ù А L ù В. «Неверно, что Смирнов изучал историю в вузе, или что он изучал ее самостоятельно» равнозначно суждению «Смирнов не изучал историю в вузе, и он не изучал ее самостоятельно».

Эти два вида преобразований сложных суждений носят название законов де Моргана.

3. Импликация может быть выражена через конъюнкцию: импликация эквивалентна отрицанию конъюнкции основания и ложного следствия: А→В = ù (А L ù В). «Если Петров милиционер, то он умеет стрелять». «Неверно, что Петров милиционер, и он не умеет стрелять».

4. Импликация может быть выражена через дизъюнкцию: импликация эквивалентна дизъюнкции ложного основания и следствия: А → В =

ù А V В.

«Если Смирнов судья, то он имеет специальное юридическое образование» «Или Смирнов не судья, или он имеет специальное юридическое образование».

Подытоживая сказанное надо отметить, что делая вывод в процессе преобразования суждения можно менять лишь логическую форму сложного суждения, его логический союз. Смысл же суждения должен оставаться тем же самым.

Установить же эквивалентность суждений можно при помощи таблиц истинности. Например, если мы сравним таблицы истинности конъюнкции и слабой дизъюнкции, то видно, что сложное суждение конъюнкции А L В истинно только тогда, когда истинны оба исходных суждения А и В; суждения дизъюнкции А V В ложны только в том случае, когда ложны и А, и В. Таким образом, логические союзы конъюнкции L и дизъюнкции V находятся, можно сказать, в обратной зависимости. Зная это, конъюнкцию можно выразить через дизъюнкцию, а дизъюнкцию через конъюнкцию. Получается именно эквивалентные формы, т.е. такие, которые истинны и ложны при одних и тех же значениях составляющих их суждений.

С помощью этого (благодаря замене одних суждений другими, эквивалентными им) можно упрощать сложные рассуждения, используя одни логические союзы вместо других.

Законы де Мо́ргана (правила де Мо́ргана) — логические правила, связывающие пары дуальных логических операций при помощи логического отрицания. Открыты шотландским математиком Огастесом де Морганом

Определение [править]

Огастес де Морган первоначально заметил, что в классической пропозициональной логике справедливы следующие соотношения:

not (P and Q) = (not P) or (not Q)

not (P or Q) = (not P) and (not Q)

Обычная запись этих законов в формальной логике:

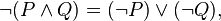
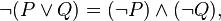
или

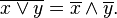
В исчислении предикатов:

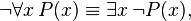
В теории множеств:

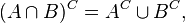
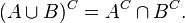
В виде теоремы:

Если существует операция логического умножения двух и более элементов, операция «и» — (A&B), то для того, чтобы найти обратное от всего суждения ~(A&B), необходимо найти обратное от каждого элемента и объединить их операцией логического сложения, операцией «или» — (~A + ~B). Закон работает аналогично в обратном направлении: ~(A+B) = (~A & ~B)

Дата добавления: 2014-11-25