Масса и импульс материальной точки

Второй закон Ньютона можно записать в иной форме, которая приведена самим Ньютоном в его главном труде «Математические начала натуральной философии». Если на тело (материальную точку) действует постоянная сила, то постоянным является и ускорени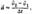е где — начальное и конечное значения скорости тела. Подставив это значение ускорения во второй закон Ньютона, получим: 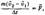или (1)

В этом уравнении появляется новая физическая величина — импульс материальной точки. Импульсом материальной точки называют величину равную произведению массы точки на ее скорость.

Обозначим импульс (его также называют иногда количеством движения) буквой . Тогда (1). Из формулы (1) видно, что импульс — векторная величина. Так как m > 0, то импульс имеет то же направление, что и скорость.

Единица импульса не имеет особого названия. Ее наименование получается из определения этой величины:

Чтобы определить массу некоторого тела, нужно сравнить ее с массой тела, принятого за эталон массы. Можно также сравнить массу данного тела с массой некоторого тела с уже известной массой (определенной путем сравнения с эталоном). Операцию сравнения масс m1 и m2 двух материальных точек (частиц) можно осуществить следующим образом. Поставим эти частицы в такие условия, чтобы их взаимодействием с другими телами можно было пренебречь. Система тел, взаимодействующих только между собой и не взаимодействующих с другими телами, называется замкнутой. Следовательно, мы рассматриваем замкнутую систему двух частиц. Если заставить эти частицы взаимодействовать (например, посредством столкновения друг с другом), их скорости получат приращения Δv1 и Δv2. Опыт дает, что эти приращения всегда имеют противоположные направления, т. е. отличаются знаком. Отношение же модулей приращений скоростей независит от способа и интенсивности взаимодействия данных двух тел. Это отношение принимается равным обратному отношению масс рассматриваемых тел: (1) Более инертное тело, т. е. тело с большей массой, претерпевает меньшее изменение скорости. Приняв во внимание противоположное направление векторов изменения скорости, соотношение (1) можно написать в виде: (2). В классической механике масса тела считается постоянной величиной, не зависящей от скорости тела. При скоростях, малых по сравнению со скоростью света с=3.108 м/с, это предположение практически выполняется. Воспользовавшись постоянством массы, представим (2) как: (3). Произведение массы тела на его скорость называется импульсом тела (по-старому - количество движения). Обозначив импульс буквой р, получим: (4) Определение (4) справедливо для материальных точек и протяженных тел, движущихся поступательно. В случае протяженного тела, движущегося непоступательно, нужно представить тело как совокупность материальных точек с массами , определить импульсы этих точек и затем сложить эти импульсы векторно. В результате получится полный импульс тела: (5) При поступательном движении скорости всех точек тела одинаковы, и (5) переходит в (4). Заменив в (3) произведения массы на скорость импульсами, придем к соотношению , или . Если изменение какой-то величины равно 0, это означает, что величина остается постоянной. Т.о., мы пришли к выводу, что полный импульс замкнутой системы двух взаимодействующих частиц остается постоянным: (6) закон сохранения импульса. В релятивистской механике выражение для импульса имеет более сложный вид, чем (4): (7)В (7) под массой подразумевается так называемая масса покоя тела, с – скорость света. Т.е. (7) можно истолковать так, что масса тела в релятивистской механике не остается постоянной, как в классической, а меняется с ростом скорости, как 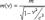(8)

Дата добавления: 2014-11-25