Плоско - параллельное движение твердого тела

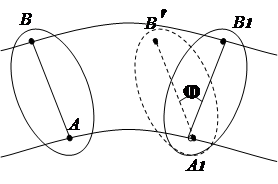
Плоскопараллельным называется движение твердого тела, при котором все его точки перемещаются в плоскостях, параллельных одной неподвижной плоскости (рис.2.10). Для изучения движения тела достаточно изучить движение одного сечения S этого тела плоскостью, параллельной неподвижной плоскости. Движение сечения S в своей плоскости можно рассматривать как сложное, состоящее из двух элементарных движений: а) поступательного и вращательного; б) вращательного относительно подвижного (мгновенного) центра.

В первом варианте движение сечения может быть задано уравнениями движения одной его точки (полюса) и вращением сечения вокруг полюса (рис.2.11). В качестве полюса может быть принята любая точка сечения.

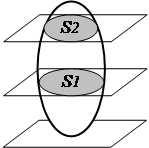Рис. 2.10 Рис. 2.11

Уравнения движения запишутся в виде:

Х _А = Х_А (t)

Y_А = Y_А (t) (2.14)

j_А = j_А (t)

Кинематические характеристики полюса определяют из уравнений его движения.

Скорость любой точки плоской фигуры, движущейся в своей плоскости слагается из скорости полюса (произвольно выбранной в сечении точки А) и скорости вращательного движения вокруг полюса (вращение точки В вокруг точки А).

Ускорение точки движущейся плоской фигуры складывается из ускорения полюса относительно неподвижной системы отсчета и ускорения за счет вращательного движения вокруг полюса.

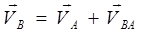
(2.15)

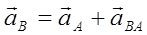(2.16)

Во втором варианте движение сечения рассматривается как вращательное вокруг подвижного (мгновенного) центра P (рис.1.12). В этом случае скорость любой точки В сечения будет определяться по формуле для вращательного движения

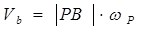_(2.17)

Угловая скорость вокруг мгновенного центра Р может быть определена если известна скорость какой либо точки сечения, например точки А.

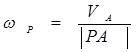(2.18)

Рис.2.12

Положение мгновенного центра вращения может быть определено на основании следующих свойств:

- вектор скорости точки перпендикулярен радиусу;

- модуль скорости точки пропорционален расстоянию от точки до центра вращения (V= w ∙R);

- скорость в центре вращения равна нулю.

Рассмотрим некоторые случаи определения положения мгновенного центра.

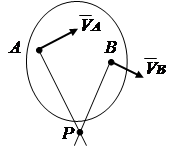
1. Известны направления скоростей двух точек плоской фигуры (рис.2.13). Проведем линии радиусов. Мгновенный центр вращения Р находится на пересечении перпендикуляров, проведенных к векторам скоростей.

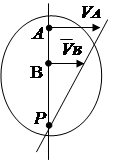
2. Скорости точек А и В известны, причем вектора и 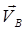параллельны друг другу, а линия АВ перпендикулярна (рис. 2. 14). В этом случае мгновенный центр вращения лежит на линии АВ. Для его нахождения проведем линию пропорциональности скоростей на основании зависимости V= wR.

3. Тело катится без скольжения по неподвижной поверхности другого тела (рис.2.15). Точка касания тел в данный момент имеет нулевую скорость в то время, как скорости других точек тела не равны нулю. Точка касания Р будет мгновенным центром вращения.

Рис. 2.13 Рис. 2.14 Рис. 2.15

Кроме рассмотренных вариантов скорость точки сечения может быть определена на основании теоремы о проекциях скоростей двух точек твердого тела.

Теорема: проекции скоростей двух точек твердого тела на прямую, проведенную через эти точки, равны между собой и одинаково направлены.

Доказательство: расстояние АВ изменяться не может, следовательно,

V _А cosa не может быть больше или меньше V _В cosb (рис.2.16).

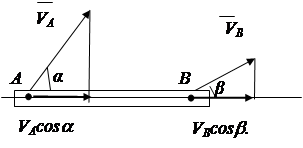Рис. 2.16

Вывод: V_А cosa = V_В cosb. (2.19)

Дата добавления: 2014-11-25