Основные понятия динамики

Задачи динамики

Динамика

Вопросы для самоконтроля по разделу

1. В чем состоят основные задачи кинематики? Назовите кинематические характеристики.

2. Назовите способы задания движения точки и определение кинематических характеристик.

3. Дайте определение поступательного, вращательного вокруг неподвижной оси, плоскопараллельного движения тела.

4. Как задается движение твердого тела при поступательном, вращательном вокруг неподвижной оси и плоскопараллельном движении тела и как определяется скорость и ускорение точки при этих движениях тела?

В динамике решаются два типа задач. Первая состоит в определении действующих сил при заданном законе движения материального объекта (точки или системы). Вторая задача обратная первой: определяется закон движения материального объекта при известных действующих на него силах.

Инерционность - свойство материальных тел сохранять состояние покоя или равномерного прямолинейного движения, пока внешние силы не изменят этого состояния.

Масса - количественная мера инерционности тела. Единица измерения массы - килограмм (кг).

Материальная точка - тело, обладающее массой, размерами которого при решении данной задачи пренебрегают.

Центр масс механической системы - геометрическая точка, координаты которой определяются формулами.

(3.1)

где m_k, x_k, y_k, z_k - масса и координаты k - той точки механической системы,

m - масса системы.

В однородном поле тяжести положение центра масс совпадает с положением центра тяжести.

Момент инерции материального тела относительно оси – количественная мера инертности при вращательном движении.

Момент инерции материальной точки относительно оси равен произведению массы точки на квадрат расстояния точки от оси.

J_Z = m×r² (3.2)

Момент инерции системы (тела) относительно оси равен арифметической сумме моментов инерции всех точек.

J_Z = åm_k×r_k² (3.3)

Сила инерции материальной точки - векторная величина, равная по модулю произведению массы точки на модуль ускорения и направленная противоположно вектору ускорения

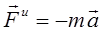(3.4)

Сила инерции материального тела - векторная величина, равная по модулю произведению массы тела на модуль ускорения центра масс тела и направленная противоположно вектору ускорения центра масс

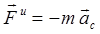, (3.5)

где 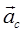- ускорение центра масс тела.

Элементарный импульс силы - векторная величина 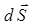, равная произведению вектора силы 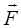на бесконечно малый промежуток времени dt

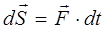, (3.6)

Полный импульс силы за Dt равен интегралу от элементарных импульсов

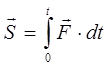(3.7)

Элементарная работа силы - скалярная величина dA, равная скалярному произведению вектора силы 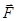на бесконечно малое перемещение d .

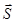Скалярное произведение векторов равно произведению их модулей на косинус угла между направлениями векторов.

dA = F×ds×cosa, (3.8)

где a - угол между направлениями векторов перемещения и силы.

Работа силы на конечном перемещении точки её приложения равна интегралу от элементарной работы, взятому по перемещению.

(3.9)

Единица измерения работы - Джоуль (1 Дж=1 Н×м).

Количество движения материальной точки - векторная величина 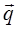, равная произведению массы m на её скорость .

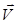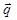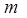
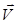= (3.10)

Количество движения механической системы 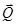равно векторной сумме количества движения её точек.

(3.11)

или с учетом формул (3.1).

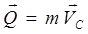, (3.12)

где: m- масса механической системы,

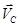- вектор скорости центра масс системы.

Кинетическая энергия материальной точки - скалярная величина Т, равная половине произведения массы точки на квадрат её скорости.

T= (3.13)

Кинетическая энергия механической системы равна сумме кинетических энергий всех её точек.

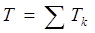(3.14)

Дата добавления: 2014-11-25