Найти наклонные и горизонтальные асимптоты графика функции

4. Использовать первую производную для определения области возрастания и убывания и экстремумов функции.

5. Использовать вторую производную для определения участков выпуклости и вогнутости графика и точек перегиба.

6. Построить график функции с учетом проведенного исследования.

Пример. Провести полное исследование функции

Решение:

Проведем полное исследование функции, используя следующую схему:

найти область определения функции;

исследовать на четность и нечетность функцию;

найти точки разрыва функции;

найти асимптоты (вертикальные, наклонные и горизонтальные) графика функции;

найти точки пересечения графика функции с координатными осями;

исследовать функцию на монотонность (указав интервалы возрастания и убывания) и экстремум;

определить интервалы выпуклости и вогнутости графика функции, точки перегиба;

при необходимости вычислить значения функции в дополнительных точках;

построить схематично график функции, используя результаты полученные в пунктах 1-8.

Областью определения функции является множество .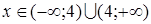

Так как и , то функция не является ни четной, ни нечетной.

Функция претерпевает разрыв в точке .

Найдем асимптоты графиков функции:

а). Прямая является вертикальной асимптотой, т.к.

,

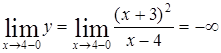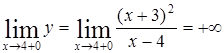
б). Находим наклонные и горизонтальные асимптоты (горизонтальные асимптоты являются частным случаем наклонных асимптот) ,

где ;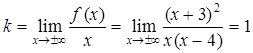

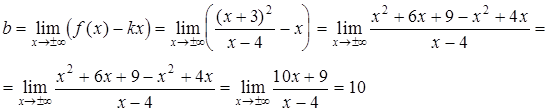
Таким образом, прямая 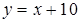является единственной наклонной асимптотой и на , и на .

Найдем точки пересечения графика функции с осями координат.

а) С осью 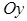: 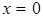, , 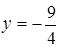т.е. точка пересечения с осью - .

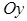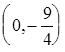б) С осью 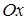: 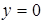, , 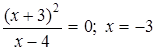т.е. точка пересечения с осью - .

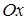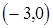6. Исследуем функцию на возрастание, убывание и экстремум. Для этого найдем производную функции.

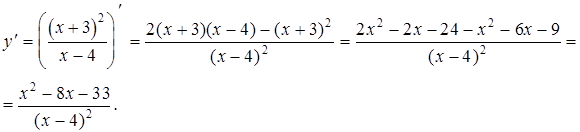
Из 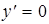получаем , откуда , .

+ _ +

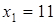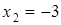______________________________________ x

-3 11

Так как на интервалах 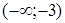и 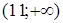производная положительна, т.е. 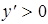, то график функции на указанных интервалах возрастает. Так как на интервале производная отрицательна, т.е. 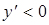, то на указанном интервале график функции убывает.

Так как при переходе через точки 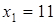, 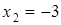производная функции меняет знаки и эти точки входят в область определения функции, то 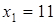, 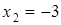- точки локального экстремума. Причем 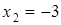точка локального минимума: 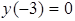(так как при переходе через нее производная меняет знак с "+" на "-"); 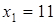- точка локального максимума: 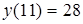(так как при переходе через нее производная меняет знак с "-" на "+").

7. Исследуем график функции на выпуклость, вогнутость и определим точки перегиба. Для этого найдем вторую производную функции.

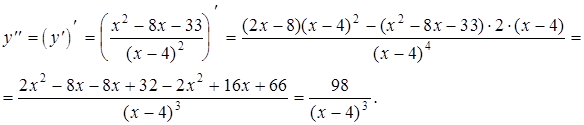
Очевидно, что в интервале 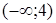вторая производная меньше нуля, т.е. 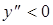, и в этом интервале график функции является выпуклым вверх. В интервале 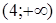вторая производная больше нуля, т.е. , и в этом интервале график функции является выпуклым вниз (вогнутым).

Несмотря на то, что при переходе через точку 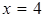вторая производная меняет знак, она не является точкой перегиба, так как 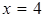не входит в область определения функции, т.е. функция в ней не определена. Таким образом, точек перегиба у графика функции нет.

Из 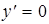получаем , откуда , .

+ _ +

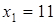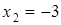______________________________________ x

-3 11

Так как на интервалах 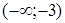и 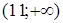производная положительна, т.е. 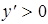, то график функции на указанных интервалах возрастает. Так как на интервале производная отрицательна, т.е. 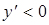, то на указанном интервале график функции убывает.

Так как при переходе через точки 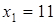, 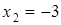производная функции меняет знаки и эти точки входят в область определения функции, то 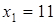, 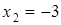- точки локального экстремума. Причем 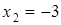точка локального минимума: 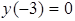(так как при переходе через нее производная меняет знак с "+" на "-"); 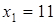- точка локального максимума: 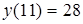(так как при переходе через нее производная меняет знак с "-" на "+").

4. Неопределенный интеграл

Часто возникает задача, обратная той, которая решалась в дифференциальном исчислении, а именно: дана функция 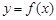, найти функцию , такую, что .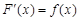

Функция называется первообразной для данной функции 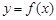на некотором промежутке Х, если для любого 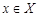выполняется равенство

.

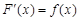Например, пусть 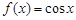, тогда за первообразную можно взять 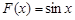, поскольку .

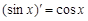В основе интегрального исчисления лежит теорема об общем виде первообразной: если – первообразная для функции 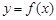на промежутке Х, то все первообразные для функции 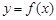имеют вид 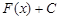, где С – произвольная постоянная.

Выражение вида 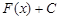описывает все первообразные для функции 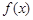. Действительно, для любой постоянной С

.

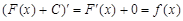Пусть наряду с данной первообразной функция 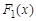– также первообразная для 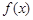. Тогда должны выполняться равенства

,

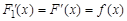откуда 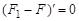. Следовательно, разность этих первообразных будет тождественно равна константе 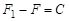или .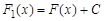

Действие нахождения первообразной называется интегрированием функции.

Доказанная теорема позволяет ввести основное понятие интегрального исчисления: если – первообразная для 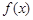, то совокупность функций 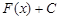, где С – произвольная постоянная, называется неопределенным интегралом от функции 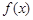, который обозначается следующим образом

.

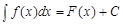Геометрически неопределенный интеграл представляет собой семейство плоских кривых 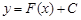, называемых интегральными.

Для того, чтобы проверить, правильно ли выполнено интегрирование, надо взять производную от результата и убедиться, что получена подынтегральная функция 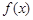. Как всякая обратная операция, интегрирование – более сложное действие, чем дифференцирование.

Приведем основные свойства неопределенного интеграла:

1. производная неопределенного интеграла равна подынтегральной функции

;

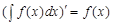2. неопределенный интеграл от алгебраической суммы функций равен сумме интегралов от слагаемых функций

;

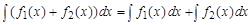3. постоянный множитель можно выносить за знак неопределенного интеграла

.

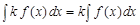Значения интегралов от основных элементарных функций получаются из формул дифференцирования этих функций. Приведем таблицу основных интегралов:

1) 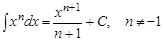;	7) ;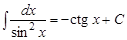
2) 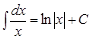;	8) ;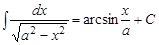
3) ;	9) ;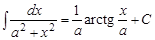
4) ;	10)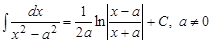
5) 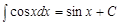;	11) ;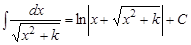
6) 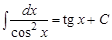;	12) .

Интегралы, содержащиеся в этой таблице, называются табличными.

Пример. Найти неопределенный интеграл. Результат интегрирования проверить дифференцированием

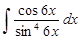
Решение: Для нахождения неопределенных интегралов можно воспользоваться как методом замены переменной, так и методом внесения под знак дифференциала. Покажем оба метода.

1. Воспользуемся методом замены переменной. Введем новую переменную t по формуле 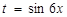. Тогда или 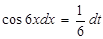. Тогда

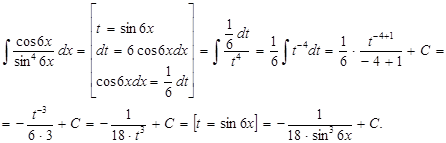
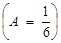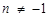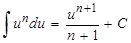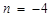После замены переменной воспользовались свойством неопределенного интеграла: постоянный множитель можно выносить за знак неопределенного интеграла, и так как , то пришли к табличному интегралу , где и .

2. Решим этот пример методом внесения под знак дифференциала. Замечая, что 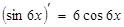и то, что подынтегральное выражение можно представить в виде

,

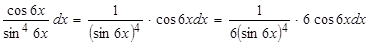внесем под знак дифференциала 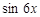. Для этого выпишем дифференциал этой функции . Тогда

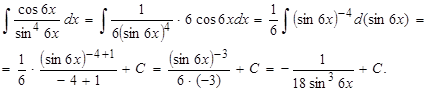
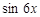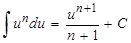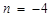После внесения под знак дифференциала функции пришли к табличному интегралу , где и .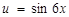

3. Результат интегрирования проверим дифференцированием. Для этого найдем производную

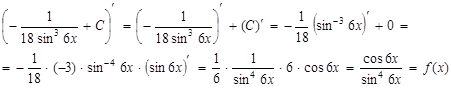
Таким образом, производная от неопределенного интеграла равна подынтегральной функции, следовательно, интеграл от данной функции найден, верно.

Дата добавления: 2014-11-25