
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Определенный интеграл
|
|
|
|
Определение определенного интеграла. Пусть функция 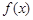 задана на отрезке [а, b]. Разобьем отрезок [а, b] на п произвольных частей точками
задана на отрезке [а, b]. Разобьем отрезок [а, b] на п произвольных частей точками
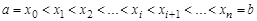 .
.
Точки, разделяющие отрезок [а, b] на частичные отрезки 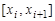 длиной
длиной 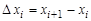 , называются точками разбиения. Внутри каждого частичного отрезка выберем произвольную точку
, называются точками разбиения. Внутри каждого частичного отрезка выберем произвольную точку 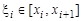 . Образуем сумму произведений
. Образуем сумму произведений
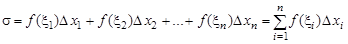 ,
,
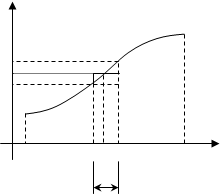
называемую интегральной суммой для функции 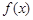 на отрезке [а, b]. Геометрический смысл величины s показан на рис. 2.. Это сумма площадей прямоугольников с основаниями
на отрезке [а, b]. Геометрический смысл величины s показан на рис. 2.. Это сумма площадей прямоугольников с основаниями 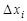 и высотами
и высотами 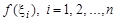 .
.
При этом числа a и b называются соответственно нижним и верхним пределами, выражение 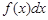 – подынтегральным выражением,
– подынтегральным выражением, 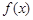 – подынтегральной функцией.
– подынтегральной функцией.
Определенный интеграл численно равен площади криволинейной трапеции, ограниченной вертикальными прямыми 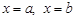 при
при 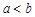 , осью Ох и графиком неотрицательной и непрерывной функции
, осью Ох и графиком неотрицательной и непрерывной функции 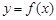 . В этом состоит его геометрический смысл.
. В этом состоит его геометрический смысл.
Если предположить, что 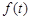 – производительность труда в момент t, то
– производительность труда в момент t, то 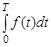 будет численно равен объему произведенной продукции за промежуток
будет численно равен объему произведенной продукции за промежуток 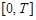 , т. е. определенному интегралу можно придать экономический смысл.
, т. е. определенному интегралу можно придать экономический смысл.
у
  В
Мi В
Мi
 mi
А
О х0=а хi
mi
А
О х0=а хi 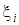 хi+1 b= хn х хi+1 b= хn х
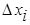 Рис. 2
Рис. 2
| Предел интегральной суммы 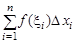 при стремлении при стремлении 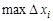 к нулю, не зависящий от способа выбора точек к нулю, не зависящий от способа выбора точек 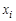 и точек и точек 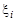 , называется определенным интегралом от функции , называется определенным интегралом от функции 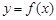 на [а, b] и обозначается на [а, b] и обозначается
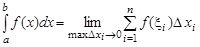
|
Определенный интеграл обладает рядом свойств, аналогичных свойствам неопределенного интеграла:
1) постоянный множитель можно выносить за знак интеграла;
2) интеграл от алгебраической суммы функций равен такой же сумме интегралов от этих функций (свойство линейности).
Кроме того, определенному интегралу присущи свойства, не имеющие аналогов в теории неопределенных интегралов:
3) интеграл от постоянной величины равен этой постоянной, умноженной на длину отрезка интегрирования
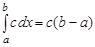 ;
;
4) при перемене местами пределов интегрирования интеграл изменяет лишь знак
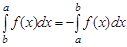 ;
;
5) интеграл с одинаковыми пределами интегрирования равен нулю
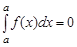 ;
;
6) для любых чисел а, b и c имеет место равенство
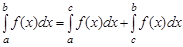 .
.
Пример. Вычислить определенный интеграл с точностью до двух знаков после запятой
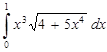
Решение:
Воспользуемся методом замены переменной. Введем новую переменную t по формуле 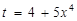 . Тогда
. Тогда 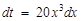 или
или 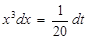 . Осуществим пересчет пределов интегрирования, используя вид замены. Подставим нижний предел интегрирования старой переменной
. Осуществим пересчет пределов интегрирования, используя вид замены. Подставим нижний предел интегрирования старой переменной 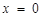 в выражение
в выражение 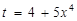 и найдем нижний предел интегрирования новой переменной
и найдем нижний предел интегрирования новой переменной 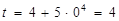 . Аналогично, подставляя верхний предел интегрирования старой переменной
. Аналогично, подставляя верхний предел интегрирования старой переменной 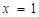 , найдем верхний предел интегрирования новой переменной
, найдем верхний предел интегрирования новой переменной 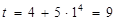 . Тогда
. Тогда
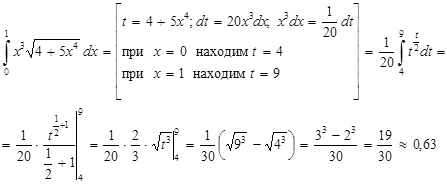
|
|
|
|
|
Дата добавления: 2014-11-25; Просмотров: 427; Нарушение авторских прав?; Мы поможем в написании вашей работы!