Окружность и перспектива

Многие из окружающих нас вещей имеют округлую форму: чашки, тарелки, очки, колёса… Список таких вещей широк, а потому изображение круга с учётом перспективы тоже требует определённого умения.

На рис. 4.1 изображён круг, вписанный в квадрат. Как вы можете видеть, этот круг действительно касается всех сторон квадрата, стороны которого являются касательными к окружности.

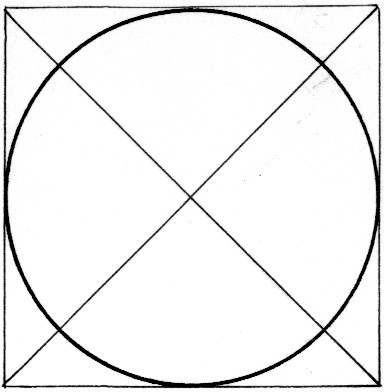
Рис. 4.1

Поскольку мы уже знаем, как изобразить квадрат (или прямоугольник) с учётом перспективы, то вписать в него круг (эллипс) будет несложно (рис. 4.2).

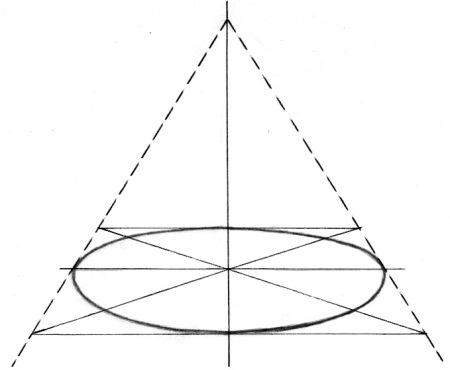
Рис. 4.2

На рис. 4.3 проведены примеры эллипсов. Это может быть и чуть сплюснутый круг, и фигура, уплощённая почти до прямой линии. Между этими двумя формами возможно огромное количество вариантов. Форма эллипса зависит, прежде всего, от формы прямоугольника, в который он вписан.

Рис. 4.3

Рисунок 4.4 должен служить нам напоминанием, что эллипс не имеет углов, а представляет собой сжатый круг. Закругление концов эллипса может быть сколь угодно острым, но по сути, это кривая линия – и она не должна сводиться к точке.

Рис. 4.4

На рис. 4.5 показано, что получается, когда вы рисуете вазу, имеющую форму цилиндра. Оба её края, и верхний и нижний, представляют из себя эллипсы (часть нижнего не видна), разные по форме. Тот эллипс, который находится дальше от линии горизонта, всегда будет более полным, чем тот, который находится ближе к линии горизонта.

Дата добавления: 2014-11-25