Решение. Основные требования к результатам исследования

Основные требования к результатам исследования

и построения графика:

1) все результаты исследования функции следует обосновать в ходе решения. Все исследования функции, включая все необходимые вычисления: вычисление пределов функции, вычисление производных в точках, решение уравнений, являются необходимой частью решения задачи на построение графика функции или кривой;

2) все результаты должны быть получены точно. Необходимые приближенные вычисления привести в решении задачи;

3) масштаб построения графика следует выбирать так, чтобы были отражены основные характерные моменты поведения графика функции;

4) на рисунке изобразить пунктирной прямой вертикальные, наклонные или горизонтальные асимптоты, указать уравнения асимптот;

5) обозначить точки минимума и максимума функции, указать их координаты;

6) обозначить точки перегиба графика функции, указать их координаты;

7) обозначить координаты точек пересечения кривой с координатными осями.

Пример. Построить график функции .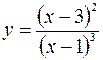

1. Областью определения данной функции является множество всех действительных чисел , кроме 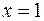, то есть .

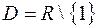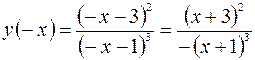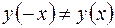2. Поскольку и и 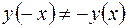, то функция не является четной и нечетной, то есть данная функция общего вида.

3. Находим асимптоты кривой.

Поскольку 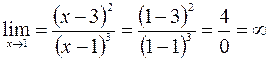, то 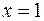– уравнение вертикальной асимптоты графика данной функции .

Наклонные асимптоты находим в виде уравнения прямой :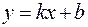

;

.

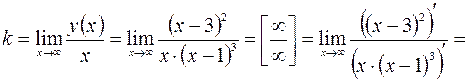
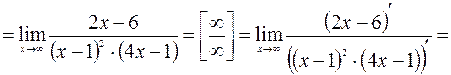
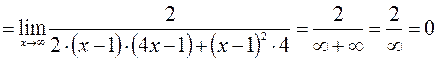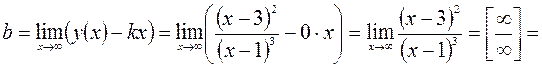
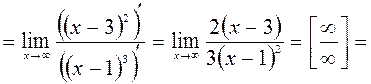
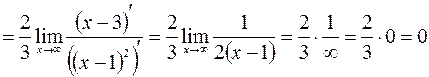Следовательно 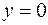– уравнение горизонтальной асимптоты графика данной функции .

4. Находим интервалы монотонности и точки экстремума функции.

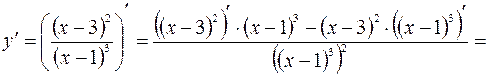
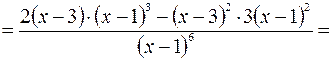
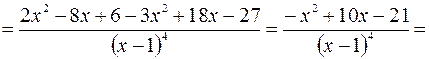
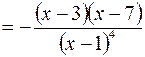
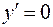
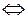
Используя необходимое условие экстремума, находим 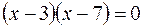, откуда 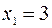или 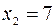; 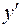не существует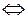 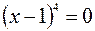, откуда .

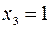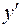Используем достаточные условия экстремума. Найденные три критические точки наносим на область определения и определяем знак в каждом из четырех интервалов.

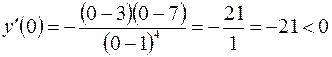
Так как 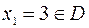и при переходе через эту точку 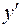меняет знак минус на плюс, то 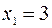– точка минимума функции , .

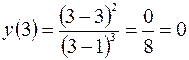Так как 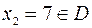и при переходе через эту точку 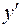меняет знак плюс на минус, то 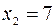– точка максимума функции , .

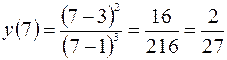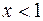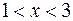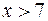
Так как при , , , 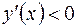то в интервалах 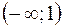, , 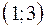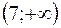функция монотонно убывает.

Так как при 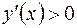, то в интервале 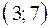функция монотонно возрастает.

5. Находим интервалы выпуклости (вогнутости) кривой и точки перегиба.

.

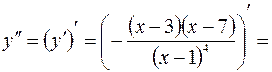
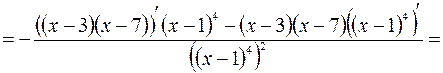
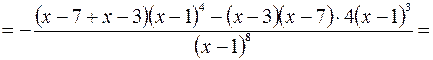
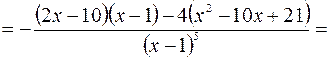
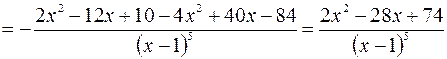Итак, .

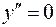
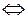
Используя необходимое условие перегиба, находим 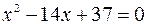, или 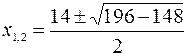, откуда 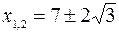; 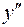не существует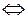 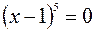, откуда .

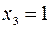Используем достаточные условия перегиба.

.

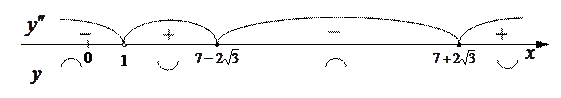
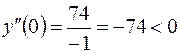Так как точки 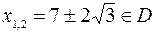и при переходе через эти точки 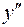меняет знак, то 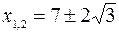– точки перегиба графика функции .

Так как при 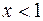, , 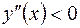то в интервалах 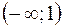, 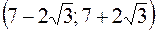функция выпукла вниз.

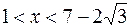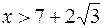
Так как при , , 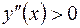то в интервалах 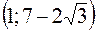, 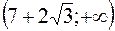функция выпукла вверх.

6. Находим координаты точек пересечения кривой с координатными осями:

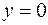
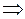
, откуда ;

.

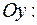
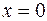
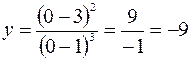7. Строим эскиз графика данной функции. (См. рис. 65).

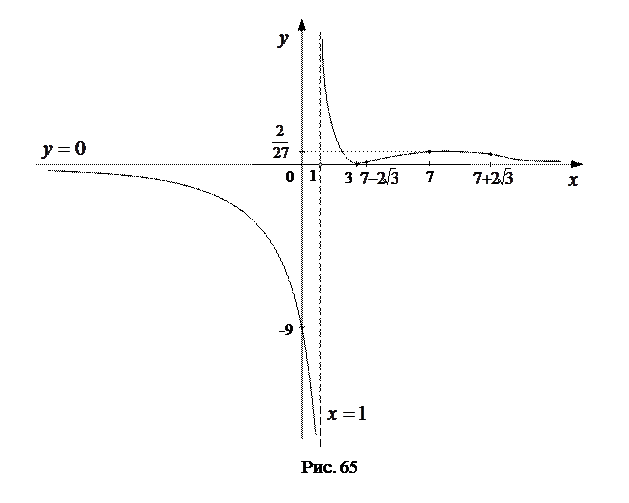
Контрольные задания

Задание 1

Найти матрицу 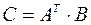, если:

1.01. , .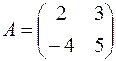

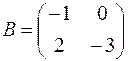1.02. , .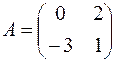

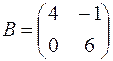1.03. , .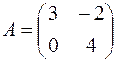

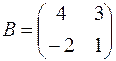1.04. , .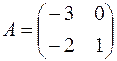

1.05. , .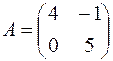

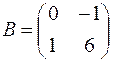1.06. , .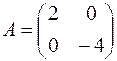

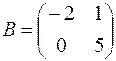1.07. , .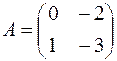

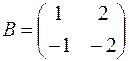1.08. , .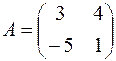

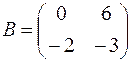1.09. , .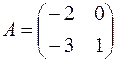

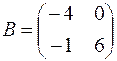1.10. , .

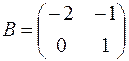Задание 2

Решить систему по правилу Крамера.

2.01. .

2.02. .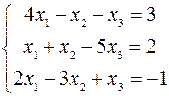

2.03. .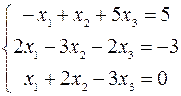

2.04. .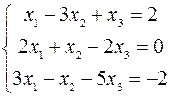

2.05. .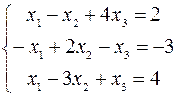

2.06. .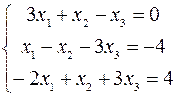

2.07. .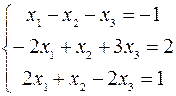

2.08. .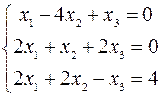

2.09. .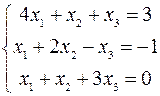

2.10. .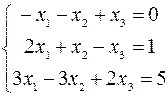

Задание 3

Дана пирамида 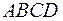. Найти:

1) угол 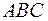грани ;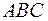

2) площадь грани ;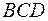

3) объем пирамиды 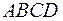, если

3.01. , , , .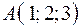

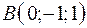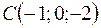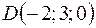3.02. , , , .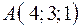

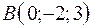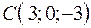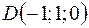3.03. , , , .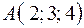

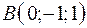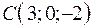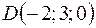3.04. , , , .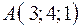

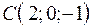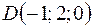3.05. , , , .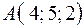

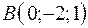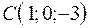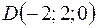3.06. , , , .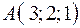

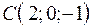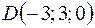3.07. , , , .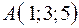

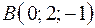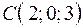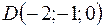3.08. , , , .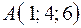

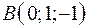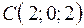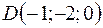3.09. , , , .

3.10. , , , .

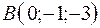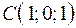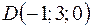Задание 4

Дан 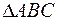. Найти:

1) уравнения его сторон;

2) уравнение высоты, опущенной из вершины 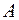на сторону ;

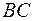3) уравнение медианы ;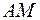

4)уравнение прямой, проходящей через точку 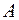и параллельной медиане 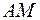, если

4.01. , , .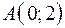

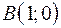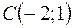4.02. , , .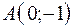

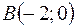4.03. , , .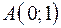

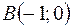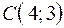4.04. , , .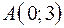

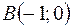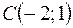4.05. , , .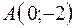

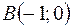4.06. , , .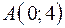

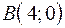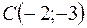4.07. , , .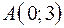

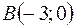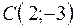4.08. , , .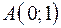

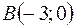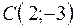4.09. , , .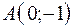

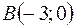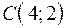4.10. , , .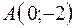

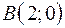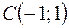Задание 5

Исследовать функцию и построить ее график:

5.1. .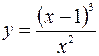

5.2. .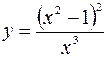

5.3. .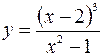

5.4. .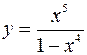

5.5. .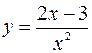

5.6. .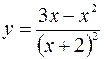

5.7. .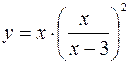

5.8. .

5.9. .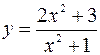

5.10. .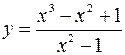

Литература

1. Важдаев В.П., Коган М.М., Лиогонький М.И., Протасова Л.А. 64 лекции по математике. Книга 1 (лекции 1-39): монография; Нижегор. гос. архитектур.-строит. ун-т – Н.Новгород: ННГАСУ, 2012.– 284 с.

2. Иванова С.В. Построение графиков функций и кривых. – М.: МФТИ, 2007. – 78 с.

3. Данко П.Е., Попов А.Г., Кожевникова Т.Е. Высшая математика в упражнениях и задачах. Часть 1.– М.: ООО Изд-во «Мир и образование», 2008 – 368 с.

Содержание

§1.	Линейная алгебра..............................................................................
	Матрицы и действия над ними.....……...……………………...........
	Определители......................................................................…….........
	Системы линейных уравнений...………………………………........
§2.	Векторная алгебра.............................................................................
	Линейные операции над векторами ………………………………..
	Действия над векторами в координатной форме..............................
	Скалярное произведение векторов.....................................................
	Некоторые приложения скалярного произведения..........................
	Векторное произведение векторов.....................................................
	Смешанное произведение векторов...................................................
§3.	Прямая на плоскости........................................................................
	Общее уравнение прямой....................................................................
	Взаимное расположение прямых на плоскости................................
§4.	Функция одного переменного.........................................................
	Основные понятия...............................................................................
	Основные элементарные функции.....................................................
	Предел числовой последовательности..............................................
	Предел функции...................................................................................
	Производная.........................................................................................
	Производная сложной функции.........................................................
	Производные высших порядков.........................................................
	Дифференциал функции......................................................................
	Правило Лопиталя................................................................................
	Исследование функций и построение их графиков..........................
	Симметрия функции............................................................................
	Асимптоты графика функции.............................................................
	Участки возрастания и убывания функции. Точки минимума и максимума............................................................................................
	Интервалы выпуклости и вогнутости кривой. Точки перегиба.......
	Основные требования к результатам исследования и построения графика..................................................................................................
	Контрольные задания.…………………………………………..........
	Литература.……………………………………………………...........

Павел Валерьевич Столбов  

Дата добавления: 2014-11-09