ЛЕКЦИЯ 5. Классификация моделей и параметров

Классификация моделей и параметров

Классификация моделей и параметров, используемых при автоматизированном проектировании

В автоматизированных проектных процедурах вместо еще не существующего проектируемого объекта оперируют некоторым квазиобъектом -моделью, которая отражает некоторые интересующие исследователя свойства объекта. Модели могут быть физическими (различного рода макеты, стенды) и математическими. Математическая модель – совокупность математических объектов (чисел, переменных, векторов, множеств и т. п.) и отношений между ними, которая адекватно отображает свойства проектируемого объекта, интересующие инженера-проектировщика. Эти модели называют математическими, если они формализованы средствами аппарата и языка математики.

Среди моделей различают функциональные, поведенческие, информационные, структурные модели (описания).

В свою очередь, математические модели могут быть геометрическими, топологическими, динамическими, логическими и т. п., если они отражают соответствующие свойства объектов. Наряду с математическими моделями при проектировании используют рассматриваемые ниже функциональные IDEFO-модели, информационные модели в виде диаграмм сущность - отношение, геометрические модели-чертежи.

Математические модели объекта могут быть функциональными, Д и они отображают физические или информационные процессы, Истекающие в моделируемом объекте, и структурными, если они отображают только структурные (в частном случае геометрические) свойства объектов. Функциональные модели объекта чаще всего представляют собой системы уравнений, а структурные модели объекта – это графы, матрицы и т. п.

Обычно при проектировании одного и того же объекта используется несколько моделей, различающихся сложностью и точностью.

Математическую модель объекта, полученную непосредственным отъединением математических моделей элементов в общую систему, называют полной математической моделью. Упрощение полной магматической модели объекта дает его макромодель. В САПР применение макромоделей приводит к сокращению затрат машинных времени и памяти, но за счет уменьшения точности и универсальности модели.

В дальнейшем, если нет специальной оговорки, под словом «модель» будем подразумевать математическую модель (МО).

Математическая функциональная модель в общем случае представляет собой алгоритм вычисления вектора выходных параметров Y при заданных векторах параметров элементов X и внешних параметров Q.

Математические модели могут быть символическими и численными. При использовании символических моделей оперируют не значениями величин, а их символическими обозначениями (идентификаторами). Численные модели могут быть аналитическими, т. е. их можно представить в виде явно выраженных зависимостей выходных параметров Y от параметров внутренних X и внешних Q, или алгоритмическими,, в которых связь Y, X и Q задана неявно в виде алгоритма моделирования. Важнейший частный случай алгоритмических моделей - имитационные, они отображают процессы в системе при наличии внешних воздействий на систему. Другими словами, имитационная модель -это алгоритмическая поведенческая модель.

Классификацию математических моделей выполняют также по ряду других признаков. Так, в зависимости от принадлежности к тому или иному иерархическому уровню выделяют модели уровней системного, функционально-логического, макроуровня (сосредоточенного) и микроуровня (распределенного).

По характеру используемого для описания математического аппарата различают модели лингвистические, теоретико-множественные, абстрактно-алгебраические, нечеткие, автоматные и т. п.

Например, на системном уровне преимущественно применяют модели систем массового обслуживания и сети Петри, на функционально-логическом уровне - автоматные модели на основе аппарата передаточных функций или конечных автоматов, на макроуровне - системы алгебраических и дифференциальных уравнений, на микроуровне - дифференциальные уравнения в частных производных. Особое место занимают геометрические модели, используемые в системах конструирования.

Кроме того, введены понятия полных моделей и макромоделей, моделей статических и динамических, детерминированных и стохастических, аналоговых и дискретных, символических и численных.

Полная модель объекта в отличие от макромодели описывает не только процессы на внешних выводах моделируемого объекта, но и внутренние для объекта процессы.

Статические модели описывают статические состояния, в них не присутствует время в качестве независимой переменной. Динамические модели отражают поведение системы, т. е. в них обязательно используется время.

Стохастические и детерминированные модели различают в зависимости от учета или неучета случайных факторов.

В аналоговых моделях фазовые переменные - непрерывные величины, в дискретных - дискретные, в частном случае дискретные модели являются логическими (булевыми), в них состояние системы и ее элементов описывается булевыми величинами. В ряде случаев полезно применение смешанных моделей, в которых одна часть подсистем характеризуется аналоговыми моделями, другая - логическими.

Информационные модели относятся к информационной страте автоматизированных систем, их используют прежде всего при мифологическом проектировании баз данных для описания связей между единицами информации.

Наибольшие трудности возникают при создании моделей слабоструктурированных систем, что характерно прежде всего для системного уровня проектирования. Здесь значительное внимание уделяется экспертным методам. В теории систем сформулированы общие рекомендации по подбору экспертов при разработке модели, организации экспертизы, по обработке полученных результатов. Достаточно общий подход к построению моделей сложных слабоструктурированных систем выражен в методиках IDEF.

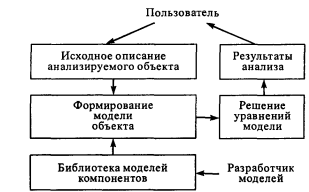
Рис. 3.1. Место процедур формирования моделей на маршрутах проектирования

Имитационное моделирование и его этапы

Термин имитационное моделирование используется во многих ситуациях, однако в сфере компьютерного моделирования он имеет вполне конкретный смысл, который, однако трудно определить одной фразой. Часть возможной двусмысленности проистекает из особенностей перевода текстов с английского на русский и наоборот, обусловленными некорректностью перевода слово-в-слово: далеко не все слова в разных языках имеют смысловые поля строго соответствующие друг другу.

В сфере компьютерного моделирования русскому термину имитационное моделирование соответствует английский термин simulation, в то время как более общему термину моделирование в английском соответствует modelling.

В настоящее время фактический смысл термина имитационное моделирование значительно расширился и с ним обычно связывают методологию изучения сложных систем на базе компьютерного моделирования. Более точно под этим подразумевается экспериментальное на базе модели) изучение макроповедения системы исходя из известного микроповедения ее элементов.

В отличие от общего математического моделирования (описания) объектов и явлений имитационное моделирование имеет смысл и дает наибольший эффект тогда, когда мы умеем решать прямую задачу, но не знаем, как достаточно просто и эффективно решать обратную за дачу. Именно такая ситуация весьма характерна для задач оптимального проектирования, многокритериальной оптимизации, принятия решений, прогнозирования и т.п.

Некоторые примеры:

1. Задана функция F(x), но в такой форме, что мы легко можем найти для конкретного x его образ x → F(x), но общего аналитического описания не имеем. Это бывает, если F(x) получается в виде результатов эксперимента, задана в виде таблицы или в виде алгоритма ее вычисления. Требуется найти корни (минимумы, максимумы).

1 Мы здесь говорим именно о терминах, то есть о словах с более или менее четко определенным смыслом в некоторой профессиональной сфере.

2. Известен алгоритм (правило) обслуживания очереди и вероятностные характеристики потока заявок на входе. Нужно найти вероятностные характеристики очереди (среднюю длину, среднее время обслуживания, вероятность потери заявок, переполнения...). Это - стандартная задача теории массового обслуживания.

3. Известны характеристики надежности элементов системы, структурная схема надежности. Нужно найти характеристики надежности всей системы.

4. Известны метрологические характеристики элементов измерительной системы и ее структурная схема. Нужно найти метрологические характеристики всей системы (прямая задача анализа погрешностей).

5. Известна модель измерительной системы с точки зрения прохождения сигнала со входа на выход. Найти сочетание управляемых параметров, обеспечивающих наилучшее значение заданного критерия эффективности (обратная задача).

Дата добавления: 2014-11-26