Типовые проектные процедуры

Создать проект объекта (изделия или процесса) означает выбрать структуру объекта, определить значения всех его параметров и представить результаты в установленной форме. Результаты (проектная документация) могут быть выражены в виде чертежей, схем, пояснительных записок, программ для программно-управляемого технологического оборудования и других документов на бумаге или на машинных носителях информации.

Разработка (или выбор) структуры объекта есть проектная процедура, называемая структурным синтезом, а расчет (или выбор) значений параметров элементов X - процедура параметрического синтеза.

Задача структурного синтеза формулируется в системотехнике как задача принятия решений (ЗПР). Ее суть заключается в определении цели, множества возможных решений и ограничивающих условий.

Классификацию ЗПР осуществляют по ряду признаков. По числу критериев различают задачи одно- и многокритериальные. По степени неопределенности различают ЗПР детерминированные, ЗПР в условиях риска (при наличии в формулировке задачи случайных параметров), ЗПР в условиях неопределенности, т. е. при неполноте или недостоверности исходной информации.

Реальные задачи проектирования, как правило, являются многокритериальными. Одна из основных проблем постановки многокритериальных задач - установление правил предпочтения вариантов. Способы сведения многокритериальных задач к однокритериальным и последующие пути решения изучаются в дисциплинах, посвященных методам оптимизации и математическому программированию.

Наличие случайных факторов усложняет решение ЗПР. Основные подходы к решению ЗПР в условиях риска заключаются или в решении «для наихудшего случая», или в учете в целевой функции математического ожидания и дисперсии выходных параметров. В первом случае задачу решают как детерминированную при завышенных требованиях к качеству решения, что является главным недостатком подхода. Во втором случае достоверность результатовnрешения намного выше, но возникают трудности с оценкой целевой функции.

Применение метода Монте-Карло в случае алгоритмических моделей становится единственной альтернативой, и, следовательно, для решения требуются значительные вычислительные ресурсы.

Существуют две группы ЗПР в условиях неопределенности. Одна из них решается при наличии противодействия разумного противника. Такие задачи изучаются в теории игр, для задач проектирования в технике они не характерны. Во второй группе противодействие достижению цели оказывают силы природы. Для их решения полезно использовать теорию и методы нечетких множеств.

Например, при синтезе структуры автоматизированной системы постановка задачи должна включать в качестве исходных данных следующие сведения:

• множество выполняемых системой функций (другими словами, множество работ, каждая из которых может состоять из одной или более операций); возможно, что в этом множестве имеется частичная упорядоченность работ, которая может быть представлена в виде ориентированного графа, где вершины соответствуют работам, а дуги - отношениям порядка;

• типы допустимых для использования серверов (машин), выполняющифункции системы;

• множество внешних источников и потребителей информации;

• во многих случаях задается также некоторая исходная структура системы в виде взаимосвязанной совокупности серверов определенных типов; эта структура может рассматриваться как обобщенная избыточная или как вариант первого приближения;

• различного рода ограничения, в частности ограничения на затраты материальных ресурсов и (или) на времена выполнения функций системы.

Задача заключается в синтезе (или коррекции) структуры, определении типов серверов (программно-аппаратных средств), распределении функций по серверам таким образом, чтобы достигался экстремум целевой функции при выполнении заданных ограничений.

Конструирование, разработка технологических процессов, оформление

проектной документации - частные случаи структурного синтеза.

Задачу параметрического синтеза называют параметрической оптимизацией (или оптимизацией), если ее решают как задачу математического программирования, т. е.

где F(X) - целевая функция; X - вектор управляемых (называемых также проектными или варьируемыми) параметров; D x = - допустимая область; ф(Х) и у(Х) - функции-ограничения.

Пример. Электронный усилитель: управляемые параметры X = (параметры резисторов, конденсаторов, транзисторов); выходные параметры Y = - верхняя и нижняя граничные частоты полосы пропускания; К- коэффициент усиления на средних частотах; - входное сопротивление). В качестве целевой функции F(X) можно выбрать параметр , а условия работоспособности остальных выходных параметров отнести к функциям-ограничениям.

Следующая после синтеза группа проектных процедур - процедуры анализа.

Цель анализа - получение информации о характере функционирования и значениях выходных параметров Y при заданных структуре объекта, сведениях о внешних параметрах Q и параметрах элементов X. Если заданы фиксированные значения параметров X и Q, то имеет место процедура одновариантного анализа, которая сводится к решению уравнений математической модели, например такой, как модель (1Л), и вычислению вектора выходных параметров Y. Если заданы статистические сведения о параметрах X и нужно получить оценки числовых характеристик распределений выходных параметров (например, оценки математических ожиданий и дисперсий), то это процедура статистического анализа. Если требуется рассчитать матрицы абсолютной А и (или) относительной В чувствительности, то имеет место задача анализа чувствительности.

Элемент матрицы А называют абсолютным коэффициентом чувствительности, он представляет собой частную производную у'-го выходного параметра по i- му параметру хi Другими словами, является элементом вектора градиентау'-го выходного параметра. На практике удобнее использовать безразмерные относительные коэффициенты чувствительности В, характеризующие степень влияния изменений параметров элементов на изменения выходных параметров:

где 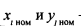— номинальные значения параметров 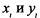соответственно.

В процедурах многовариантного анализа определяется влияние внешних параметров, разброса и нестабильности параметров элементов на выходные параметры. Процедуры статистического анализа и анализа чувствительности —характерные примеры процедур многовариантного анализа.

Этапы имитационного моделирования

Необходимо подчеркнуть, что само имитационное моделирование как познавательный процесс отнюдь не исчерпывается простым прогоном модели или экспериментированием с ней. Чтобы полностью оправдать свое предназначение прогон модели должен быть системно включен составной часть в более общий процесс.

Ниже приводятся основные этапы общего процесса имитационного моделирования согласно основополагающей книге Р. Шеннона [Шеннон Р.Ю. Имитационное моделирование систем - искусство и наука. М., Мир, 1978. - 418 с.].

1. Определение системы. (Постановка задачи - что нужно моделировать и с какой целью)

2. Формулирование модели (Переход от реальной системы к ее модели. Чаще всего через покомпонентное моделирование)

3. Проверка модели на адекватность.

а) в первом приближении (не дает ли абсурдных результатов);

б) проверка допущений;

в) проверка прохождения информации со входа на выход.

4. Стратегическое планирование. (Цель - уменьшение числа экспериментов за счет повышения их информативности).

5. Тактическое планирование.(Цель - оптимизация времени и точности отдельных экспериментов.)

а) за счет уменьшения времени переходных процессов;

б) за счет увеличения точности при сокращении объема выборки.

6. Экспериментирование. (Прогон модели)

7. Интерпретация. (Построение выводов по данным экспериментов,

формулирование ответа задачи, поставленной в п.1).

8. Реализация результатов моделирования. (Внедрение)

9. Документирование.

Формализация проектных задач и возможности применения САПР для их решения. Формализация проектной задачи является необходимым условием, для её решения в КС. К формализуемым задачам относятся прежде всего задачи, всегда считавшиеся рутинными, не требующими существенных затрат творческих усилий инженеров. Это, например, процедуры изготовления конструкторской документации (КД) в условиях, когда содержание КД уже полностью опреде­лено, но ещё не имеет принятой для хранения и дальнейшего ис­пользования формы (например, формы чертежей, графиков, схем алгоритмов, таблиц соединений); процедуры проведения электрических соединений в печатных платах или выполнения межпанельного и межстоечного монтажа. Кроме рутинных к формализуемым задачам относится большинство задач анализа проектируемых объектов. Их формализация достигается благодаря развитию теории и методов автоматизированного проектирования и прежде всего моделирования.

В настоящее время одним из направлений развития математического обеспечения автоматизированного проектирования является разработка методов и алгоритмов синтеза на различных уровнях иерархического проектирования КС.

Математический аппарат, используемый в САПР для разных уровней проектирования. Уровни проектирования включают в себя математическое описание структур и процессов, т. е. включают математические модели объектов. При этом для каждого-уровня характерно использование своего математического аппарата получения и анализа моделей. На компонентном уровне для описания электрических процессов в полупроводниковых компонентах электронных схем используются уравнения непрерывности, переноса и Пуассона, а для описания тепловых процессов – уравнения теплопроводности.

На схемотехническом уровне рассматриваются более сложные системы – совокупности компонентов, функционирующих в составе электронной схемы. Поэтому математическим аппаратом моделирования и анализа электрических процессов в электронных схемах является аппарат численного решения обыкновенных дифференциальных уравнений, в статических случаях вырождающихся в алгебраические и трансцендентные уравнения. На конструкторском этапе проектирования электронных схем используются уравнения такого же типа, с их помощью анализируются тепловые процессы в ПП, проверяются условия электромагнитной совместимости при коммутационно-монтажном проектировании.

На более высоких уровнях функционального проектирования в моделях отражаются процессы преобразования информации. Вместо фазовых переменных, описывающих электрические, магнитные или тепловые процессы, используются переменные, отражающие информационное состояние объектов. На функционально-логическом Уровне проектирования цифровой аппаратуры этими объектами являются логические вентили и блоки, их состояние характеризуется Дискретными, чаще всего булевыми, величинами. Поэтому используемый здесь математический аппарат – математическая логика (в том числе булева алгебра и теория конечных автоматов). На этом уровне в модели отображаются переменные и действия, которые выполняются моделируемым объектом в соответствии с алгоритмом функционирования. Здесь можно отождествлять информационные переменные с сигналами и поставить в соответствие каждому сигналу некоторую физическую величину – напряжение или ток на выходе конкретного элемента.

На системном уровне фигурируют объекты двух типов – устройства и заявки. И те, и другие имеют свои параметры, в том числе параметры, характеризующие их состояние.

Моделирование может использоваться для сокращения времени на каждом этапе процесса и для создания правильного проекта изделия - такого, который было бы легко воплотить в производство, легко продавать и обслуживать – в Самом начале процесса, до планирования основных затрат (оборудование и материалы).

О значении моделирования на этапе Концептуального Проектирования.

На этапе разработки концепции, основное решение на высшем уровне принимается исходя из рыночных потребностей в данном изделии, требований функциональности продукта и нужд бизнеса. Моделирование на этом этапе позволяет разработчикам концепции проверить ее, чтобы убедиться, что продукт можно изготовить в соответствии с заданными требованиями и потребительскими свойствами. Моделирование облегчает первоначальмую оценку различных концепций проекта, предоставляя возможность удовлетворения всех требований к функциональности в установленных рамках времени и затрат средств на выполнение работ по данному проекту.

О значении моделирования на этапе Детального Проектирования.

На этом этапе проект в целом уже определен, включая его отдельные узлы и компоненты с заданными потребительскими свойствами. Определены геометрия, материалы и стадии производственного процесса. Моделирование на этом этапе позволяет удостовериться, что данный проект реален, его можно будет выполнить и поставить на рельсы серийного производства. Весь проект может быть смоделирован, от системы в целом до каждого отдельного компонента. На этом этапе моделирование выполняется инженерами-разра­ботчиками и инженерами-технологами, планирующими производство.

О значении моделирования на этапе Испытаний. Это один из важных этапов в жизни проекта, т.к. он определяет дальнейшую судьбу изделия. Этап испытаний начинается тогда, когда доступен образец. Большинство компаний создают несколько натурных прототипов и подвергают их тщательному тестированию. Если экспериментальные образцы не проходят испытаний, проект изменяется и образец проходит новые испытания, до тех пор, пока не будет получен положительный результат. Такой цикл создания, испытания и устранения дефектов требует значительных временных, производственных и финансовых затрат. Моделирование может использоваться на этой стадии для уменьшения числа прототипов и физических циклов восстановления и повторного испытания, путем моделирование тестируемого образца на компьютере. Если тестируемый образец не проходит модельных испытаний, повторное изменение проекта очень недорого. Используя компьютерное моделирование на данном этапе удается сократить затраты на разработку прототи­пов более чем на 50%, а это значительная экономия времени и средств. Кроме этого, моделирование может быть использовано для сокращения времени и объема испытаний натурного образца. Например, при помощи моделирования можно «пробежаться» по образцу, сообщив «данные», которые бы измерялись при физическом испытании. Это позволяет инженерам, производящим испытание, заранее и более качественно определять критерии измерений и нагрузки/динамического нагру-жения, экономя время и исключая «работу вслепую» как часто бывает при лабораторных исследованиях.

О значении моделирования на этапе Производства.

Всем понятно, что на этом этапе продукция изготавливается. В данном случае моделирование используется для оптимизации процессов производства с целью минимизации отходов и этапов обработки. Моделирование улучшает процедуру изготовления продукта и снижает затраты на гарантийный ремонт, выявляя и исключая те параметры проекта, которые могут вызвать дефекты во время процесса производства. Более того, некоторые из новых производственных процессов, такие как гидроформование и суперпластическое формование, требуют моделирования для идентификации параметров производственного процесса, таких как температура,давление и скорость.

О значении моделирования на этапе Маркетинга/Продаж.

Моделирование может использоваться не голько для разработки и производства Вашей продукции. Оно также может применяться для маркетинга и продаж Вашей продукции. Мо­делирование можно использовать в коммерческих предложениях, чтобы показать, как Ваш продукт будет выглядеть в конкретных условиях и какими интересными свойствами он может быть интересен покупателю. Результаты моделирования могут использоваться в рекламе для придания Вашему продукту образа «высокотехнологичного». Ваши продажи увеличатся благодаря тому, что моделирование улучшает дизайн, а также саму продукцию, т.е. ее потребительские свойства.

О значении моделирования на этапе Поддержки и Сопровождения.

В дальнейшем, после реализации, Ваша продукция будет нуждаться в поддержке, техническом обслуживании, капитальном и текущем ремонте. Моделирование может использоваться на этом этапе для проведения ремонта и для модификаций изделия, обеспечивая корректировку проблемы, при этом одновременно сохраняя функциональность первоначального дизайна и набор полезных свойств. Задачи этого этапа очень четко просматриваются в аэрокосмической промышленности, где моделирование применяется для продления ресурса жизненного цикла изделий.

О значении моделирования на этапе Утилизации.

Это последний и тоже достаточно важный этап жизненного цикла изделий и технологий, особенно актуальный в настоящее время. Ничто не вечно в этом мире. Когда срок полезного использования изделия закончен, оно утилизируется или перерабатывается. Моделирование здесь применяется для выбора таких производственных процессов и упаковочных материалов, при которых возможна экономичная переработка изделия, включая различные типы материалов, которые были использованы для его изготовления. Во многих отраслях промышленности число «контактирующих частей» во время производства на порядок превышает число фактических частей в продукте. Применение моделирования позволяет спланировать их повторное использование или эффективную утилизацию еще на этапе эскизного проектирования самого изделия, значительно задолго до начала его эксплуатации.

1. ТРЕБОВАНИЯ К МАТЕМАТИЧЕСКОМУ ОБЕСПЕЧЕНИЮ

Свойства математического обеспечения (МО) оказывают существенное а иногда и определяющее влияние на возможности и показатели САПР.

При выборе и разработке моделей, методов и алгоритмов необходимо учитывать требования, предъявляемые к МО в САПР. Рассмотрим основные из них.

Универсальность. Под универсальностью МО понимается его применимость к широкому классу проектируемых объектов. Одно из отличий расчетных методов в САПР от ручных расчетных методов – высокая степень универсальности. Например, в подсистеме схемотехнического проектирования микропроцессорных устройств используются математические модели транзистора, справедливые для любой области работы (активной, насыщения, отсечки, инверсной активной, а методы получения и анализа моделей применимы к любой аналоговой или переключательной схеме на элементах из разрешенного списка; в подсистеме структурного проектирования этогоже устройства используются модели и алгоритмы, позволяющие исследовать стационарные и нестационарное процессы переработки информации при произвольных законах обслуживания в микропроцессоре и при произвольных входных потоках. В то же время каждая из ручных методик расчета справедлива при гораздо более серьезных ограничениях на типы объектов и режимы их работы.

Высокая степень универсальности МО нужна для того, чтобы САПР была применима к любым или большинству объектов, проектируемых на предприятии. Она делает удобным использование КС, прощая методику автоматизированного проектирования.

Степень универсальности не имеет количественной оценки. Реализуя ту или иную модель или метод, разработчик МО САПР должен указать четкие границы их применимости

Алгоритмическая надежность. К сожалению, не всегда условия применимости моделей и методов могут быть найдены, исследованы строгими методами и сформулированы в виде конкретных инструкций пользователям. Часто применимость того или иного компонента МО зависит от конкретных условий, многообразие которых не поддается счерпывающему учету и классификации. Методы и алгоритмы, не дающие строгого обоснования, называют эвристическими. Отсутствие четко сформулированных условий применимости приводит к тому, что эвристические методы могут использоваться некорректно. В результате либо вообще не будет получено решение (например, из-за отсутствия сходимости), либо оно будет далеким от истинного. Главная неприятность заключается в том, что в распоряжении инженера может не оказаться данных, позволяющих определить, корректны или нет полученные результаты. Следовательно, возможна ситуация, когда неверное решение будет использоваться в дальнейшем как правильное.

Предположим, что все заранее оговоренные ограничения на применение модели или метода соблюдаются. Свойство компонента МО давать при его применении в этих условиях правильные результаты называется алгоритмической надежностью. Степень универсальности характеризуется заранее оговоренными ограничениями, а алгоритмическая надежность – ограничениями, заранее не выявленными, следовательно, не оговоренными.

Количественной оценкой алгоритмической надежности служит вероятность получения правильных результатов при соблюдении оговоренных ограничений на применение метода. Если эта вероятность равна единице или близка к ней, то говорят, что метод алгоритмически надежен.

С проблемой алгоритмической надежности тесно связана проблема обусловленности математических моделей и задач. О плохой обусловленности говорят в случаях, когда малые погрешности исходных данных приводят к большим погрешностям результатов. На каждом этапе вычислений имеются свои промежуточные исходные данные и результаты, свои источники погрешностей. При плохой обусловленности погрешности могут резко возрасти, это может привести как к снижению точности, так и к росту затрат машинного времени. Для анализа и оптимизации объектов с плохо обусловленными моделями необходимо применять специальные методы с повышенной алгоритмической надежностью.

Точность. Для большинства компонентов МО важным свойством является точность, определяемая по степени совпадения расчетных и истинных результатов. Алгоритмически надежные методы могут давать различную точность. И лишь в случаях, когда точность оказывается хуже предельно допустимых значений или решение вообще невозможно получить, говорят не о точности, а об алгоритмической надежности.

В большинстве случаев решение проектных задач характеризуется;

совместным использованием многих компонентов МО, что затрудняет определение вклада в общую погрешность каждого из компонентов;

векторным характером результатов (например, при анализе находят вектор выходных параметров, при оптимизации – координаты экстремальной точки), т. е. результатом решения является значение не отдельного параметра, а многих параметров,

В связи с этим оценка точности производится с помощью специальных вычислительных экспериментов, в которых создаются условия для раздельной оценки погрешностей, вносимых математическими моделями элементов, алгоритмами анализа и оптимизации. В этих экспериментах используются специальные задачи, называемые тестовыми. Количественная оценка погрешности результата решения тестовой задачи есть одна из норм вектора относительных погрешностей – m-норма

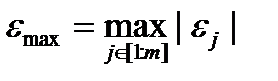или l — норма ,

где ej– относительная погрешность определения j-го элемента вектора результатов; т – размерность этого вектора.

Затраты машинного времени. Универсальные модели и методы характеризуются сравнительно большим объемом вычислений, растущим с увеличением размерности задач. Поэтому при решении большинства задач в САПР затраты машинного времени ТМ значительны.

Обычно именно ТМ являются главным ограничивающим фактором при попытках повысить сложность проектируемых на ЭВМ объектов и тщательность их исследования. Поэтому требование экономичности по ТМ – одно из основных требований к МО САПР.

При использовании в САПР многопроцессорных ВС уменьшить время счета можно с помощью параллельных вычислений. В связи с этим один из показателей экономичности МО – его приспособленность к распараллеливанию вычислительного процесса.

Требования высоких степени универсальности, алгоритмической надежности, точности, с одной стороны, и малых затрат машинного времени, с другой стороны, противоречивы. По этой причине любой конкретный компонент МО, отражая определенный компромисс в удовлетворении этих требований, может быть эффективным при решении одной задачи и малоэффективным при решении другой. Поэтому в САПР целесообразно иметь библиотеки с наборами моделей и методов, перекрывающими потребности всех пользователей САПР. Каждый компонент МО определенного целевого назначения должен быть представлен несколькими разновидностями, обеспечивающими разную степень компромиссного удовлетворения противоречивых требований.

Способы повышения экономичности МО, общие для различных подсистем САПР.

Значительное влияние на развитие МО САПР оказало стремление повысить экономичность используемых моделей и методов. Последнее достигается как разработкой экономичных моделей и алгоритмов, имеющих частный характер, так и совершенствованием и использованием общих принципов создания МО, эффективного по затратам машинных времени и памяти. К таким принципам относятся учет разреженности матриц, исследование сложных систем по частям (диакоптические методы исследования), макромоделирование, событийность анализа и рациональное использование эв­ристических способностей человека в интерактивных процедурах.

Учет разреженности матриц позволяет во многих алгоритмах, в которых используются операции над матрицами, добиться существенного сокращения затрат машинных времени и памяти. Этот учет основан на хранении в памяти ЭВМ только ненулевых элементов матриц и на выполнении арифметических действий только над ними.

Исследование сложных систем по частям реализуется в диакоптических методах исследования. Отличие диакоптического подхода проектирования от блочно-иерархического заключается в том, что диакоптика основана на использовании структурных особенностей анализируемых схем и выражающих их матриц, а не на принятии каких-либо упрощающих допущений. В диакоптических методах производится расчленение математических моделей на части, исследуемые самостоятельно.

Макромоделирование лежит в основе направления, связанного с рациональным выбором математических моделей элементов при построении математической модели системы. Макромоделирование реа­лизует возможность использования при анализе одного и того же объекта нескольких моделей, различающихся сложностью, точностью и полнотой отображения свойств объекта, трудоемкостью требующихся вычислений и т. п. Каждая из моделей соответствует определенному разбиению системы на элементы и выбору определенных моделей полученных элементов. Наиболее детальное разбиение в рамках данного иерархического уровня приводит к получению полной математической модели, характеризующейся высокой точностью, но и большим объемом требующихся вычислений. Очевидно, что повысить экономичность можно делением системы на более крупные блоки с использованием для блоков упрощенных математических моделей – макромоделей.

Событийность анализа заключается в том, что при имитации про­цессов, протекающих в исследуемом объекте, в каждый момент модельного времени вычисления проводятся только для небольшой части математической модели объекта. Эта часть включает в себя те элементы, состояние которых на очередном временном шаге может измениться. Использование принципа событийности существенно повышает экономичность анализа на функционально-логическом и системном уровнях проектирования.

Рациональное использование эвристических способностей человека (в интерактивных процедурах позволяет инженеру вмешиваться в ход вычислений и выбирать наиболее перспективные продолжения на основе эвристических оценок. Это выгодно во всех тех проектных процедурах, в которых следование только формальным критериям выбора дальнейших действий связано с чрезмерными затратами машинного времени.

Дата добавления: 2014-11-26