Функция выбора

Функция выбора в теории принятия решений имеет фундаментальное значение. Именно на ее построение в конечном итоге ориентировано решение задач формирования исходного множества альтернатив, анализа условий проведения операции, выявления и измерения предпочтений лица, принимающего решения.

Согласно формальному определению, принятому в ТПР, функция выбора — это формула вида (30):

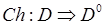, (30)

где D – некоторое (исходное) множество;

D° – подмножество (D° 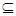D), обладающее известными или заданными свойствами.

Конкретный вид функции выбора, реализующий отображение (30), зависит от того, каков «механизм ситуации» (рисунок 2.9).

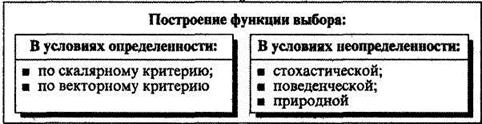
Рисунок 2.9 – Формы построения функции выбора

Функция выбора по скалярному критерию будет выглядеть следующим образом:

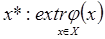, (31)

где extr φ(х) – экстремум заданной скалярной функции φ(х) векторного аргумента х.

Среди подобных проблемных ситуаций в практике управления часто встречаются следующие задачи принятия решений:

- составление оптимального плана транспортировки материальных средств;

- определение кратчайших маршрутов на заданной транспортной сети;

- принятие решений об оптимальной загрузке транспортных средств грузами;

- принятие решений о назначении исполнителей для выполнения работ какой-то целостной программы или проекта и др.

Как правило, все перечисленные задачи являются задачами дискретного математического программирования.

В задачах с векторным критерием нельзя с абсолютной уверенностью утверждать, что то или иное решение действительно оптимально. Один из вариантов решения может превосходить другой по одним критериям и уступать по другим (другому) критериям.

Трудности формализации функции выбора:

- описание элементов а множества А альтернатив, как функций некоторых их характеристик х, а границ множества – в виде системы равенств h(x)=0 и/или неравенств q(x)≤0, где фигурируют характеристики x;

- задание в явном формальном виде зависимостей значений результата y(a) или критерия W(a) от характеристик x,формально описывающих альтернативы;

- формальное описание вида функции полезности u(a) на альтернативах в виде некоторой функции φ(x) их характеристик х;

- интерпретация формального экстремума х* для предстваления ЛПР как наилучшей альтернативы а*.

Лекция 5 «Методы разработки управленческих решений»

Дата добавления: 2014-11-26