Стандартное отклонение доходности как мера риска

Как было показано, изменчивость показателей доходности акций зависит от и;

возможного диапазона и от вероятности появления экстремальных значений Для топ чтобы рассчитать и измерить изменчивость в распределении вероятностей получена возможных показателей доходности, в финансах чрезвычайно широко используете? стандартное отклонение (standard deviation) — статистический показатель, который вычисляется следующим образом.

Стандартное отклонение (σ) = Квадратный корень из суммы произведений вероятностей,

умноженной на возведенную в квадрат разность возможной доходности и ожидаемой (средней) доходности

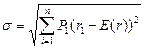
σ = Квадратный корень из [ P₁ (г₁ - Е (г))² + Р₂ (г₂ - Е (г))² +.... + Р_n (г_n - Е (г))²]

(10.2)

Чем больше стандартное отклонение, тем выше показатель изменчивости акции стандартное отклонение для безрисковых инвестиций, которые наверняка дадут 10% (Доходности, равняется нулю

σ= Квадратный корень из 1,0 х (10% -10%)² = 1,0 х (0,0) = О

Стандартное отклонение для акций Genco равно

σ = Квадратный корень из [(0,2)(30% -10%)² + (0,6)(10% -10%)² + (0,2)(-10% -10%)²]

σ = 12,65%

Стандартное отклонение для акций Risco равно

σ = Квадратный корень из [(0,2)(50%-10%)²+(0,6)(10%-10%)²+(0,2)(-30% - 10%)²!

σ =25,30%

Стандартное отклонение для акций Risco в два раза больше, чем для Genco, потому что возможное отклонение от среднего значения в два раза превышает тот же показательGenco.

В реальном мире диапазон показателей доходности акций не ограничен несколькими значениями, как в наших примерах, и доходность может принимать практически любое значение. Поэтому мы можем сказать, что распределение доходностей акций представляет собой непрерывное распределение вероятностей. Чаще всего используется один из видов непрерывного распределения вероятностей — нормальное распределение, которое представляет собой кривую, показанную на рис. 10.3.

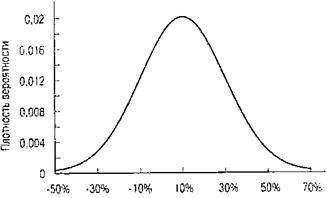
Доходность

Рис. 10.3. Нормальное распределение доходности акций Примечание. Средняя доходность составляет 10%, а стандартное отклонение равно 20%.

Для нормального и прочих, похожих на него, симметричных распределений стандартное отклонение — естественная единица измерения изменчивости. (Кстати, символ <т, которым обозначается стандартное отклонение, произносится как сигма.) Термины изменчивость и стандартное отклонение часто используются как взаимозаменяемые.

Нормальное распределение охватывает неограниченное количество значений доходности, от "минус бесконечность" до "плюс бесконечность". Для интерпретации различных значений стандартного отклонения обычно используется доверительный интервал (confidence interval) — статистический термин, которым обозначается определенный диапазон значений (это и есть "интервал"), в пределах которого фактическая доходность акции попадает с заданной вероятностью. Таким образом, при нормальном распределении доходность акции, которая находится в пределах доверительного интервала, включающего все значения доходности, находящиеся в рамках одного стандартного отклонения по обе стороны от среднего значения, имеет вероятность порядка 0,68. Соответствующий доверительный интервал для двух стандартных отклонений имеет вероятность порядка 0,95, а доверительный интервал для трех стандартных отклонений имеет вероятность порядка 0,99.

Рассмотрим, например, акции с ожидаемой доходностью в 10% и стандартным отклонением в 20%. При нормальном распределении существует вероятность, равная примерно 0,95, что фактическая доходность попадет в интервал, ограниченный с од_ ной стороны ожидаемой доходностью и двумя стандартными отклонениями (10% х 20% = 50%), а с другой стороны — ожидаемой доходностью минус два стандартных отклонения (10% - 2 х 20% = -30%). Диапазон доходностей, который ограничен ми_ нимальным значением -30% и максимальным значением 50%, с вероятностью О, представляет собой доверительный интервал для доходности данных акций.

Контрольный вопрос 10.

Каковы границы доверительного интервала для показателей доходности этих акций при условии, что вероятность их достижения составляет 0,99?

Дата добавления: 2014-11-09