Инвестирование и опционы 2 страница

Метод, используемый в данном случае, подобен тому, что применялся для получе­ния уравнения паритета опционов "пут" и "колл". При использовании только акций и безрискового займа конструируется синтетический опцион "колл". Далее в соответ­ствии с законом единой цены определяется цена опциона "колл", которая должна равняться цене построенного таким образом синтетического опциона "колл".

Рассмотрим одногодичный опцион "колл" с ценой исполнения 100 долл. Мы исхо­дим из того, что цена подлежащего пакета акций в данный м&мент составляет 100 долл. и может; вырасти «ли уиасть в течение года на 20%. Таким образом, на дату истечения опциона, через год, считая от сегодняшней даты,, цена может оказаться равной либо 120 долл., либо 80 долл. Безрисковая: процентная ставка равна 5% годовых.

Сравним теперь доход по опционам "колл" с доходом портфеля, состоящего из акций, покупка которых частично финансировалась с использованием средств, полу­ченных в кредит по безрисковой ставке. Поскольку в качестве обеспечения займа вы­ступают сами акции, максимальная сумма, которую инвестор может получить в виде займа под безрисковую процентную ставку, соответствует приведенной стоимости ак­ций, исходя из минимально возможной через год их цены. Минимальная цена равна 80 долл., таким образом сумма, которую можно получить взаймы сегодня, равна 80 долл. / 1,05 = 76,19 долл. Доходы по этому портфелю находятся в следующей зави­симости от курса акций через год.

' Далее следует найти, какая часть пакета акций необходима для дублирования дохо­да по опциону "колл". Такая часть называется коэффициентом хеджирования (Ьей^е гапо) опциона. В более широком смысле коэффициент хеджирования в двухступенча­той модели представляет собой разность между двумя возможными денежными пла­тежами по опциону, делённую на разность двух возможных предельных цен пакета подлежащих акций: В данном случае это

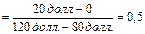
Таким образом, если бы мы купили 1/2 пакета акций и заняли для этих целей только 38,095 долл., у нас получился бы синтетический опцион "колл". Сумма займа представляет собой максимальную сумму, которая может быть совершенно опреде­ленно возвращена с процентами по наступлении срока истечения. Поскольку в нашем примере худший из возможных результатов для половины пакета акций составляет 40 долл., подлежащая займу.сумма равна приведенному значению 40 долл., дисконти­рованному по безрисковой процентной ставке 5%, что составляет 38,095 долл.

В табл. 15.6 показаны денежные платежи по самому опциону "колл" и посинтети-ческому опциону "колл", генерируемому таким дублирующим портфелем.

В соответствии с законом единой цены опцион "колл" и соответствующий ему дублирующий портфель (синтетический опцион "колл") должны иметь одинаковую стоимость, в результате чего цена опциона "колл" должна равняться

С =0,5^-38,095 долл. = 50 долл. - 38,095 долл. =11,905 долл.

15.6. ДИНАМИЧЕСКОЕ ДУБЛИРОВАНИЕ ОПЦИОНОВ И БИНОМИАЛЬНАЯ МОДЕЛЬ

Рабочая книга Достаточно очевидно, что предположение о существовании через год |Д| только двух возможных значений курса акций является совершенно нереальным. Для того чтобы сделать наш анализ более реалистичным, мы 15.6 дополнительно разделив годичный срок на два периода по полгода и предположим, что курс акций может вырасти либо снизиться в течение каждого полугодия на Ю долл. Таким образом, за год цена пакета акций может измениться максимально на 20 долл. в сторону повышения или понижения. Теперь в конце года будут существовать три возможных курса акций (120 долл., 100 долл. или 80 долл.), а соответствующие до­ходы по опциону "колл" составят 20 долл., О и 0.

Используемый метод состоит в нахождении стратегии инвестиционного самофинан­сирования (кЙГ-йпапсшй №уе51теп<: 51га1е8у), способной продублировать структуру де­нежных платежей (доходов) по опциону "колл" Эта стратегия оказывается динамиче­ской, требующей корректировки количества акций и объема займа по истечении шес­ти месяцев в соответствии со сложившимся к этому моменту курсом акций. Примем также, что после начального вложения денег инвестор не добавляет и не забирает средств.,! ''": ''!' ' ' • ' 1! •''"'' • •

В каждый момент времени данная стратегия сводится к тому, что уже было рас­смотрено в приведенной в предыдущем разделе двухступенчатой модели. На рис. 15.5 соответствующие операции показаны в виде дерева решений.

<

Начальный курс акций составляет 100 долл. (точка А). Вначале осуществляется по­купка 1/2 пакета акций за 50 долл., для чего берется заем в размере 45 долл. Таким образом, чистое вложение собственных денежных средств составляет 5 долл. В конце первого шестимесячного периода курс акций составляет либо 110 долл. (точка В), ли­бо 90 долл. (точка С). 13сли ситуация соответствует точке В, следует дополнительно получить заем в размере 55 долл. и купить вторую половину пакета акций. Если же реализуется ситуация, описываемая точкой С, то следует продать акции и погасить за­ем в 45 долл. Применение такой стратегии обеспечивает к концу года в точности те же денежные платежи, что и реализация опционного контракта.

Данная стратегия после первоначального вложения денежных средств основана на полном самофинансировании. Это означает, что до даты истечения опциона инвестор не вносит дополнительных средств и не забирает средств. Данный результат следует ив того, что, поскольку начальные затраты на применение самофинансирующейся ди­намической стратегии для формирования портфеля, дублирующего денежные платежи по опциону, составляют 5 долл., в соответствии с законом единой цены сумма в 5'долл. и должна выражать стоимость опциона.

(Рассмотренная выше модель оценки стоимости опциона более совершенна, чем двухступенчатая модель. Она называется биномиальной моделью оценки стоимости опциона11 (Ыпопиа! орйоп-рпств тоае1). Большая реалистичность и точность в биноми­альной модели достигаются при делении промежутка времени в один год на все меньшие и меньшие интервалы. Биномиальные модели оценки стоимости опционов широко применяются на практике. Число используемых промежутков времени зави­сит от требуемой в данном конкретном случае точности.

15.7. МОДЕЛЬ ЦЕНООБРАЗОВАНИЯ ОПЦИОНОВ БЛЭКА-ШОУЛЗА

Рабочая книга Более реалистичная и часто используемая на практике модель оценки стоимости опционов на акции — это модель Блэка—Шоулза". При ее выводе используются соображения, аналогичные 15.7 описанным выше, однако при этом предполагается осуществление не­прерывной корректировки дублирующего портфеля.

В исходную формулу Блэка—Щоулза для определения цены европейского опциона "колл", входят пять параметров, значение четырех из которых доступны инвесторам:

курс акций 5, цена исполнения Е, безрисковая процентная ставка (непрерывно на­числяемая процентная ставка в пересчете на год для безрисковых ценных бумаг со сроком погашения, равным сроку истечения опциона) г, и промежуток времени до срока истечения опциона Т.

Эта формула имеет вид:

(15.4)

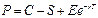
где 13

С — цена опциона "колл"

•У — курс акций

Е — цена исполнения опциона.

К -— безрисковая процентная ставка (непрерывно начисляемая процентная ставка

(в пересчете на год) для безрисковых ценных бумаг со сроком погашения, равным сроку истечения опциона))

Г—промежуток времени до срока истечения опциона в годах

а— риск подлежащей акции, измеряемый стандартным отклонением доходности акции, представленной как непрерывно начисляемый процент (в расчете на год)

1п—натуральный логарифм

е — основание натурального логарифма (приблизительно 2,71828)

М(а) — вероятность того, что значение нормально распределенной переменной меньше </

"По «опросам, связанным с развитием биномиальной модели, см. Сох, Лож$, ат1 КиЫпЛет, "Ор1юп Рпсту А ЗтрН^еЛ АрргоасН ", Лита! о/ Ппапсю! есопопчс!, 7 (1979), 229-263.

12 РксНег В1ас1с, ап(1 А/угоп ИсШез, "ТНе рпст^ о/ ОрИом апй ОЛег Согрога1е ЫаЫИИе5 ", Лита1 о/РоПНса! Есопоту, 81 (Мау/Лпе 1973).

13 Непрерывно начисляемая ставка доходности равна натуральному логарифму (1+ ставка до­ходности).

Выражение для стоимости опциона "пут" можно получить, произведя подстановку величины С из уравнения паритета опционов "пут" и "коля", т.е. воспользовавшись соотношением Р = С - 8 + Ее'^. В результате получаем формулу для нахождения стоимости опциона "пут":

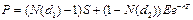
При выводе своего уравнения Блэк и Шоулзпредположили, чтоДо даты истечения опциона выплата дивидендов не производится. Мертон обобщил эту модель, добавив к ней возможность получения постоянного дивидендного дохода,' №14 В результат^ бы­ла получена формула для оценки стоимости опциона с учетом дивидендов:

(15.5)

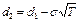
Обратите внимание на тот факт, что ожидаемая доходность акций в выражении для оценки стоимости опциона в явном виде не фигурирует. Ее влияние осуществля­ется через изменение курса акций. Любые изменения в ожиданиях Относительно бу­дущего курса акций или ожидаемой доходности от инвестиций в акции будут приво­дить к изменению курса акций и, таким образом, к изменению стоимости опциона "колл". Однако при любом заданном курсе акций цену опциона можно определить и не зная ожидаемой доходности акций. Финансовые аналитики, спорящие по поводу ожидаемой доходности акций, вполне могут, исходя из складывающегося курса акций, прийти к единому мнению относительно цены опциона.

В реальной ситуации ни изменчивость (о), ни дивидендная доходность акции (а) не известны с полной определенностью, и опыт свидетельствует о том, что обе эти величины подвержены случайным изменениям с течением времени. На практике ис­пользуются специально разработанные модели, учитывающие вероятностный характер этих переменных. Расчет с использованием формулы оценки стоимости опциона с корректировкой по выплате дивидендов, выраженной уравнением 15.5, легко прово­дится с применением электронных таблиц. Один из примеров таких расчетов включен в качестве приложения к этому учебнику.

Для удобства представим информацию в виде таблицы, подобно тому, как это сде­лано при расчете приведенной стоимости в главе 4; Предположим, например, что мы хотим рассчитать стоимость опционов "колл" и "пут" сроком на шесть месяцев с це­ной исполнения 100 долл., для которых курс подлежащих акций равен 100 долл., ди­видендная доходность составляет 3% годовых, а изменчивость курса акций равна 0,20. Безрисковая ставка равна 8% годовых. Исходные и выходные данные программы оценки стоимости опционов представлены в табл. 15.7.

Таблица 15.7. Таблица расчета стоимости опциона

S	E	R	T	d	s	Результаты
		0,08	0,5	0,03	0,2	С=6,79 долл.	Р=4,35 долл.

v " КоЬеП С. МеНоп, "ТНеогу о/КаНопа! ОрНоп Рпст^", Ве11Лита1 о/ Мапаутеп! 8с1епсе, 4 (Зрппе 1973).

В табл. 15.8 кратко охарактеризовано влияниешести исходных параметров на цены опционов "колл" и опционов "пут", всоответствии с уравнением 15.5.

Эта таблица интерпретируется следующим образом.

• Увеличение курса подлежащих акций приводит к росту цен на опционы "колл" и снижению цен на опционы "пут".

• Увеличение цены исполнения приводит к снижению цен на опционы "колл" и росту цен на опционы "пут".

• Усиление изменчивости курса акций приводит к росту цен как на опционы "колл", так и на опционы "пут".

• Увеличение промежутка времени до даты истечения опциона приводит к росту цен на опционы "колл" и росту цен на опционы "пут"15.

• Увеличение процентной ставки приводит к росту цен на опционы "колл" и снижению цен на опционы "пут".

• Увеличение дивидендной доходности приводит к снижению цен на опционы "колл" и росту цен на опционы "пут".

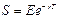В частном случае, когда курс акций, лежащих в основе опциона, равен приведен­ному значению цены "страйк" (т.е.

), для расчета цен опционов можно ис­пользовать удобную приближенную формулу

Такое приближение справедливо и для цены опционов "пут". Таким образом, если курс акций равен 100, цена "страйк" равна 108,33 долл., срок истечения составляет один год, безрисковая процентная ставка составляет 8%, выплаты по дивидендам рав­ны нулю, а изменчивость курса равняется 0,20, приблизительная стоимость как оп­циона "колл", так и опциона "пут" равна 0,08 цены акций, или 8 долл16.

Если для расчета соответствующих цен на такие опционы воспользоваться точной формулой (уравнение 15.5), окажется, что приближенная формула дает достаточно точные результаты:

15 Это относится только к американским опционам.

16 Обратите внимание на тот факт, что процентная ставка в приближенную формулу невходит.

15.8. ПОДРАЗУМЕВАЕМАЯ ИЗМЕНЧИВОСТЬ

Рабочая книга Подразумеваемая изменчивость (ппрИес! уо1а1Ш1у) определяется как такое

Ш значение о, при котором текущая рыночная цена опциона равна значе-1^ нию, рассчитанному с использованием формулы для оценки стоимости 15.8 опциона. Предположим, что В рассмотренном выше примере мы имеем значения, приведенные в левой части таблицы (включая цену 7,97 долл. для опциона "колл")

	Е	К	Г (Г	С	о
	108,33	0,08	1 0	7,97	?

Таблица 15.8. Факторы, определяющие цену опционов

Рост	Опцион «колл»	Опцион «пут»
Курс акций S Цены исполнения Е Изменчивости s Времени до даты истечения Т Процентной ставки r Денежных дивидендов d	Растет Снижается Растет Растет Растет Снижается	Снижается Растет Растет Растет Снижается Растет

Подставив эти величины в уравнение 15.6 и решив его относительно о; найдем изменчивость курса при такой цене опциона. В данном случае подразумеваемая из­менчивость курса акций равна 0,2.

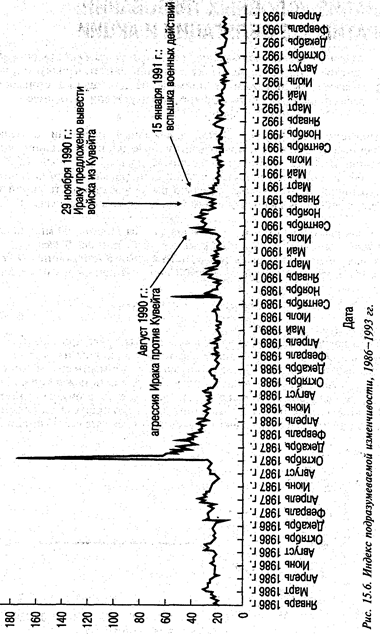
На чикагской бирже по торговле опционами СВОЕ строится индекс подразуме­ваемой изменчивости для индекса 5&Р 100, предназначенный для использования в качестве основы при заключении новых фьючерсных и опционных контрактов на базе подразумеваемой изменчивости17. Этот индекс подразумеваемой изменчивости (У1Х) предназначен для минимизации статистического отклонения при использовании ин­формации на основе значений восьми опционов на индексы 5&Р 100 со сроком исте­чения около 30 дней.

На рис. 15.6 показаны значения индекса подразумеваемой изменчивости У1Х за период с 1986 года по 1993 год. Видно, что в течение этого промежутка времени на­блюдались некоторые флуктуации этого индекса. Во время обвала на фондовом рынке в октябре 1987 года наблюдается высокий пик. В дальнейшем значение индекса вер­нулось к исходному значению.

77 Детальное описание построения индекса У1Х на бирже СВОЕ можно найти у К. Е. }УНа1еу, "ВетаНуез оп Маг1се1 Уо1аИИ(у: Неарп^ Гоой 1лп^ Оуегаие ", Лита1 о/ Ветайуе5 (Ра11 1993), рр. 80-82.

15.9. АНАЛИЗ УСЛОВНЫХ ТРЕБОВАНИЙ:

КОРПОРАТИВНЫЕ ОБЛИГАЦИИ И АКЦИИ

Рабочая книга M

Анализ условных требований (contingent claims analysis) опирается на рассмотренную ранее методику создания синтетического опциона. В этом разделе мы покажем ее применение для оценки стоимости долговых обязательств и капитала фирмы при условии, что имеется информация об общей стоимости фирмы.

Наша гипотетическая фирма Debtco, проводящая операции с недвижимостью, выпустила ценные бумаги двух типов: обыкновенные акции (1 миллион акций) и бескупонные облигации общей номинальной стоимостью в 80 млн долл. (80000 облигаций номиналом 1000 долл.). Срок погашения облигаций фирмы Debtco наступает через год, считая с сегодняшнего дня. Какова отдельно рыночная стоимость акций и облигаций фирмы Debtco, если общая рыночная стоимость этой фирмы составляет 100 млн долл.? Пусть V— текущая рыночная стоимость активов фирмы Debtco (100 миллионов долл.) Е — текущая рыночная стоимость акционерного капитала Debtco D — текущая рыночная стоимость заемного капитала (облигаций) Debtco Нам известно, что общая рыночная стоимость акционерного и заемного капитала этой фирмы равна 100 млн долл.:

V = D + Е = 100 млн долл.

Мы хотим получить отдельно значения Е и D.

Рассмотрим возможные доходы владельцев ценных бумаг при наступлении через год срока погашения облигаций. Доходные диаграммы приведены на рис. 15.7 и 15.8. Если стоимость активов фирмы превышает номинальную стоимость ее долговых обязательств (т.е. если f[ > 80 млн долл.), акционеры получают разность между этими двумя величинами (т.е. Fi—80 млн долл.). Однако в том случае, если стоимость активов окажется меньше 80 млн долл., компания не выполнит взятых долговых обязательств, а акционеры не получат ничего. Все активы фирмы достанутся держателям облигаций'⁸.

200 -

,s 160 -

I -t 120 -

»S

ё 80 - —————————————————

О 20 40 60 80 100 120 140 160 180 200 Стоимость фирмы через 1 год

Рис. 15.7. Доходная диаграмма для облигаций Debtco

Примечание. Если активы фирмы будут стоить меньше 80 млн долл., то держатели облигаций получат стоимость всех ее активов Если активы фирмы будут стоить больше 80 млн долл., то держатели облигаций получат только 80 млн долл.

" Такая ситуация наблюдается в том случае, если отсутствуют затраты на процедуру банкротства, а правила преимущественных выплат по обязательствам фирмы строго соблюдаются. В действительности же реализация процедуры банкротства требует определенных затрат.

Стоимость фирмы через год

Рис. 15.8 Доходная диаграмма для акций Debtco

Примечание Если активы фирмы будут стоить меньше 80 млн долл, то акционеры ничего не получат Если активы фирмы будут стоить больше 80 млн долл., то акционеры получат разность между стоимостью активов и 80 млн долл

Из рис. 15.7 видно, что, когда стоимость фирмы опускается ниже 80 млн долл., владельцы облигаций претендуют на все активы, а в случае, когда стоимость фирмы превышает 80 млн долл., владельцы облигаций получают только причитающиеся им 80 млн долл. Из рис. 15.8 следует, что если стоимость фирмы составляет меньше указанной суммы, то акционеры ничего не получают, а при стоимости фирмы, превышающей 80 млн долл., им достается разность между стоимостью фирмы и 80 млн долл.

Обратите внимание на тот факт, что доходная диаграмма для акционеров фирмы Debtco идентична доходной диаграмме для владельцев опционов "колл" если принять, что в основу опциона положены собственно активы фирмы, а цена исполнения равна номинальной стоимости долговых обязательств. Таким образом, мы можем применить для этого случая формулу 15 5, изменив соответствующим образом используемые в ней обозначения. Получаемая в результате формула, которую можно использовать для оценки стоимости акционерного капитала фирмы, имеет вид:

(15.6)

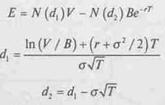
где

V— стоимость фирмы

Е— стоимость акционерного капитала фирмы

В — номинальная стоимость бескупонных дисконтных облигаций

г— безрисковая процентная ставка

f— промежуток времени до срока погашения облигаций в годах

а— стандартное отклонение непрерывно начисляемой ставки доходности активов

фирмы (в пересчете на год) In — натуральный логарифм

е — основание натурального логарифма (приблизительно 2,71828) N(d) — вероятность того, что значение нормально распределенной переменной

меньше d

Стоимость облигаций, D, по определению равна V — Е. Непрерывно начисляемая обещанная процентная ставка по долговым обязательствам R равна, таким образом,

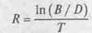
При применении уравнения 15 6 можно пользоваться теми же программами, что и для расчета стоимости опционов в соответствии с уравнением 15.5. При этом необходимо лишь иначе интерпретировать входные и выходные данные. Пусть безрисковая процентная ставка равна 8% годовых, а изменчивость стоимости активов фирмы составляет 0,3. В этом случае вместо табл. 15.7 мы получаем таблицу 15.7а.

Стоимость заемного капитала равна V — Е:

D = 100 млн долл. - 28,24 млн долл. = 71,76 млн долл.

Таким образом, обещанная непрерывно начисляемая процентная ставка по долговым обязательствам R равна

R = In (80 / 71,76) = 0,1087 или 10,87% годовых

В соответствии с полученными результатами и имея безрисковую процентную ставку в 8% годовых, потенциальным покупателям облигаций Debtco должна предлагаться доходность при погашении, равная 10,87%.

Таблица 15.7а. Расчет акционерного капитала [

ку. ' •'S'&Sgf' 1

V	в	ff	Г				Результат
		0,08				0,3	£ = 28,24 млн долл

Рассмотрим теперь частный случай, при котором стоимость активов фирмы равна приведенной номинальной стоимости облигаций, оцененной с применением безрисковой процентной ставки. Имеем выражение

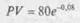
Приближенное значение для акционерного капитала корпорации в этом случае определяется как

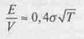
Пусть V= 100, В-= 108,33, о == 0,3, Г= 1; воспользовавшись приближением, приходим к

Е =12 млн долл. При использовании точной формулы получаем

	V	в	г	Г		Результат
		108,33	0,08		0,3	Е = 11,92 млн долл
Контрольный вопрос 15.8
Какой была бы доходность при погашении облигаций Debtco в рассмотренном выше частном случае?

Дата добавления: 2014-11-09