
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Вероятность ошибок при передаче сигнала по каналу с гауссовым шумом
|
|
|
|
Одним из важнейших критериев производительности цифровых систем связи является зависимость вероятности появления ошибочного бита Pb от отношения энергии сигнала, приходящейся на один бит, к спектральной плотности мощности аддитивного белого гауссовского шума Eb/N0. При этом предполагается, что единственным источником искажений сигнала является тепловой шум (АБГШ). Удобство использования отношения Eb/N0 вместо отношения мощности сигнала к мощности шума S/N, как в аналоговых системах связи, состоит в том, что так удобнее сравнивать производительность цифровых систем на битовом уровне. Это важно для цифровых систем, поскольку сигнал может иметь произвольное n-битовое значение (один символ может кодировать n бит). Предположим, что для данной вероятности возникновения ошибки в цифровом двоичном сигнале требуемое отношение S/N = 20. Поскольку двоичный сигнал имеет однобитовое значение, требуемое отношение S/N на бит равно 20. Пусть теперь сигнал является 1024-уровневым с теми же 20 единицами требуемого отношения S/N. Теперь, поскольку сигнал имеет 10-битовое значение, требуемое отношение S/N на один бит равно 2. Параметр Eb/N0 характеризует отношение сигнал-шум, приходящееся на один бит.
Параметр Eb/N0 связан с параметром S/N следующим соотношением:
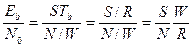
где Tb — время передачи бита, N — мощность шума, R — скорость передачи битов, W — ширина полосы. Отношение R/W называется спектральной эффективностью системы или эффективностью использования полосы частот и выражается в бит/с/Гц. Это отношение показывает, насколько эффективно система использует полосу частот.
Далее в таблице 1 приводятся выражения для вероятности битовой ошибки (для бинарных модуляций и модуляции QPSK) и вероятности символьной ошибки (для M-арных модуляций).
Графики вероятности битовой ошибки для различных бинарных систем показаны на рис. 4.
| Вид модуляции | Вероятность ошибки на бит Pb или на символPS | Примечание |
| BASK | 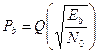 здесь и далее здесь и далее  - гауссов интеграл ошибок - гауссов интеграл ошибок
| Для ортогональных сигналов: S1(t)=Acoswt, S2(t)=0 0£t£T |
| BPSK | 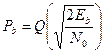
| Для антиподных сигналов: S1(t)=Acoswt, S2(t)= - Acoswt, 0£t£T |
| QPSK | 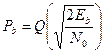
| |
| Ортогональная BPSK (когерентное обнаружение) | 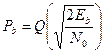
| |
| Ортогональная BPSK (некогерентное обнаружение) | 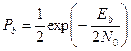
| |
| DPSK (некогерентное обнаружение) | 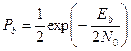
| |
| DPSK (когерентное обнаружение) | 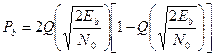
| |
| MPSK | 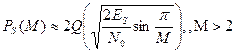
| Для больших отношений ES/N0, ES=Eblog2M – энергия, приходящаяся на символ, M=2K – количество равновероятных символов |
| DMPSK (некогерентное обнаружение) | 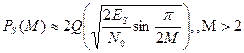
| См. примечание для MPSK |
| Ортогональная MFSK (когерентное обнаружение) | 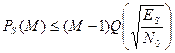
| ES=Eblog2M – энергия, приходящаяся на символ, M=2K – количество равновероятных символов |
| Ортогональная MFSK (некогерентное обнаружение) | 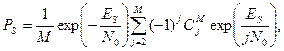
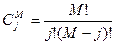
| См. примечание для MPSK с когерентным обнаружением |
| QAM | 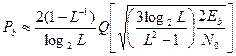
| Для прямоугольной решетки; L – количество уровней амплитуды в одном измерении; используется код Грея |
Можно показать, что соотношение между вероятностью битовой ошибки и вероятностью символьной ошибки для ортогональных M-арных сигналов даётся выражением:
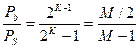
Аналогичное соотношение для многофазных сигналов MPSK при использовании кода Грея имеет вид:
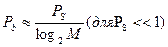
Код Грея — это код преобразования бинарных символов в M-арные, такие, что двоичные последовательности, соответствующие соседним символам (сдвигам фаз), отличаются только одним битом. На рис. 5 обычная бинарная кодировка сравнивается с кодировкой Грея. При появлении ошибки в M-арном символе наиболее вероятными являются ближайшие соседние символы, отличающиеся от переданного лишь одним битом, если используется кодировка Грея. Таким образом, высока вероятность того, что при кодировании с помощью кода Грея в случае возникновения ошибки ошибочным будет только один из k = log2 M переданных битов.
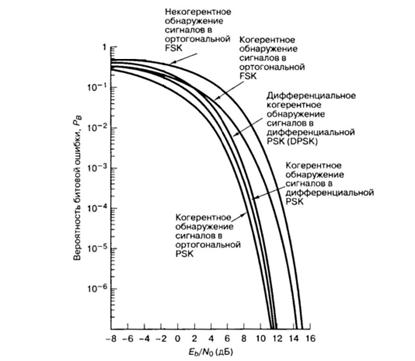
Рис. 4. Вероятность битовой ошибки для различных бинарных систем
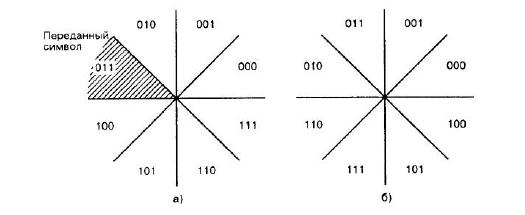
Рис. 5. Обычная кодировка (а) и кодировка Грея (б)
На рис. 6 приведены графики вероятности битовой ошибки для ортогональной M-арной (M = 2k) передачи сигналов с модуляцией MFSK с когерентным обнаружением, а на рис. 7 — графики вероятности битовой ошибки для многофазной (MPSK) передачи с когерентным обнаружением.
Как видно из сравнения этих рисунков, при ортогональной передаче с ростом k происходит уменьшение вероятности битовой ошибки, а при многофазной − увеличение.
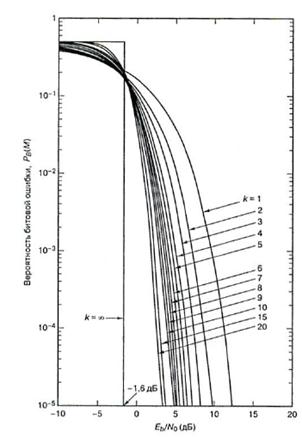
Рис. 6. Зависимость вероятности битовой ошибки от Eb/N0 для ортогональной M-арной передачи сигналов по каналу с гауссовым шумом с помощью модуляции MFSK при использовании когерентного обнаружения
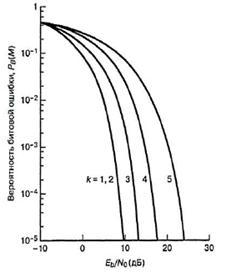
Рис. 7. Зависимость вероятности битовой ошибки от Eb/N0 для многофазной M-арной передачи сигналов по каналу с гауссовым шумом с помощью модуляции MPSK при использовании когерентного обнаружения
|
|
|
|
|
Дата добавления: 2014-11-08; Просмотров: 8096; Нарушение авторских прав?; Мы поможем в написании вашей работы!