Обработка полученных результатов

Контрольные вопросы

Содержание отчета

Задание

1. Создать структурную схему установки в среде LabView (рис. 1).

2. Для прямоугольного импульса и шумового сигнала сравнить вид сигналов и их спектры до и после прохождения через фильтр. Зарисовать все полученные осциллограммы (рис. 2).

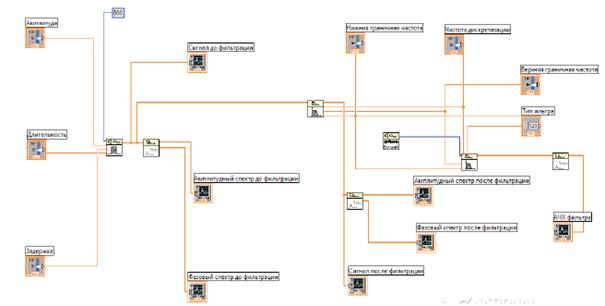
Рис 1. Структурная схема модели

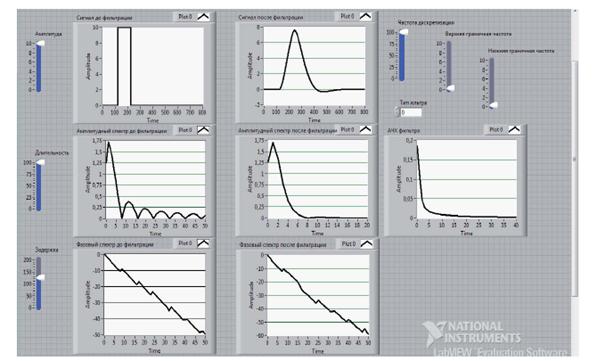
Рис. 2. Итоговая Front Panel. Прохождение сигнала через канал передачи (имитируется фильтрами различного вида)

3. Оценить амплитудно-частотные искажения, возникающие при прохождении сигнала через фильтр, имитирующий канал передачи. Для этого сравнить амплитудные спектры сигналов до и после фильтрации. В полосе частот, задаваемой преподавателем, оценить амплитудночастотные искажения при различных параметрах фильтра и сигнала.

4. Оценить возникающие фазочастотные искажения. Для этого сравнить фазовые спектры сигналов до и после фильтрации и построить фазочастотную характеристику фильтра, имитирующего канал передачи. На ее основе построить зависимость времени запаздывания спектральных составляющих сигнала на различных частотах. В полосе частот, задаваемой преподавателем, оценить неравномерность ГВЗ при различных параметрах фильтра и сигнала.

Проанализировать результаты.

Дополнительное задание (выполняется по указанию преподавателя)

1. Вместо фильтра поместить звено с нелинейной амплитудной характеристикой (односторонний или двусторонний ограничитель, квадратор, звено со степенной характеристикой разных степеней).

2. Выбрать генератор синусоидального сигнала.

3. Зарисовать сигналы до и после нелинейного звена.

4. Сравнить амплитудные спектры сигнала до и после нелинейного звена. Зарисовать спектрограммы.

5. В качестве источника сигнала создать сумматор синусоидальных сигналов от двух различных генераторов близких частот.

6. Повторить пп. 3 и 4.

7. Вместо генератора синусоидального сигнала использовать генератор шумового сигнала. Повторить пп. 3 – 5.

8. Проанализировать результаты.

1. Краткая теория.

2. Структурная схема.

3. Осциллограммы и спектрограммы.

4. Выводы.

1. Что такое искажения сигнала?

2. Из-за чего возникают фазочастотные искажения?

3. В чём проявляются амплитудно-частотные искажения?

4. В чём проявляются фазочастотные искажения?

5. Как и в чем измеряются амплитудно-частотные искажения?

6. Как и в чем измеряются фазочастотные искажения?

7. Какие еще виды искажений могут возникать при передаче сигналов?

8. Какие терминалы используются у генератора прямоугольных импульсов и на что они влияют?

9. Какие типы фильтров можно реализовать на базе фильтра Баттерворта?

10. На что влияет изменение нижней частоты среза?

11. В каких режимах работы фильтра используется верхняя частота среза?

12. Какие ограничения накладываются на верхнюю и нижнюю частоты среза?

13. Что такое коэффициент частотных, перекрестных и взаимномодуляционных искажений?

14. Как изменяются амплитудно-частотные искажения при изменении параметров фильтра?

15. Как изменяются фазочастотные искажения при изменении параметров фильтра?

Лабораторная работа №4

Эффективное кодирование сообщений. Коды Шеннона – Фано, Хаффмена

Цель работы: Изучение методов эффективного кодирования.

1. Краткие теоретические сведения

Задачи эффективного кодирования заключаются в следующем:

1. Запоминание максимального количества информации в ограниченной памяти.

2. Обеспечение максимальной пропускной способности источника сообщений.

Максимальное количество информации I, которое может передаться сигналом, определяется по формуле:

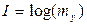(1)

где m_y - количество состояний сигнала.

Фактический объем переносимой информации определяется энтропией его множества сообщений Н. В связи с тем, что в основном в передаваемом наборе сообщений присутствуют типичные последовательности, сообщения передаются с относительной избыточностью D:

(2)

Для уменьшения избыточности символов необходимо применить эффективное кодирование. Эффективным называется способ кодирования, при котором:

Не возникает потери информации.

Требуется минимальное количество кодовых символов.

Для выполнения второго условия используются неравномерные коды, где длина кодового слова обратно пропорциональна вероятности его появления в сообщении.

Использование эффективного кодирования целесообразно, если вероятности появления различных букв существенно различаются, так как при этом энтропия множества букв (блоков) существенно меньше их информационной емкости.

Эффективное кодирование достигается благодаря учету априорных статистических характеристик источника информации.

Предельные возможности эффективного кодирования определяются:

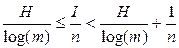(3)

При неравновероятности сообщений канал оказывается несогласованным с источником информации, в результате чего он не используется в полной мере.

Например, если на вход двоичного дискретного канала поступают преимущественно нули, то реле, выступающее в роли дискретного демодулятора, практически всегда находится в обесточенном состоянии, т.е. без дела. Наоборот, в случае передач одних единиц реле будет под током всегда, и его можно было бы не ставить, закоротив выход канала. Таким образом, если считать, что скорость передачи через дискретный канал есть среднее количество информации, проходящее через канал в единицу времени, то в рассмотренных случаях она мала. С другой стороны максимальная пропускная способность ДК определяется через полосу пропускания непрерывного канала Δf_k и может быть определена:

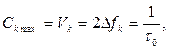бит,

где τ₀ - длительность одного символа.

Такая пропускная способность ДК будет реализована тогда, когда среднее количество информации, приходящееся на символ источника тоже максимально, например, если удельная энтропия двоичного источника равна 1 бит/символ.

Если энтропия источника меньше, канал недогружен даже в том случае, когда через него проходит 2Δfk символов в секунду. Производительность источника R будет меньше пропускной способности канала С.

Шеннон показал, что можно сообщения источника закодировать так, что среднее количество информации, приходящееся на символ источника, будет близко к максимальному. Это положение сформулировано в теореме Шеннона о кодировании для каналов без помех. Если производительность источника R меньше пропускной способности канала C_k, его сообщения можно закодировать так, что скорость передачи может быть как угодно близка к пропускной способности канала.

В соответствии с определением, 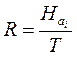, где - энтропия источника, T - средняя продолжительность кодовой комбинации: , здесь n_i- длина i-ой кодовой комбинации.

Отсюда,

Для выполнения равенства необходимо, чтобы , т.е. кодирование нужно осуществить так, чтобы длину кодовых комбинаций сообщений ставить в зависимость от количества информации, которое переносится данным сообщением или от вероятности данного сообщения. Часто встречающиеся, т.е. малоинформативные сообщения, следует кодировать короткими комбинациями, редко встречающиеся - длинными. В этом случае в среднем все сообщения источника будут закодированы меньшим числом символов, чем при любом другом способе кодирования. По этой причине данный код называется оптимальным или эффективным, а т.к. при его создании учитываются вероятности сообщений, он называется статистическим и без разделительных знаков, т.к. возможно однозначное декодирование, если при передаче нет ошибок за счет помех.

Алгоритм оптимального статистического кодирования предложили Фано и Хаффмен. Методика Фано заключается в следующем:

1. Подлежащие кодированию сообщения располагают в первом столбце в порядке убывания их вероятностей.

2. Сообщения разбиваются на две группы с примерно равными суммарными вероятностями. Группе, имеющей большую суммарную вероятность, приписывается наиболее вероятный символ кодовой комбинации, например - 0, второй группе - 1.

3. Сообщения, входящие в каждую из групп, вновь разбиваются на две группы с примерно равными вероятностями. И здесь, группе с большей вероятностью присваивается символ - 0, с меньшей - 1.

Этот процесс продолжается до тех пор, пока в каждой группе не останется по одному элементу.

Применение статистического кодирования имеет большое практическое значение. Например, при временном уплотнении линий связи в ночное время большинство абонентов не пользуется телефоном, и групповой сигнал в линии связи большей частью состоит из нулей. Производительность источника много меньше пропускной способности канала. Отключать абонентов нельзя, но их сообщения можно перекодировать статистическим кодом, они станут много короче, и в освободившееся время можно передавать другие сообщения, например, телеграммы, тексты газет и т.п.

Рассмотрим методику такого кодирования. Пусть статистика цифрового потока такова: вероятность нуля P(0)= 0,9, тогда P(1)=0,1.По таблице приложения 1 определяем энтропию источника. Н=0,469 бит/символ. Скорость передачи значительно меньше пропускной способности канала. Для согласования источника с каналом Шеннон предлагает укрупнять кодируемые последовательности.

Закодируем сообщения группами из двух символов. Получим четыре сообщения, которые вместе с их вероятностями представим таблицей:

Таблица 1

	0.81
	0.09
	0.09
	0.01

Найдем энтропию источника, пользуясь той же таблицей приложения.

Н=0,246+0,312+0,312+0,066=0,938 бит/сообщение. Средняя длина кодовой комбинации n = 0,81+0,09 *2+ 0,09 *3+ 0,01 *3 = 1,29 сим./сообщ. Удельная энтропия источника равна энтропии источника сообщений, деленной на среднюю длину комбинаций: Н/n=0,727 бит/сим. Эта энтропия существенно выше, чем была получена ранее (0,469), соответственно, стала выше и скорость передачи информации. При кодировании группами из трех сообщений удельная энтропия будет еще больше, а при дальнейшем укрупнении кодируемых последовательностей скорость передачи будет как угодно близка к пропускной способности канала, т.е. к 1/τ.Естественно, повышение скорости требует соответствующих затрат.

Кодирующее устройство в соответствии с таблицей 6.1 работает следующим образом. При поступлении на его вход комбинации 00 оно выдает в линию связи 0, при комбинации 01 – 11 и т.д. При кодировании группами из трех символов кодирующее устройство становится сложнее, оно должно формировать восемь групп выходных символов. При изменении входной статистики схемы кодирования продолжают кодирование, но с меньшей скоростью.

1.1 Основные понятия и приемы.

Под кодированием в широком смысле слова подразумевается представ­ление сообщений в форме, удобной для передачи по данному каналу. Опе­рация восстановления сообщения по принятому сигналу называется декоди­рованием. Одна из целей кодирования - путем устранения избыточности снизить среднее число символов, требующихся на букву сообщения, Пои отсутствии помех это непосредственно дает выигрыш во времени передачи или в объеме запоминающего устройства, т.е. повышает эффективность сис­темы. Поэтому такое кодирование получило название эффективного, или оптимального.

При построении оптимальных кодов наибольшее распространение полу­чили методики Шсннона - Фано и Хаффмена.

Согласно методике Шеннона - Фано построение оптимального кода ан­самбля из сообщений сводится к следующему:

1- й шаг. Множество из сообщений располагается в порядке убывания вероятностей.

2- й шаг. Первоначальный ансамбль кодируемых сигналов разбивается на две группы таким образом, чтобы суммарные вероятности сообщений обеих групп были по возможности равны.

3- й шаг. Первой группе присваивается символ 0, а второй группе - сим­вол 1.

4- й шаг. Каждую из образованных подгрупп делят на две части таким образом, чтобы суммарные вероятности вновь образованных подгрупп были по возможности равны.

5- й шаг. Первым группам каждой из подгрупп вновь присваивается 0, а вторым - 1. Таким образом, мы получаем вторые цифры кода. Затем каждая из четырех групп вновь делится на равные (с точки зрения суммарной веро­ятности) части до тех пор, пока в каждой из подгрупп не останется по одной букве.

Согласно методике Хаффмена, для построения оптимального кода N символы первичного алфавита выписываются в порядке убывания вероятностей. Последние n₀ символов, где 2£ n₀ £m и 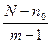- целое число, объединяют в некоторый новый символ с вероятностью, равной сумме веро­ятностей объединенных символов. Последние символы с учетом образован­ного символа вновь объединяют, получают новый, вспомогательный сим­вол, опять выписывают символы в порядке убывания вероятностей с учетом вспомогательного символа и так далее, до тех пор, пока сумма вероятно­стей m оставшихся символов не даст в сумме вероятность, равную 1. На практике обычно не производят многократного выписывания вероятностей символов с учетом вероятности вспомогательного символа, а обходятся эле­ментарными геометрическими построениями, суть которых сводится к то­му, что символы кодируемого алфавита попарно объединяют в новые сим­волы, начиная с символов, имеющих наименьшую вероятность. Затем с уче­том вновь образованных символов, которым присваивается значение сум­марной вероятности двух предыдущих, строят кодовое дерево, в вершине которого стоит символ 1.

Построенные по указанным выше методикам коды с неравномерным распределением символов, имеющие минимальную среднюю длину кодово­го слова, называют оптимальными неравномерными кодами (ОНК), или эффективными.

Рассмотрев методики построения эффективных кодов, нетрудно убе­диться в том, что эффект достигается благодаря присвоению более коротких кодовых комбинаций более вероятным буквам. Таким образом, эффект свя­зан с различием в числе символов кодовых комбинаций. А это приводит к трудностям при декодировании. Для этого эффективный код необходимо строить так, чтобы ни одна комбинация кода не совпадала с началом более длинной комбинации. Коды, удовлетворяющие этому условию, называются префиксными кодами. Нетрудно убедиться, что коды, получаемые в резуль­тате применения методики Шеннона-Фано или Хаффмена. являются пре­фиксными.

Эффективность оптимальных кодов оценивают при помощи коэффициента статистиче­ского сжатия:

К_сс=Н_мах/I_ср,

который характеризует уменьшение количества двоичных знаков на символ сообщения при применении ОНК по сравнению с применением ме­тодов нестатического кодирования и коэффициента относительной эффек­тивности К_оэ=Н/I_ср, который показывает, насколько используется статистическая избыточ­ность передаваемого сообщения.

Рисунок 1. Интерфейс приложения Eff_Code.

Построить оптимальный неравномерный код сообщения, для кото­рого далее вычисляются вероятности появления символов первичного алфавита. Опре­делить среднюю длину кода, коэффициенты относительной эффективности и статистического сжатия. Сравнить и обосновать различия в качественных характеристиках полученных кодов. Построение кода выполнить по мето­дике Шеннона-Фано и Хаффмена.

В результате выполнения лабораторной работы студенты должны про­демонстрировать умение построения оптимальных неравномерных кодов и оценку характеристик их эффективности. Должны быть представлены два ОНК, построенные для одних исходных данных различными методиками (Хаффмена и Шеннона-Фано), и вычислены их характеристики. Различия коэффициентов обосновать.

Дата добавления: 2014-11-08