Амплитудная модуляция с пассивной паузой

Оптимальный прием дискретных радиосигналов

Краткие теоретические сведения

Исследование устройств преобразования сигналов, использующих АМ, ЧМ и ОФМ модуляции

Лабораторная работа №5

Контрольные вопросы

1. Понятие об эффективном кодировании.

2. Энтропия источника сообщений.

3. Понятие о статистическом кодировании.

4. Коэффициента статистиче­ского сжатия.

5. Коэффициент относительной эффек­тивности

Цели работы:

1. Изучение методов амплитудной, частотной и относительной фазовой модуляции дискретных радиосигналов.

2. Оценка потенциальной помехоустойчивости приема амплитудно- (АМ) и частотно-манипулированных (ЧМ) и относительно-фазо-манипулированных (ОФМ) радиосигналов в аддитивной смеси их с тепловым шумом.

В настоящей лабораторной работе исследованию подлежат демодуляторы двоичных АМ – и ЧМ – радиосигналов, известных полностью. Это означает, что в точке приема сигналов, под которыми подразумеваются радиоимпульсы, соответствующие передаче двоичных «1» и «0» некоторой информационной последовательности, известны точно все их характеристики: длительности импульсов, частоты их заполнения и начальные фазы, временное положение импульсов и априорные вероятности появления этих импульсов. Неизвестным остается лишь сам факт появления одного из них на априорно известном интервале их появления.

В приемном устройстве на основании анализа реализации процесса y(t), представляющего собой аддитивную смесь напряжения сигнала и шумового напряжения на известном интервале возможного появления сигнала, определяется какой из возможных сигналов имеется в составе реализации y(t)=U_i(t)+U_ш(t), где U_i(t) сигнальный компонент реализации (i = 0 или 1 при передаче «0» и «1» соответственно), U_ш(t) – реализация теплового шума, представляющего собой непрерывный гауссовский процесс с равномерным энергетическим спектром в диапазоне частот, где сосредоточена основная часть спектра сигнальных компонентов U₁(t), U₂(t) («квазибелый шум»).

Эту задачу, решаемую в приемном устройстве, называют задачей распознавания или различения сигналов.

При использовании двоичной амплитудной модуляции (манипуляции) несущего гармонического колебания в системах связи передача элементарного сообщения – логической «1» осуществляется путем излучения радиоимпульса с длительностью t_{И .,} а передача элементарного сообщения – логического «0» осуществляется отсутствием излучения на таком же интервале t_{и .} Такой режим передачи называется режимом АМ с пассивной паузой. Во время этой пассивной паузы на входе приемника в составе реализации у(t) присутствует только шумовая составляющая U_ш(t), характеризуемая нормальной (гауссовской) плотностью вероятностей с нулевым средним значением и дисперсией σ²

и равномерной спектральной плотностью мощности

N (t) = N₀ =const

Из теории оптимальных методов радиоприема известно, что оптимальный приемник распознавания двоичных сигналов должен формировать на основе принятой реализации у(t) отношение правдоподобия

,

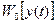где и - функции правдоподобия, вычисленные по реализации у (t) для случаев

y₁(t)=U₁(t)+U_ш(t) и y₂(t)=U₂(t)+U_ш(t).

При АМ с пассивной паузой U₂(t)=0 и y₂(t)= U_ш(t). Функции правдоподобия и 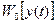являются условными функциями плотностей вероятностей реализации у(t), рассматриваемыми как функции условия (прием «1»или «0»)

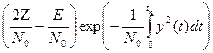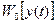= exp ,

= exp .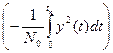

Таким образом, для двоичного АМ-сигнала с пассивной паузой

,

где Е = Е₁= Р_с1 t_и – энергия сигнала;

Р_с1 – мощность единичного элементарного радиоимпульса на входе приемника;

Z – корреляционный интеграл, определяемый выражением

,

где U₁(t) есть известная копия ожидаемого сигнала, соответствующая сообщению «1». Если в составе у(t) естьсигнал U₁(t), то

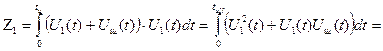
Если же в составе у(t) есть сигнал U₂(t)=0, то

.

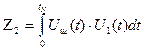Решение о приеме сигналов U₁(t) или U₂(t) принимается на основе сравнения

,

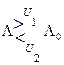где 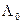- пороговое значение отношения правдоподобия.

Так как, 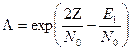является монотонной функцией корреляционного интеграла , являющегося единственной составляющей этого выражения, зависящей от принимаемой реализации у (t), то процедуру формирования 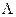в оптимальном приемнике можно заменить более простой процедурой вычисления корреляционного интеграла

.

Это следует из преобразований:

,

,

.

В том выражении правая часть неравенства представляет собой пороговое значение корреляционного интеграла

,

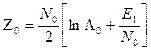по которому в конце интервала анализа (0… t_и) принимается решение о принятом сообщении «0» или «1».

В этом выражении в соответствии с моделью сигнала, известного полностью величина Е = Е₁ априорно известна. Известна также спектральная плотность мощности шума N₀, а пороговое значение Λ₀ определяется выбранным критерием различения, минимизирующим вероятность ошибочных решений.

Таким критерием является критерий Байеса, основанный на понятии функции среднего риска.

Значение корреляционных интегралов Z₁ и Z₂ являются случайными, так как Z₁ и Z₂ получены путем линейных операций над шумовой составляющей U_ш(t) реализации y(t), то можно утверждать, что значения Z₁ и Z₂ описываются нормальными плотностями вероятностей с соответствующими средними значениями Е₁ и ноль и одинаковыми дисперсиями (это следует из приведенных выше выражений Z₁ и Z₂).

При этом дисперсия

.

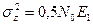На рисунке 3 схематично изображены две плотности вероятности W₁(Z) и W₂(Z), соответствующие корреляционным интегралам Z₁ и Z₂

Рисунок 3

На рисунке наглядно видно, что процедура принятия решения о различении сигналов на основе неравенства

сопровождается ошибочными решениями, характеризуемыми соответствующими вероятностями ошибок

и .

При этом увеличение порогового значения Z₀ увеличивает вероятность Р₁₀, но одновременно уменьшает Р₀₁. Оптимальный порог Z₀ должен минимизировать ущерб, наносимый ошибочными решениями. Этот ущерб описывается функцией среднего риска

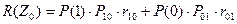
где Р(1) и Р(0) – априорные вероятности появления элементарных сообщений «0» и «1» в их длинной последовательности, r₁₀ и r₀₁ – количественное выражение ущерба, наносимого ошибочными решениями. В системах дискретной связи, как правило, средняя частота передачи «0» и «1» одинакова. Поэтому Р(1) = Р(0) = 0,5. Кроме этого считаются равными и значения r₀₁ = r₀₂, и принимаются они равными единице.

Тогда R(Z₀) = 0,5 (P₁₀+P₀₁). Эта величина должна минимизироваться выбором Z₀, то есть удовлетворить равенству

,

Это равенство при одинаковых дисперсиях распределений W₁(Z) и W₂(Z) соответствует оптимальному значению порога распознавания Z_{0 опт} = Е₁/2. а по отношению правдоподобия Λ_0опт=1, что соответствует частному случаю критерия распознавания Бейеса, называемому критерием «максимального правдоподобия».

Из вышеизложенного следует, что оптимальный приемник дискретных АМ – сигналов с пассивной паузой представляет собой последовательно включенные перемножитель, интегратор, и решающее устройство, которое совместно с формирователь логических уровней (ФЛУ) создает выходной видеосигнал. Функциональная схема такого приемника изображена на рисунке 4, а временные диаграммы процессов, происходящих в ее характерных точках – на рисунке 5.

Рисунок 4

Рисунок 5

Формирователь логических уровней (ФЛУ) на рисунке 5 может быть выполнен, например, на основе D – триггера, на вход которого поступает напряжение с выхода решающего устройства (РУ), а на тактовый вход подаются короткие импульсы от подсистемы тактовой синхронизации, появляющиеся незадолго до момента сброса интегратора, которое обеспечивается короткими импульсами сброса в конце каждого анализируемого интервала времени с длительностью t_и.

Вероятности ошибочных решений Р₁₀ и Р₀₁ при оптимальном значении порога распознавания Z₀ будут одинаковыми, зависящими от отношения сигнал/шум q на входе коррелятора, и могут быть вычислены по формуле

,

где - функция Крампа;

q= 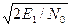– отношение сигнал/шум по напряжению на интервале передачи сигнала U₁(t).

Для сравнения помехоустойчивости дискретных сигналов с разными видами модуляции (АМ, ЧМ, ФМ) необходимо определить помехоустойчивость в зависимости от средней мощности принимаемого сигнала. В этом случае АМ – сигнал с пассивной паузой имеет среднюю мощность в два раза меньше мощности элемента сигнала U₁(t), то есть Р_ср = 0,5Р₁, и поэтому 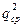= 0,5q².

Теперь вероятность ошибочного приема двоичного символа

.

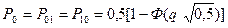Дата добавления: 2014-11-08