Разомкнутые символьные синхронизаторы

Символьная синхронизация

Для оптимальной демодуляции все цифровые приемники должны синхронизироваться с переходами поступающих цифровых символов. Ниже рассматривается несколько основных проектов символьных синхронизаторов. В центре обсуждения будет (для простоты записи и используемой терминологии) находиться случайный двоичный узкополосный сигнал, но расширение на недвоичные узкополосные сигналы должно быть очевидно.

При изложении материала в данном разделе предполагается, что о реальной информационной последовательности ничего не известно. Класс синхронизаторов, используемых в подобном случае, называется синхронизаторами без применения данных (non-data-aided — NDA). Существует еще один класс символьных синхронизаторов, которые используют известную информацию об информационном потоке. Эта информация может извлекаться из переданных по обратной связи решений относительно принятых данных или из введенной в информационный поток известной последовательности. В настоящее время более важными и доминирующими при выборе модуляций, эффективно использующих полосу, становятся методы с использование» данных (data-aided — DA). Эти методы рассматриваются в следующем разделе.

Рассматриваемые символьные синхронизаторы можно разделить на две основные группы. Первая группа состоит из разомкнутых синхронизаторов. Данные схемы выделяют копию выхода генератора тактовых импульсов передатчика непосредственно из поступающего информационного потока. Вторая группа — это замкнутые синхронизаторы; они синхронизируют локальный генератор тактовых импульсов с поступающим сигналом посредством сличения локального и поступающего сигналов. Замкнутые синхронизаторы, как правило, точнее, но при этом сложнее и дороже.

Разомкнутые символьные синхронизаторы также иногда называют нелинейными синхронизаторами на фильтрах [20]; данное название говорит само за себя. Синхронизаторы этого класса генерируют частотную компоненту со скоростью передачи символов, пропуская поступающий узкополосный сигнал через последовательность фильтра и нелинейного устройства. Работа данного устройства аналогична восстановлению несущей в контуре сопровождения с подавленной несущей. В данном случае желательный частотный компонент, передаваемый со скоростью передачи символов, изолируется с помощью полосового фильтра, после чего насыщающий усилитель с высоким коэффициентом насыщения придает ему нужную форму. В результате восстанавливается прямоугольный сигнал генератора тактовых импульсов.

На рис. 2 приведены три примера разомкнутых битовых синхронизаторов. В первом примере (рис.2, а) поступающий сигнал s(t) фильтруется с использованием согласованного фильтра. Выход этого фильтра — автокорреляционная функция исходного сигнала. Например, для передачи с помощью прямоугольных импульсов, на выходе имеем сигнал, состоящий из равнобедренных треугольников. Затем получен­ная последовательность спрямляется с помощью некоторой нелинейности четного по­рядка, например квадратичного устройства. Полученный сигнал будет содержать пики положительной амплитуды, которые с точностью до временной задержки, соответствуют переходам входных символов. Последовательность описанных процессов изображена на рис. 3. Таким образом, сигнал с выхода четного устройства будет содержать Фурье-компоненту на собственной частоте тактового генератора. Данная частотная составляющая изолируется от остальных гармоник с помощью полосового фильтра (bandpass filter — BPF), и ей придается форма посредством насыщающего усилителя с передаточной функцией следующего вида

Рис.2. Три типа разомкнутых битовых синхронизаторов

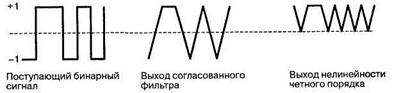
Рис.3. Иллюстрация процессов, проходящих в разомкнутом битовом синхронизаторе

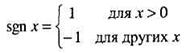(5)

Во втором примере (рис.2, б) Фурье-компонента на частоте тактового генератора создается посредством задержки и умножения. Длительность задержки, показанной на рис.2, б, равна половине периода передачи бита, и это значение является оптимальным, поскольку оно дает наибольшую Фурье-компоненту [20]. Сигнал m(t) всегда будет положительным во второй половине любого периода передачи бита, не будет иметь отрицательную первую половину, если во входном потоке битов s(t) произошло изменение состояния. Это дает прямоугольный сигнал, спектральные компоненты и все гармоники которого совпадают с теми, что были у сигнала в схеме на рис.2, а. Как и ранее, нужный спектральный компонент может быть отделен с помощью полосового фильтра, и ему будет придана нужная форма.

Последний пример (рис.2, в) соответствует контурному детектору. Основными операциями здесь являются дифференцирование и спрямление (посредством использования квадратичного устройства). Если на вход поступает сигнал прямоугольной формы, дифференциатор дает положительные или отрицательные пики на всех переходах символов. При спрямлении получаемая последовательность положительных импульсов будет давать Фурье-компоненту на скорости передачи информационных символов. Потенциально проблемой данной схемы является то, что дифференциаторы обычно весьма чувствительны к широкополосному шуму. Это делает необходимым введение перед дифференциатором фильтра нижних частот (low-pass filter — LPF), как показано на рис.2, в. В то ж время данный фильтр удаляет высокочастотные составляющие информационных символов, что приводит к потере сигналом исходной прямоугольной формы. Это, в свою очередь, приводит к тому, что результирующий дифференциальный сигнал будет иметь конечные времена нарастания и спада и уже не будет последовательностью импульсов.

Очевидно, что с этапами обработки сигналов, изображенными на рис.2, будет связана некоторая аппаратная задержка. В работе [12] показано, что для полосового фильтра, эффективно усредняющего К входных символов (ширина полосы = 1/КТ), величина среднего сбоя времени (задержки) приблизительно описывается следующим выражением

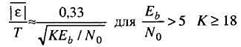(6)

Здесь Т — период передачи символа, Е_b — обнаруженная энергия на бит, a N₀ — односторонняя спектральная плотность мощности принятого шума. Там же показано, что при высоких отношениях сигнал/шум отношение среднеквадратического отклонения временной ошибки дается следующим выражением

(7)

Таким образом, если для данного полосового фильтра принятое отношение сигнал/шум достаточно велико, все методы, приведенные на рис.2, приведут к точной битовой синхронизации.

Дата добавления: 2014-11-08