Моделирование сверточных кодов в среде Матлаб

Сверточное кодирование - особый случай помехоустойчивого кодирования. В отличие от этого кодер блока, сверточный кодер не устройство, не имеющее памяти. Даже при том, что сверточный кодер принимает постоянное число символов сообщения и производит постоянное число кодовых символов, его вычисления зависят не только от текущего набора входных символов, но и на некоторых из предыдущих входных символов.

Откройте библиотеку Error Detection and Correction, щелкая два раза по его символу в главном Communications Blockset. Откройте подбиблиотеку Сверточный, щелкая два раза по его символу в библиотеке Error Detection and Correction.

Особенности сверточного кодирования. Библиотека Communications Blockset поддерживает разомкнутые или бинарные замкнутые коды, которые могут быть описаны структурой решетки или рядом порождающих полиномов.

Это использует алгоритм Viterbi, чтобы осуществить жесткое и мягкое декодирование.

Библиотека также включает декодер, максимизирующий апостериорную вероятность, который может использоваться для мягкого декодирования сверточных кодов.

Параметры сверточного кодирования. Процессы сверточного кодирования используют блоки Convolutional Encoder, Viterbi Decoder, и/или APP Decoder из библиотеки Convolutional. Если параметр маски требуется и в кодирующем устройстве и в декодере, используйте одно и то же значение в обоих блоках.

Блоки в подбиблиотеке Convolutional предполагают, что Вы используете один из двух различных представлений сверточного кодера:

· если, Вы проектируете свое кодирующее устройство, используя диаграмму со сдвиговыми регистрами и сумматорами по модулю 2, Вы можете вычислить порождающую полиномиальную матрицу кода и впоследствии использовать функцию poly2trellis (из Communications Toolbox), чтобы произвести соответствующую решетчатую (trellis) диаграмму маски параметра автоматически.

· Если Вы проектируете свое кодирующее устройство, используя решетчатую диаграмму, Вы можете построить решетчатую (trellis) диаграмму в MATLAB и использовать его в качестве параметра маски.

Использование полиномиального описания в блоках. Для использования полиномиального описания в блоках Convolutional Encoder, Viterbi Decoder, или APP Decoder используйте сервисную функцию poly2trellis из Communications Toolbox. Эта функция принимает полиномиальное описание и преобразовывает это в решетчатое описание. Например, следующая команда вычисляет решетчатое описание кодирующего устройства, длина ограничения которого равна 5 и чьи порождающие полиномы 35 и 31:

trellis = poly2trellis (5, [35 31]);

Использовать это кодирующее устройство с одним из блоков сверточного кодирования, просто поместите команду poly2trellis, таким образом

poly2trellis (5, [35 31]);

в поле параметров Trellis structure.

Пример: Разомкнутый кодер с кодовой скоростью 2/3. Этот пример использует разомкнутое сверточное кодирующее устройство со скоростью 2/3, изображенное на следующем рисунке. Описание объясняет, как определить параметры кодирующих блоков схемы разомкнутого кодирующего устройства со скоростью 2/3. Этот пример также иллюстрирует использование блока Error Rate Calculation с восстановлением задержки.

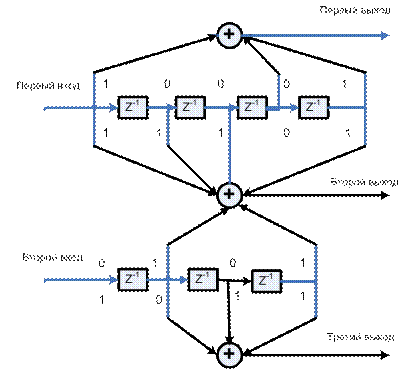
Определение параметров кодирования. Блоки Convolutional Encoder и Viterbi Decoder могут осуществить этот код, если у их параметров установлены соответствующие значения.

Длина ограничения кодирующего устройства - вектор длины 2, поэтому кодирующее устройство имеет два входа. Элементы этого вектора указывают на число сохраненных битов

в каждом сдвиговом регистре, включая текущие входные биты. Подсчет ячеек памяти в каждом сдвиговом регистре на диаграмме и добавлении того для текущих входов приводят к длине ограничения, равного [5 4].

Определяя порождающую матрицу кода как матрицу размера 2 Х 3 восьмеричных числа, используйте элемент в i – ой строке и j – ом столбце, чтобы указать, как i - ый вход воздействует на j – ый выход. Например, чтобы вычислить элемент во второй строке и третьем столбце, заметьте, что крайнее левое и два самых правых элемента во втором сдвиговом регистре диаграммы влияют на сумму, что формирует третий выход. Эта информация в двоичном коде равна 1011, что эквивалентно восьмеричному числу 13. Полная порождающая матрица кода равна [27 33 0; 0 5 13].

Для использования длины кодового ограничения и параметров порождающей матрицы кода в блоках Convolutional Encoder and Viterbi Decoder, примените функцию poly2trellis, чтобы преобразовать эти параметры в решеточную диаграмму.

Моделирование кодера. На рисунке представлена модель кодирующего устройства.

Чтобы построить модель, соберите и конфигурируйте блоки.

1. Блок Bernoulli Binary Generator из библиотеки Comm Sources.
• Установите параметр Probability of a zero, равным 0,5;
• Установите параметр Initial seed, равным положительному целому числу, предпочтительно выходу функции randseed;
• Установите параметр Sample time, равным 0,5;
• Установите флажок Frame-based outputs;
• Установите параметр Samples per frame, равным 2.
2. Блок Convolutional Encoder
• Установите параметр в состояние poly2trellis([54],[23 35 0; 0 5 13]).

3. Блок Binary Symmetric Channel из библиотеки Channels

· Установите параметр Error probability, равным 0.02;

· Установите параметр Initial seed, равным положительному целому числу, предпочтительно выходу функции randseed;

· Уберите флажок Output error vector.

4. Блок Viterbi Decoder.

· Установите параметр Trellis structure в poly2trellis([5 4],[23 35 0; 0 5 13]);

· Установите параметр Decision type в состояние Hard Decision.

5. Блок Error Rate Calculation из библиотеки Comm Sinks.

· Установите параметр Receive delay, равным 68;

· Установите параметр Output data в состояние Port;

· Установите флажок Stop simulation;

· Установите параметр Target number of errors, равным 100.

6. Блок Display из библиотеки Simulink Sinks

· Потяните базовый край символа, чтобы сделать показ, достаточно большим для трех записей.

Соедините блоки как на рисунке. Из меню Simulation, выберите Configuration parameters. В диалоговом окне установите параметр Stop time, равным inf.

Аннотации по размерам матрицы появляются на соединительных линиях, только если Вы выберете параметр Signal Dimensions подменю Port/signal displays из меню Format модели. Кодирующее устройство принимает вектор кадра размера 2 х 1 и производит вектор кадра размера 3 х 1, в то время как декодер делает обратное. Параметр Samples per frame parameter в блоке Bernoulli Binary Generator принят равным 2, потому что блок должен произвести слово сообщения длины 2.

Параметр Receive delay в блоке Error Rate Calculation принят равным 68, который является длиной вектора (2) восстановленного сообщения значения Traceback depth (34) в блоке Viterbi Decoder. Если Вы исследуете переданные и полученные сигналы, как матрицы в рабочем пространстве MATLAB, Вы видите, что первые 34 строки восстановленного сообщения состоят из нолей, в то время как последующие ряды - расшифрованные сообщения. Таким образом, задержка полученного сигнала - 34 вектора длины 2, или 68 отсчетов.

Запуск модели производит выход дисплея, состоящий из трех чисел: скорость роста ошибок, общее количество ошибок и общее количество ошибок сравнений, которые делает блок Error Rate Calculation во время моделирования. (Первое два числа изменяются в зависимости от Ваших значений Initial seed в блоках Bernoulli Binary Generator и Binary Symmetric Channel). Остановка моделирования после 100 ошибок происходят, потому что параметр Target number of errors установлен равным 100 в блоке Error Rate Calculation. Скорость роста ошибки должна быть меньше 0,02, как Error probability в блоке Binary Symmetric Channel.

Выполнение систематического кодирования с обратной связью. В этой секции объясняется, как использовать блок Convolutional Encoder для осуществления систематического кодирования с обратной связью. Код является систематическим, если фактические слова сообщения появляются как часть кодовых слов. Следующая диаграмма показывает пример систематического кодирующего устройства.

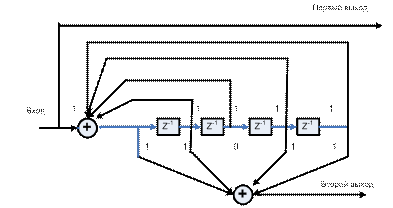
Чтобы осуществить это кодирующее устройство, установите параметр Trellis structure в блоке Convolutional Encoder в состояние к poly2trellis (5, [37 33], 37). Это соответствует:

· Кодовому ограничению длиной 5;

· Порождающей полиномиальной паре [37 33];

· полиному обратной связи: 37.

Полином обратной связи представлен двоичным вектором [1 1 1 11], соответствуя верхней строке двоичных цифр. Эти цифры указывают на связь выходов регистров с сумматором. Начальное значение 1 соответствует входному биту. Восьмеричное представление двоичного числа 11111 - 37.

Чтобы осуществить систематическое кодирование, установите первый порождающий полином в качестве полинома обратной связи в параметре Trellis structure блока Convolutional Encoder. В этом примере оба полинома имеют восьмеричное представление 37.

Второй порождающий полином представлен двойным вектором [1 1 0 1 1], соответствуя более нижнему ряду двоичных цифр. Восьмеричное число, соответствующее двоичному числу 11011 есть 33.

Пример мягкого декодирования. Моделирование создает случайный сигнал двоичного сообщения, кодирует сообщение в сверточный код, модулирует код, используя двоичную манипуляцию со смещением фазы, (BPSK) и добавляет белый Гауссовский шум к модулированному сигналу, чтобы моделировать шум канала. Тогда, моделирование готовит полученную информацию для блока декодирования. Наконец, моделирование сравнивает декодированную информацию с сигналом исходного сообщения, чтобы вычислить скорость роста ошибок. Конец моделирования наступает после обработки 100 битов ошибок или 10⁷ битов сообщения, после прибытия первого.

Определение сверточного кода. Разомкнутое сверточное кодирующее устройство в этом примере изображено ниже.

Длина ограничения кодирующего устройства - скаляр, так как у кодирующего устройства есть один вход. Значение длины ограничения - число битов, сохраненных в сдвиговом регистре, включая текущий вход. Есть шесть регистров памяти, и текущий вход составляет один бит. Таким образом, длина ограничения кода - 7.

Кодовый генератор является матрицей размера 1 х 2 матрица восьмеричных чисел, потому что кодирующее устройство имеет вход и два выхода. Первый элемент в матрице указывает на значение входа, влияющего на первый выход, и второй элемент в матрице указывает, на значение входа, влияющего на второй выход.

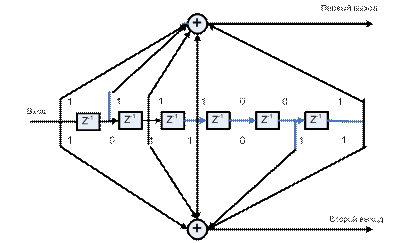
Например, первый выход в диаграмме кодирующего устройства – сумма по модулю 2 самого правого и четырех крайних левых элементов в массиве входных значений диаграммы. Двоичное число с семью цифрами 1111001 отражает эту информацию и эквивалентно восьмеричному числу 171. Восьмеричное число 171, таким образом, становится первым входом порождающей кодовой матрицы. Здесь, каждая тройка использует крайний левый бит как самый существенный бит. Второй выход соответствует двоичному числу 1011011, который эквивалентен восьмеричному номеру 133. Порождающий генератор кода поэтому [171 133].

Параметр Trellis structure в блоке Convolutional Encoder говорит о том, какой блок, кодирует, когда поступают данные. В этом случай, функция poly2trellis, в Communications Toolbox, преобразовывает длину кодового ограничения и пару восьмеричных чисел в решетчатую диаграмму.

В то время как данные о сообщении, входящие в блок Convolutional Encoder, являются скалярным потоком битов, закодированные данные являются потоком бинарных векторов длиной 2.

Карта полученных данных. Полученные данные, то есть, выход блока Convolutional Encoder, состоят из комплексных чисел, которые находятся в диапазоне между -1 и 1. Чтобы восстановить оригинальное двоичное сообщение, приемная часть модели должна декодировать сверточный код. Блок Viterbi Decoder в этой модели ожидает, что ее входные данные будут целые числа между 0 и 7. Демодулятор, обычная подсистема в этой модели, преобразовывает полученные данные в формат, который блок Viterbi Decoder может интерпретировать должным образом. Более определенно, подсистема демодулятора:

· Конвертирует полученные данные в реальный сигнал, удаляя его мнимую часть. Разумно предположить, что мнимая часть полученных данных не содержит существенную информацию, потому что мнимая часть переданных данных – есть ноль (игнорирование малых ошибок округления) и потому что шум канала не очень мощный.

· Нормализует полученные данные, деля на его текущее стандартное отклонение и затем умножая на -1.

• Квантует нормализованные данные, используя три бита.

Комбинация этой карты и решения карты блока Viterbi Decoder полностью изменяет модуляцию BPSK, чтобы блок BPSK Modulator Baseband выступил на передающей стороне этой модели.

Декодирование сверточного кода. После получения данных должным образом нанесенных на карту векторов длиной 2 3-битовых значений решения, блок Viterbi Decoder декодирует его. Блок использует алгоритм мягкого декодирования с 2³ различными входами потому, что параметр Decision type - есть Soft Decision и параметр Number of soft decision bits равен 3.

Интерпретация данных мягкого решения. Когда параметры Decision type установлен в состояние Soft Decision, блок Viterbi Decoder требует входных значений между 0 и 2^b-1, где b – есть параметр Number of soft decision bits. Блок интерпретирует 0 как самое достоверное решение того, что бит кодового слова, является 0 и интерпретирует 2^b-1 как самое достоверное решение того, что бит кодового слова, является 1. Значения между этими крайностями представляют менее достоверные решения. Следующая таблица перечисляет интерпретации восьми возможных входных значений для этого примера.

Значение решения	Интерпретация
	Наиболее уверенный 0
	Второй наиболее уверенный 0
	Третий наиболее уверенный 0
	Наименее уверенный 0
	Наименее уверенный 1
	Третий наиболее уверенный 1
	Второй наиболее уверенный 1
	Наиболее уверенный 1

Параметр Traceback depth в блоке Viterbi Decoder представляет длину задержки декодирования. Типичные значения для глубины traceback - приблизительно пять или шесть значений длины ограничения, которая была бы 35 или 42 в этом примере. Однако, некоторые варианты аппаратных средств предлагают варианты из 48 и 96. Этот пример выбирает 48, потому что это ближе к целям (35 и 42) чем 96.

Задержка полученных данных. Параметр Receive delay блока Error Rate Calculation является отличным от нуля, потому что бит данного сообщения и его соответствующий восстановленный бит, отделены во времени ненулевой суммой времени моделирования. Параметр Receive delay говорит, что элементы входных сигналов блока сравниваются, проверяя на ошибки.

В этом случае, значение Receive delay - 49 отсчетов, которое является большим на единицу, чем значение Traceback depth (48) в блоке Viterbi Decoder. Дополнительная задержка в один отсчет прибывает из начальной задержки блока Buffer. Поскольку блок Buffer должен собрать два скалярных отсчета прежде, чем выход сможет произвести один вектор, его первая значащий выход происходит во время 1 секунда, не время 0.

Сравнение результатов моделирования с теоретическими результатами. Эта секция описывает, как сравнить частоту появления ошибочных битов в этом моделировании с частотой появления ошибочных битов, которая теоретически следовала бы из неквантованного декодирования. Процесс включает несколько шагов, описанных в этих разделах.

Вычисление теоретических границы для частоты появления ошибочных битов. Для вычисления теоретических границ для частоты появления ошибочных битов P_b сверточного кодирования в этой модели, Вы можете использовать эту оценку, основанную на неквантованном решении декодирования:

В этой оценке c_d - сумма ошибок символов для ошибочных событий расстояния d и f - свободное расстояние кода. Величина P_d - попарная ошибочная вероятность, равная

где R - кодовый уровень 1/2, и erfc - дополнительная функция ошибок MATLAB, определенный в соответствии

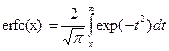
Значения для коэффициентов c_d и свободного расстояния f находится в опубликованных статьях такой как [4]. Свободное расстояние для этого кода - f = 10.

Следующие команды вычисляют значение для E_b/N₀ в диапазоне от 1 до 3.5, в приращениях 0.5:

Многократное моделирование для сбора частоты появления ошибочных битов. Вы можете эффективно изменить параметры моделирования при использовании функции sim, чтобы управлять моделированием из командной строки MATLAB. Например, следующий программный код вычисляет скорость роста битовых ошибок в отношениях битовой энергии к шуму в пределах от 1 децибела до 4 децибел, в приращениях по 0.5 децибелов. Он собирает все частоты появления ошибочных битов при этих запусках моделирования в матричной функции BERVec. Он также изображает рисунок для частоты появления ошибочных битов наряду с теоретическими границами, вычисленными в предыдущем кодовом фрагменте.

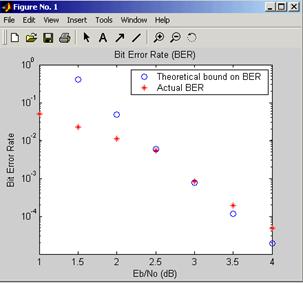
Оценка для P_b принимает то, что декодер использует неквантованные данные, то есть, бесконечно частое квантование. В отличие от этого, моделирование в этом примере использует (3-битовое) квантование на 8 уровнях. Из-за этого квантования моделируемая частота появления ошибочных битов не так низка, как граница, когда отношение сигнал-шум высоко.

График частоты появления ошибочных битов в зависимости от отношения сигнал-шум следует. Местоположения Ваших фактических точек BER могли бы измениться, потому что моделирование использует случайные числа.

Дата добавления: 2014-11-08