Людвиг Бьорне 1 страница

Выводы

Задача о диете.

Задача об определении надежности электрической цепи.

Задача о нахождении связи между структурой и свойствами веществ.

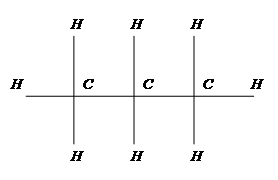Рассмотрим несколько химических соединений, называемых нормальными алканами. Они состоят из п атомов углерода и п + 2 атомов водорода (п = 1, 2, …), связанных между собой так, как показано на рисунке 7.3 для п = 3. Пусть известны экспериментальные значения температур кипения этих соединений: у_э(3) = -42⁰, у_э(4) = 0⁰, у_э(5) = 28⁰, у_э(6) = 69⁰.

Требуется найти приближенную зависимость между температурой кипения и числом п для этих соединений.

Рисунок 7.3

1. Построение модели. Предположим, что эта зависимость имеет вид 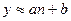, где а и b – константы, подлежащие определению. Для нахождения а и b подставим в эту формулу последовательно п = 3, 4, 5, 6 и соответствующие значения температур кипения. Имеем: -42» 3 а + b, 0» 4 а + b, 28» 5 а + b, 69» 6 а + b.

2. Решение математической задачи, к которой приводит модель. Для определения наилучших а и b существует много различных методов. Воспользуемся наиболее простым из них. Выразим b через а из этих уравнений: b» -42 – 3 a, b» – 4 a, b» 28 – 5 a, b» 69 – 6 a. Возьмем в качестве искомого b среднее арифметическое этих значений, то есть, положим b» 16 – 4,5 a. Подставим в исходим в исходную систему уравнений это значение b и, вычисляя а, получим для а следующие значения: а» 37, а» 28, а» 28, а» 36. Возьмем в качестве искомого а среднее значение этих чисел, то есть положим а» 34. Итак, искомое уравнение имеет вид: .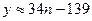

4. Проверка адекватности модели. Проверим точность модели на исходных четырех соединениях, для чего вычислим температуры кипения по полученной формуле: у_р(3) = -37⁰, у_р(4) = -3⁰, у_р(5) = 31⁰, у_р(6) = 65⁰. Таким образом, ошибка расчетов данного свойства для этих соединений не превышает 5⁰. Используем полученное уравнение для расчета температуры кипения соединения с п = 7, не входящего в исходное множество, для чего подставим в это уравнение п = 7: у_р(7) = 99⁰. Результат получился довольно точный: известно, что экспериментальное значение температуры кипения у_э(7) = 98⁰.

Здесь мы рассмотрим пример вероятностной модели (основные понятия теории вероятностей находятся в теоретическом разделе 5 темы).

Предположим, что в электрическую цепь последовательно включены три элемента, работающие независимо друг от друга. Вероятности отказов 1-го, 2-го и 3-го элементов соответственно равны Р₁ = 0,1, Р₂ = 0,15, Р₃ = 0,2. Будем считать цепь надежной, если вероятность того, что в цепи не будет тока, не более 0,4. Требуется определить, является ли цепь надежной.

1. Построение модели. Так как элементы включены последовательно, то тока в цепи не будет, если откажет хотя бы один из элементов.

Пусть А – событие, состоящее в том, что тока в цепи не будет; событие А_i (i = 1, 2, 3) заключается в том, что i -тый элемент работает. Тогда Р(А₁) = 1 – 0,1 = 0,9, Р(А₂) = 1- 0,15 = 0,85, Р(А₃) = 1 – 0,2 = 0,8. Очевидно, что событие, состоящее в том, что по цепи проходит ток, равно событию, заключающемуся в том, что все три элемента работают, т.е. равно произведению трех независимых событий А₁, А₂ и А₃ (наступление каждого из этих событий не зависит от наступления двух других).

2. Решение математической задачи, к которой приводит модель. По теореме о вероятности произведения независимых событий Р(А₁А₂А₃) = Р(А₁)Р(А₂)Р(А₃) = 0,9·0,85 ·0,8 = 0,612. Тогда Р(А) + Р(А₁А₂А₃) = 1. Поэтому Р(А) = 1 – 0,612 = 0,388 < 0,4.

3. Интерпретация полученных следствий из математической модели. Р(А) = 0,388 < 0,4. Следовательно, цепь является надежной.

Дама просто приятная решила похудеть и, как это нередко случается, обратилась за советом к подруге. Подруга – дама приятная во всех отношениях, посоветовала ей перейти на рациональное питание, состоящее из двух новомодных продуктов Р и Q.

Дневное питание этими новинками должно давать не более 14 единиц жира (чтобы похудеть), но и не менее 300 калорий (чтобы не сойти с дистанции раньше). На банке с продуктом Р написано, что в одном килограмме этого продукта содержится 15 единиц жира и 150 калорий, а на банке с продуктом Q – 4 единицы жира и 200 калорий соответственно. При этом цена 1 кг продукта Р равна 15 у.е., а 1 кг продукта Q – 25 у.е.

Так как дама просто приятная в это время была несколько стеснена в средствах, то ее интересовал ответ на следующий вопрос: в какой пропорции нужно брать эти удивительные продукты Р и Q для того, чтобы выдержать условия диеты и истратить как можно меньше денег?

1. Построение модели. Обозначим через х количество продукта Р, а через у – количество продукта Q, требуемые для выполнения условий диеты.

Количество единиц жира, содержащегося в х кг продукта Р и в у кг продукта Q, равно 15 х + 4 у и по условию диеты не должно превосходить 14. Поэтому .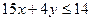

В свою очередь, количество калорий, содержащихся в х кг продукта Р и в у кг продукта Q, равно 150 х + 200 у и должно быть не меньше 300. Значит, .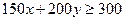

Теперь о стоимости продуктов. Она равна z(х; у) = 15x + 25y и в соответствии с высказанными пожеланиями должна быть минимальной. Последнее записывается так: z(х; у) = 15x + 25y → min.

Итак, мы получили систему неравенств

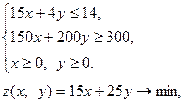
которая является математической моделью задачи.

Полученная система неравенств называется системой ограничений задачи, а функция z(х; у) называется целевой функцией задачи.

2. Решение математической задачи, к которой приводит модель. Для решения применим координатно-графический метод.

Решением системы ограничений является многоугольник, полученный путем пересечения областей решений всех неравенств системы. Решением линейного неравенства является одна из полуплоскостей, на которые прямая, соответствующая данному неравенству, делит координатную плоскость. Для определения искомой полуплоскости берется точка, не лежащая на прямой, ее координаты подставляются в неравенство. Если в результате получается верное числовое неравенство, то решением является полуплоскость, содержащая выбранную точку. В противном случае, решением является другая полуплоскость.

Введем на плоскости прямоугольную систему координат хОу и построим многоугольник решений системы ограничений нашей задачи.

Из условий х ≥ 0 и у ≥ 0 вытекает, что все точки, которые удовлетворяют системе ограничений, лежат в первой координатной четверти.

Теперь решим неравенство 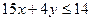. Ему соответствует прямая, заданная уравнением 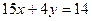, которая проходит через точк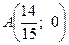и и 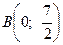. Для проверки возьмем точку О(0; 0): 15 · 0 + 4 · 0 = 0 ≤ 14. Так как 0 ≤ 14 – верное неравенство, то решением неравенства 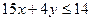является полуплоскость, содержащая точку О.

Обращаясь подобным же образом с неравенством 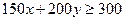, находим точки пересечения прямой 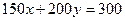с осями координат – точки С(2; 0) и D(0; 1,5). Для проверки также возьмем точку О(0; 0): 150 · 0 + 200 · 0 = 0 ≥ 300. Так как 0 ≥ 300 – неверное числовое неравенство, то решением неравенства 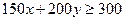является полуплоскость, не содержащая точку О.

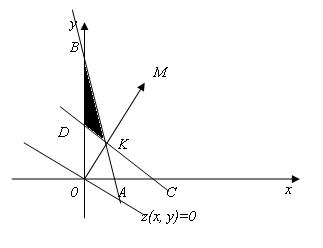
Рисунок 7.4

Пересечением всех полуплоскостей является треугольник BDK (рис. 7.4). Точка К является точкой пересечения прямых АВ и CD и имеет координаты .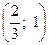

Теперь среди всех точек треугольника найдем ту, координаты которой удовлетворяют условию минимальности целевой функции z.

Для этого построим так называемую линию нулевого уровня функции z, которая задается уравнением z(x; y) = 0. Будем двигать эту прямую в направлении вектора 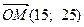, координатами которого являются соответствующие коэффициенты целевой функции, до места первой встречи этой прямой с треугольником BDK. Искомой точкой будет точка К 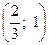. То есть искомые значения х = 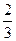, у = 1.

3. Интерпретация полученных следствий из математической модели. Таким образом, чтобы выполнить условия диеты и истратить при этом как можно меньше средств, продукты Р и Q нужно брать в отношении х: у = 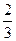: 1 = 2: 3. То есть на 2 части продукта Р брать 3 части продукта Q.

Модель – это условный образ объекта, построенный для упрощения его исследования.

Конечно, при попытке упрощенного описания ситуации некоторыми обстоятельствами приходится пренебрегать, считая их несущественными. Однако единого взгляда на то, что именно существенно, а что не очень, по-видимому, нет. Можно, например, не обращать внимания на то, что начался дождик. Но одно дело пробежать под накрапывающим дождем сотню метров, и совсем другое – часовая прогулка под таким дождем без зонта.

Предлагая построенную или выбранную нами модель, мы непременно должны указывать пределы, в которых ею можно пользоваться, и предупреждать о том, что нарушение этих ограничений приводит (и, скорее всего, приведет) к серьезным ошибкам. Коротко говоря, у каждой модели есть свой ресурс.

Покупая блузку или рубашку, мы привыкли к наличию меток, на которых указаны максимально допустимая температура глажения, дозволенные виды стирки и т.п. Это, конечно, ни в коей мере не означает, что нам запрещается, взяв докрасна раскаленный утюг, пройтись им по ткани раз-другой. Такое мы сделать можем. Но вот захотим ли мы носить блузку или рубашку после такого глажения?

Таким образом, построение модели опирается на значительное упрощение изучаемой ситуации и, следовательно, к получаемым на ее основе выводам нужно относиться достаточно осторожно – модель может не все.

Вместе с тем, даже весьма грубая на вид идеализация нередко позволяет глубже вникнуть в суть проблемы. Пробуя как-то влиять на параметры модели (выбирать их, управлять ими), мы получаем возможность подвергнуть исследуемое явление качественному анализу и сделать выводы общего характера.

Контрольные вопросы

1 Что такое модель, моделирование?

2 Какие два подхода различают в моделировании? В чем их особенность?

3 Перечислите типы моделей. Дайте им краткую характеристику.

4 В чем важность математического моделирования?

5 Перечислите этапы математического моделирования. Охарактеризуйте каждый этап.

6 Как можно классифицировать математические модели?

7 Приведите пример задачи математического моделирования.

8 Почему нужно с осторожностью относиться к выводам, полученным на основе модели?

Тема 8: Элементы истории математики

После открытия своей знаменитой теоремы Пифагор принес в жертву сто быков. С тех пор каждый раз, когда совершается открытие, крупный рогатый скот начинает волноваться.

Самой древней математической деятельностью являлся счет. Счет был необходим, чтобы следить за поголовьем скота и вести торговлю. Некоторые первобытные племена подсчитывали количество предметов, сопоставляя им различные части тела, главным образом пальцы рук и ног. Наскальный рисунок каменного века, сохранившийся до наших времен, изображает число 35 в виде серии выстроенных в ряд 35 палочек-пальцев. Первыми существенными успехами в арифметике стали концептуализация числа и изобретение четырех основных действий: сложения, вычитания, умножения и деления. Первые достижения геометрии связаны с такими простыми понятиями, как прямая и окружность. Дальнейшее развитие математики началось примерно в 3000 г. до н. э. благодаря вавилонянам и египтянам.

Вавилония и Египет

Вавилония

Источником наших знаний о вавилонской цивилизации служат хорошо сохранившиеся глиняные таблички, покрытые так называемыми клинописными текстами, которые датируются от 2000 г. до н. э. и до 300 г. н. э. Математика на клинописных табличках в основном была связана с ведением хозяйства. Арифметика и нехитрая алгебра использовались при обмене денег и расчетах за товары, вычислении простых и сложных процентов, налогов и доли урожая, сдаваемой в пользу государства, храма или землевладельца. Многочисленные арифметические и геометрические задачи возникали в связи со строительством каналов, зернохранилищ и другими общественными работами. Очень важной задачей математики был расчет календаря, поскольку календарь использовался для определения сроков сельскохозяйственных работ и религиозных праздников. Деление окружности на 360, а градуса и минуты на 60 частей берут начало в вавилонской астрономии.

Вавилоняне создали и систему счисления, использовавшую для чисел от 1 до 59 основание 10. Символ, обозначавший единицу, повторялся нужное количество раз для чисел от 1 до 9. Для обозначения чисел от 11 до 59 вавилоняне использовали комбинацию символа числа 10 и символа единицы. Для обозначения чисел от 60 и больше вавилоняне ввели позиционную систему счисления с основанием 60. Существенным продвижением стал позиционный принцип, согласно которому один и тот же числовой знак (символ) имеет различные значения в зависимости от того места, где он расположен. Примером могут служить значения шестерки в записи (современной) числа 606. Однако нуль в системе счисления древних вавилонян отсутствовал, из-за чего один и тот же набор символов мог означать и число 65 (60 + 5), и число 3605 (60² + 0 + 5). Возникали неоднозначности и в трактовке дробей. Например, одни и те же символы могли означать и число 21, и дробь 21/60 и (20/60 + 1/60²). Неоднозначность разрешалась в зависимости от конкретного контекста.

Вавилоняне составили таблицы обратных чисел (которые использовались при выполнении деления), таблицы квадратов и квадратных корней, а также таблицы кубов и кубических корней. Им было известно приближение числа. Клинописные тексты, посвященные решению алгебраических и геометрических задач, свидетельствуют о том, что вавилоняне пользовались квадратичной формулой для решения квадратных уравнений и могли решать некоторые специальные типы задач, включавших до десяти уравнений с десятью неизвестными, а также отдельные разновидности кубических уравнений и уравнений четвертой степени. На глиняных табличках запечатлены только задачи и основные шаги процедур их решения. Так как для обозначения неизвестных величин использовалась геометрическая терминология, то и методы решения в основном заключались в геометрических действиях с линиями и площадями. Что касается алгебраических задач, то они формулировались и решались в словесных обозначениях.

Около 700 г. до н. э. вавилоняне стали применять математику для исследования движений Луны и планет. Это позволило им предсказывать положения планет, что было важно как для астрологии, так и для астрономии.

В геометрии вавилоняне знали о таких соотношениях, например, как пропорциональность соответствующих сторон подобных треугольников. Им была известна теорема Пифагора и то, что угол, вписанный в полуокружность, – прямой. Они располагали также правилами вычисления площадей простых плоских фигур, в том числе правильных многоугольников, и объемов простых тел. Число p вавилоняне считали равным 3.

Египет

Наше знание древнеегипетской математики основано, главным образом, на двух папирусах, датируемых примерно 1700 г. до н. э. Излагаемые в этих папирусах математические сведения восходят к еще более раннему периоду – около 3500 г. до н. э. Египтяне использовали математику, чтобы вычислять вес тел, площади посевов и объемы зернохранилищ, размеры податей и количество камней, требуемое для возведения тех или иных сооружений. В папирусах можно найти также задачи, связанные с определением количества зерна, необходимого для приготовления заданного числа кружек пива, а также более сложные задачи, связанные с различием в сортах зерна; для этих случаев вычислялись переводные коэффициенты.

Но главной областью применения математики была астрономия, точнее, расчеты, связанные с календарем. Календарь использовался для определения дат религиозных праздников и предсказания ежегодных разливов Нила. Однако уровень развития астрономии в Древнем Египте намного уступал уровню ее развития в Вавилоне.

Древнеегипетская письменность основывалась на иероглифах. Система счисления того периода также уступала вавилонской. Египтяне пользовались непозиционной десятичной системой, в которой числа от 1 до 9 обозначались соответствующим числом вертикальных черточек, а для последовательных степеней числа 10 вводились индивидуальные символы. Последовательно комбинируя эти символы, можно было записать любое число. С появлением папируса возникло так называемое иератическое письмо-скоропись, способствовавшее появлению новой числовой системы. Для каждого из чисел от 1 до 9 и для каждого из первых девяти кратных чисел 10, 100 и т. д. использовался специальный опознавательный символ. Дроби записывались в виде суммы дробей с числителем, равным единице. С такими дробями египтяне производили все четыре арифметические операции, но процедура таких вычислений оставалась очень громоздкой.

Геометрия у египтян сводилась к вычислениям площадей прямоугольников, треугольников, трапеций, круга, а также формулам вычисления объемов некоторых тел. Надо сказать, что математика, которую египтяне использовали при строительстве пирамид, была простой и примитивной.

Задачи и решения, приведенные в папирусах, сформулированы чисто рецептурно, без каких бы то ни было объяснений. Египтяне имели дело только с простейшими типами квадратных уравнений и арифметической и геометрической прогрессиями, а потому и те общие правила, которые они смогли вывести, были также самого простейшего вида. Ни вавилонская, ни египетская математики не располагали общими методами; весь свод математических знаний представлял собой скопление эмпирических формул и правил.

Хотя майя, жившие в Центральной Америке, не оказали влияния на развитие математики, их достижения, относящиеся примерно к IV в., заслуживают внимания. Майя, по-видимому, первыми использовали специальный символ для обозначения нуля в своей двадцатеричной системе. У них были две системы счисления: в одной применялись иероглифы, а в другой, более распространенной, точка обозначала единицу, горизонтальная черта – число 5, а специальный символ обозначал нуль. Позиционные обозначения начинались с числа 20, а числа записывались по вертикали сверху вниз.

Греческая математика

Классическая Греция

С точки зрения XX в. родоначальниками математики явились греки классического периода (VI – IV вв. до н. э.). Математика, существовавшая в более ранний период, была набором эмпирических заключений. Напротив, в дедуктивном рассуждении новое утверждение выводится из принятых посылок способом, исключавшим возможность его неприятия.

Настаивание греков на дедуктивном доказательстве было экстраординарным шагом. Ни одна другая цивилизация не дошла до идеи получения заключений исключительно на основе дедуктивного рассуждения, исходящего из явно сформулированных аксиом. Одно из объяснений приверженности греков методам дедукции мы находим в устройстве греческого общества классического периода. Математики и философы (нередко это были одни и те же лица) принадлежали к высшим слоям общества, где любая практическая деятельность рассматривалась как недостойное занятие. Математики предпочитали абстрактные рассуждения о числах и пространственных отношениях решению практических задач. Математика делилась на арифметику – теоретический аспект и логистику – вычислительный аспект. Заниматься логистикой предоставляли свободнорожденным низших классов и рабам.

Греческая система счисления была основана на использовании букв алфавита. Аттическая система, бывшая в ходу с VI – III вв. до н. э., использовала для обозначения единицы вертикальную черту, а для обозначения чисел 5, 10, 100, 1000 и 10 000 – начальные буквы их греческих названий. В более поздней ионической системе счисления для обозначения чисел использовались 24 буквы греческого алфавита и три архаические буквы. Кратные 1000 до 9000 обозначались так же, как первые девять целых чисел от 1 до 9, но перед каждой буквой ставилась вертикальная черта. Десятки тысяч обозначались буквой М (от греческого «мириои» – 10 000), после которой ставилось то число, на которое нужно было умножить десять тысяч

Дедуктивный характер греческой математики полностью сформировался ко времени Платона и Аристотеля. Изобретение дедуктивной математики принято приписывать Фалесу Милетскому (ок. 640 – 546 гг. до н. э.), который, как и многие древнегреческие математики классического периода, был также философом. Высказывалось предположение, что Фалес использовал дедукцию для доказательства некоторых результатов в геометрии, хотя это сомнительно.

Другим великим греком, с чьим именем связывают развитие математики, был Пифагор (ок. 585 – 500 гг. до н. э.). Полагают, что он мог познакомиться с вавилонской и египетской математикой во время своих долгих странствий. Пифагор основал движение, расцвет которого приходится на период около 550 – 300 гг. до н. э. Пифагорейцы создали чистую математику в форме теории чисел и геометрии. Целые числа они представляли в виде конфигураций из точек или камешков, классифицируя эти числа в соответствии с формой возникающих фигур («фигурные числа»). Слово «калькуляция» (расчет, вычисление) берет начало от греческого слова, означающего «камешек». Числа 3, 6, 10 и т. д. пифагорейцы называли треугольными, так как соответствующее число камешков можно расположить в виде треугольника, числа 4, 9, 16 и т. д. — квадратными, так как соответствующее число камешков можно расположить в виде квадрата, и т. д.

Из простых геометрических конфигураций возникали некоторые свойства целых чисел. Например, пифагорейцы обнаружили, что сумма двух последовательных треугольных чисел всегда равна некоторому квадратному числу. Они открыли, что если (в современных обозначениях) n² – квадратное число, то n²+2n+1 = (n+1)². Число, равное сумме всех своих собственных делителей, кроме самого этого числа, пифагорейцы называли совершенным. Примерами совершенных чисел могут служить такие целые числа, как 6, 28 и 496. Два числа пифагорейцы называли дружественными, если каждое из чисел равно сумме делителей другого; например, 220 и 284 – дружественные числа (и здесь само число исключается из собственных делителей).

Для пифагорейцев любое число представляло собой нечто большее, чем количественную величину. Например, число 2, согласно их воззрению, означало различие и потому отождествлялось с мнением. Четверка представляла справедливость, так как это первое число, равное произведению двух одинаковых множителей.

Пифагорейцы также открыли, что сумма некоторых пар квадратных чисел есть снова квадратное число. Например, сумма 9 и 16 равна 25, а сумма 25 и 144 равна 169. Такие тройки чисел, как 3, 4 и 5 или 5, 12 и 13, называются пифагоровыми числами. Они имеют геометрическую интерпретацию: если два числа из тройки приравнять длинам катетов прямоугольного треугольника, то третье число будет равно длине его гипотенузы. Такая интерпретация, по-видимому, привела пифагорейцев к осознанию более общего факта, известного ныне под названием теоремы Пифагора, согласно которой в любом прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов.

Рассматривая прямоугольный треугольник с единичными катетами, пифагорейцы обнаружили, что длина его гипотенузы равна корню из двух, и это повергло их в смятение, ибо они тщетно пытались представить число в виде отношения двух целых чисел, что было крайне важно для их философии. Величины, непредставимые в виде отношения целых чисел, пифагорейцы назвали несоизмеримыми; современный термин – «иррациональные числа». Около 300 г. до н. э. Евклид доказал, что число 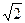несоизмеримо. Пифагорейцы имели дело с иррациональными числами, представляя все величины геометрическими образами. Если 1 и 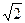считать длинами некоторых отрезков, то различие между рациональными и иррациональными числами сглаживается. Произведение чисел a и b есть площадь прямоугольника со сторонами длиной a и b. Мы и сегодня иногда говорим о числе 25 как о квадрате 5, а о числе 27 – как о кубе 3.

Древние греки решали уравнения с неизвестными посредством геометрических построений. Были разработаны специальные построения для выполнения сложения, вычитания, умножения и деления отрезков, извлечения квадратных корней из длин отрезков; ныне этот метод называется геометрической алгеброй.

Приведение задач к геометрическому виду имело ряд важных последствий. В частности, числа стали рассматриваться отдельно от геометрии, поскольку работать с несоизмеримыми отношениями можно было только с помощью геометрических методов. Геометрия стала основой почти всей строгой математики, по крайней мере, до 1600 г. И даже в XVIII в., когда уже были достаточно развиты алгебра и математический анализ, строгая математика трактовалась как геометрия, а слово «геометр» было равнозначно слову «математик».

Именно пифагорейцам мы во многом обязаны той математикой, которая затем была систематизированно изложена и доказана в «Началах» Евклида. Есть основания полагать следующее: именно они открыли то, что ныне известно как теоремы о треугольниках, параллельных прямых, многоугольниках, окружностях, сферах и правильных многогранниках.

Одним из самых выдающихся пифагорейцев был Платон (ок. 427 – 347 гг. до н. э.). Платон был убежден, что физический мир постижим лишь посредством математики. Считается, что именно ему принадлежит заслуга изобретения аналитического метода доказательства. Аналитический метод начинается с утверждения, которое требуется доказать, и затем из него последовательно выводятся следствия до тех пор, пока не будет достигнут какой-нибудь известный факт; доказательство получается с помощью обратной процедуры. Принято считать, что последователи Платона изобрели метод доказательства, получивший название «доказательство от противного». Заметное место в истории математики занимает Аристотель, ученик Платона. Аристотель заложил основы науки логики и высказал ряд идей относительно определений, аксиом, бесконечности и возможности геометрических построений.

Величайшим из греческих математиков классического периода, уступавшим по значимости полученных результатов только Архимеду, был Евдокс (ок. 408 – 355 гг. до н. э.). Именно он ввел понятие величины для таких объектов, как отрезки прямых и углы. Располагая понятием величины, Евдокс логически строго обосновал пифагорейский метод обращения с иррациональными числами.

Работы Евдокса позволили установить дедуктивную структуру математики на основе явно формулируемых аксиом. Ему же принадлежит и первый шаг в создании математического анализа, поскольку именно он изобрел метод вычисления площадей и объемов, получивший название «метода исчерпывания». Этот метод состоит в построении вписанных и описанных плоских фигур или пространственных тел, которые заполняют («исчерпывают») площадь или объем той фигуры или того тела, которое является предметом исследования. Евдоксу же принадлежит и первая астрономическая теория, объясняющая наблюдаемое движение планет. Предложенная Евдоксом теория была чисто математической; она показывала, каким образом комбинации вращающихся сфер с различными радиусами и осями вращения могут объяснить кажущиеся нерегулярными движения Солнца, Луны и планет.

Дата добавления: 2014-11-16