
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Вопросы к экзамену (зачету)
|
|
|
|
1. Какие понятия называют основными неопределяемыми понятиями?
2. Что значит определить понятие?
3. Что такое аксиома, теорема?
4. Какие требования предъявляются к системе аксиом?
5. Приведите 2-3 распространенных в литературе определения понятия «математика».
6. Какие аксиомы и постулаты привел Евклид в своих «Началах» в III в. до н.э.?
7. В чем заключается сущность аксиоматического метода?
8. Какое место занимает математика в системе других наук?
9. В чем важность математического образования?
10. Перечислите основные математические структуры. Чем они характеризуются?
11. Для чего математика нужна гуманитарию?
12. Перечислите недостатки системы аксиом Евклида.
13. Назовите геометрии, отличающиеся от геометрии Евклида. В чем состоит их отличие?
14. Назовите основателя теории множеств.
15. Дайте определение множества, элемента множества. Примеры.
16. Какие способы задания множеств вы знаете? Примеры.
17. Какие множества называют равными? Примеры.
18. Дайте определение подмножества. Чем отличаются собственные подмножества от несобственных? Примеры.
19. Какие множества называются числовыми? Приведите примеры числовых множеств.
20. Пересечение, и объединение множеств. Примеры.
21. Вычитание и дополнение множеств. Примеры.
22. Порядок выполнения операций над множествами. Примеры.
23. Как изображаются операции над множествами с помощью диаграмм Эйлера-Венна?
24. Перечислите свойства операций над множествами.
25. Для решения каких задач используют формулу Грассмана?
26. Дайте определение высказывания и высказывательной формы.
27. Перечислите основные логические связки.
28. Дайте определение логической операции.
29. Дайте определение негации, конъюнкции, дизъюнкции, импликации и эквиваленции.
30. Какие переменные называются пропозициональными?
31. Сформулируйте определение формулы логики высказываний.
32. Опишите процедуру формализации высказываний.
33. Для чего нужна таблица истинности?
34. Опишите алгоритм составления таблицы истинности.
35. Какие формулы называются тавтологиями, противоречиями, выполнимыми (опровержимыми)?
36. Какие формулы называются равносильными?
37. Сформулируйте несколько основных законов логики.
38. Для чего нужны законы логики?
39. Сформулируйте правило умножения. Примеры.
40. Что такое п- факториал? Примеры.
41. Что называется перестановками из п элементов? Примеры.
42. Какие комбинации называются размещениями? Примеры.
43. Какие комбинации называются сочетаниями? Примеры.
44. Запишите формулы для нахождения перестановок, размещений и сочетаний.
45. Сформулируйте правило сложения. Примеры.
46. Что называется испытанием? Примеры.
47. Как называется результат испытания? Примеры.
48. Какие виды событий бывают, чем они отличаются? Примеры.
49. Что такое статистическая вероятность события? Примеры.
50. Опишите классическую схему нахождения вероятности события. Примеры.
51. Сформулируйте определение классической вероятности события. Примеры.
52. Какие события называются противоположными? Примеры.
53. Чему равна вероятность достоверного события, невозможного события? Примеры.
54. Какие события называют несовместными? Примеры.
55. Как можно найти вероятность одного из двух противоположных событий? Примеры.
56. Какие события называются независимыми? Примеры.
57. Сформулируйте теоремы сложения и умножения вероятностей. Примеры.
58. Что такое математическая статистика? Чем она занимается?
59. Какие величины называют случайными? Когда случайную величину называют дискретной, а когда – непрерывной?
60. Что такое закон распределения дискретной случайной величины? Как он может быть задан?
61. Как задаются непрерывные случайные величины?
62. Что называется генеральной совокупностью, выборкой, вариантой, вариационным рядом?
63. Что такое частота варианты, мода, медиана, размах выборки?
64. Дайте определение математического ожидания случайной величины. Как найти математическое ожидание? Перечислите его свойства.
65. Дайте определение дисперсии случайной величины. Как она находится? Перечислите свойства дисперсии.
66. Что называется статистической устойчивостью и статистической вероятностью случайного события?
67. Что такое модель, моделирование?
68. Какие два подхода различают в моделировании? В чем их особенность?
69. Перечислите типы моделей. Дайте им краткую характеристику.
70. В чем важность математического моделирования?
71. Перечислите этапы математического моделирования. Охарактеризуйте каждый этап.
72. Как можно классифицировать математические модели?
73. Приведите пример задачи математического моделирования.
74. Почему нужно с осторожностью относиться к выводам, полученным на основе модели?
75. Математика древности. Вавилония и Египет.
76. Математика древности. Классическая Греция.
77. Математика древности. Греция. Александрийский период.
78. Математика древности. Индия и арабы.
79. Математика средних веков. Европа. Возрождение.
80. Начала современной математики. Алгебра.
81. Начала современной математики. Аналитическая геометрия.
82. Начала современной математики. Математический анализ.
83. Современная математика. Неевклидова геометрия.
84. Современная математика. Математическая строгость.
Контрольная работа для студентов факультета психологии, валеологии и спорта заочного отделения специальностей «Логопедия», «Олигофренопедагогика», «Адаптивная физкультура» и «Физическая культура и спорт»
Номер варианта определяется из таблицы по двум последним цифрам зачетной книжки. То есть, если две последние цифры зачетки (студенческого билета) 36, то студент должен решить задачи под номерами: 10, 13, 26, 39, 42, 55, 68.
Таблица
| Предпоследняя цифра зачетной книжки | Последняя цифра зачетной книжки | |||||||||
Продолжение таблицы
| Предпоследняя цифра зачетной книжки | Последняя цифра зачетной книжки | |||||||||
Контрольная работа оформляется в тетради в клеточку (12 листов). На титульном листе пишется название предмета (математика), фамилия, инициалы и номер группы студента, выполнившего работу.
Задания для контрольной работы
Задание 1: Даны множества: А и В. Найти: 1) А∩В; 2) АUВ; 3) А\В; 4) (АUВ)\(А∩В).
1. А = {12; 20; 34; 37}, В = {2; 34; 35; 37}.
2. А = {3; 5; 7;9}, В = {3; 7; 15; 28}.
3. А = {2; 4; 6; 8; 10}, В = {2; 4; 3; 1; 6}.
4. А = {1; 2; 3; 4; 5; 6}, В = {3; 2; 6; 8}.
5. А = {25; 37; 44; 56}, В = {13; 15; 37; 48}.
6. А = {2; 6; 20; 21; 35}, В = {4; 15; 21; 35}.
7. А = {2; 3; 6; 8; 10}, В = {1; 2; 4; 25; 33}.
8. А = {0; 1; 2; 3; 7; 15}, В = {-2; 0; 3; 2; 14}.
9. А = {-7; -3; 2; 4; 33}, В = {-1; 0; 1; 2; 4; 3}.
10. А = {2; 6; 24; 12; 31}, В = {0; 7; 13; 18; 31}.
Задание 2: Решить задачу, используя формулу Грассмана:
11. В детском саду 52 ребенка. Каждый из них любит пирожное или мороженое. 25 детей любит пирожное, а 20 человек – пирожное и мороженое. Сколько детей любит мороженое?
12. Из 220 школьников 163 играют в баскетбол, 175 – в футбол, 24 – не играют в эти игры. Сколько человек играют в баскетбол и футбол?
13. Каждый из членов команды играет либо в футбол, либо в теннис, либо в футбол и в теннис. Сколько человек в команде, если известно, что 18 человек играют в обе игры, 23 человека играют в футбол, 21 – в теннис?
14. В кружке мягкой игрушки занимается 26 человек. Половина детей любят карамель, а 10 человек – карамель и шоколадные конфеты. Сколько детей любят шоколадные конфеты?
15. В младшей группе детского сада 15 детей пьют молоко, 20 – кефир, 10 – и молоко, и кефир. Сколько детей в группе?
16. Все студенты в группе изучают английский или немецкий язык. 12 студентов изучают английский язык, 15 – немецкий, 3 – оба языка. Сколько студентов в группе?
17. Из 27 учеников 13 человек любят читать фантастику, 8 – приключенческую литературу и фантастику. Сколько человек любят читать приключенческую литературу?
18. В кружке вязания 14 девочек связали шапочку, 15 – шарф, 7 – шапочку и шарф. Сколько девочек ходит в кружок?
19. В старшей группе детского сада 22 ребенка. Половина детей любит манную кашу, а 8 человек – и манную, и рисовую кашу. Сколько детей любит рисовую кашу?
20. В подготовительной группе детского сада 12 человек умеют читать, 13 – считать, 7 – читать и считать. Сколько человек в группе?
Задание 3: Формализовать высказывание:
21. «Если мистер Джонс счастлив, то миссис Джонс несчастлива, и если мистер Джонс несчастлив, то миссис Джонс счастлива».
22. «Если в Варшаву мы не поедем и в горы мы не отправимся, то ежедневно будем ходить на пляж или будем читать книги».
23. «Если «Спартак» проиграет, а «Торпедо» выиграет, то «Локомотив» потеряет первое место и на третье место выйдет «Зенит»».
24. «Если я поздно приду на остановку и не смогу сесть в автобус, то опоздаю на занятия и пропущу интересную лекцию».
25. «Если завтра будет воскресенье или в институте не будет занятий, то ко мне придут друзья и мы послушаем музыку».
26. «После обеда я отправлюсь на прогулку в парк или, если ко мне зайдет приятель, то я буду играть с ним в шахматы или мы посмотрим кино».
27. «Четырехугольник является параллелограммом тогда и только тогда, когда его диагонали пересекаются и в точке пересечения делятся пополам».
28. «Если в контрольной работе я выполнил первое и третье задания, то у меня есть шанс получить положительную отметку тогда и только тогда, когда я выполню второе задание».
29. «Если в пятницу не будет дождя или снега, то мы пойдем гулять или пойдем в кино».
30. «Две прямые параллельны тогда и только тогда, когда накрест лежащие углы равны или внутренние односторонние углы равны».
Задание 4: Проверить, равносильны ли формулы:
31. 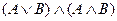 и
и 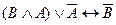 .
.
32.  и
и 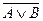 .
.
33.  и
и 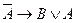 .
.
34.  и
и 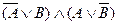 .
.
35. 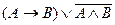 и
и 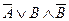 .
.
36.  и
и  .
.
37. 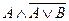 и
и 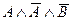 .
.
38.  и
и 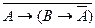 .
.
39.  и
и  .
.
40. 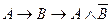 и
и 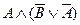 .
.
Задание 5: Решить задачу:
41. Первого сентября на первом курсе одного из факультетов запланировано по расписанию 3 лекции по разным предметам. Всего на первом курсе изучается 10 предметов. Сколько существует способов составить расписание на 1 сентября, если порядок предметов важен и если – не важен?
42. Сколькими способами можно из 15 солдат и 4 офицеров назначить в патруль трех солдат и одного офицера?
43. В некотором классе изучают 10 различных предметов. В пятницу завуч должен поставить 5 различных предметов. Сколькими способами он может это сделать, если порядок предметов важен и если – не важен?
44. В розыгрыше первенства по волейболу участвуют 12 команд. Сколько должно быть сыграно игр, если любые две команды должны сыграть между собой только один матч? Как изменится результат, если команды будут играть по 2 матча?
45. Сколько существует всего семизначных телефонных номеров, в каждом из которых ни одна цифра не повторяется; повторяется?
46. Из имеющихся семи роз и пяти веток зелени нужно составить букет, состоящий из трех роз и двух веток зелени. Сколькими способами можно составить такой букет?
47. В помещении 16 ламп. Сколько может быть различных вариантов освещения помещения, при котором должно гореть 12 ламп?
48. В вазе находятся разных по размерам 5 яблок и 6 апельсинов. Сколькими способами можно вынуть из вазы 2 яблока и 3 апельсина?
49. Каждый избиратель может занести в свой бюллетень либо одного, либо двух из 6 выдвигающихся на выборы кандидатов. Сколькими способами могут быть заполнены бюллетени?
50. Сколькими способами можно назначить патруль из двух солдат и одного офицера, если в роте имеются 80 солдат и 5 офицеров?
Задание 6: Решить задачу.
51. В ящике лежат 5 белых, 10 черных и 15 красных шаров. Какова вероятность того, что два наудачу вынутых шара будут белыми?
52. В пачке 12 билетов денежно-вещевой лотереи, 15 билетов лотереи РОСТО и 20 билетов художественной лотереи. Какова вероятность того, что наудачу вынутые два билета будут билетами денежно-вещевой лотереи?
53. В цехе работают 10 мужчин и 3 женщины. По табельным номерам наудачу выбраны 2 человека. Какова вероятность того, что выбранные люди окажутся мужчинами?
54. В цехе работают 10 мужчин и 3 женщины. По табельным номерам наудачу выбраны 2 человека. Какова вероятность того, что выбранные люди окажутся женщинами?
55. В цехе работают 10 мужчин и 3 женщины. По табельным номерам наудачу выбраны 2 человека. Какова вероятность того, что выбраны мужчина и женщина?
56. Студент, идя на экзамен, знал ответы на 70 вопросов из 90. Какова вероятность того, что студент ответит верно на предложенные ему экзаменатором 2 вопроса?
57. Школьник, идя на зачет, знал 15 из 20 предложенных к зачету вопросов. Какова вероятность того, что ему на зачете достанутся три известных ему вопроса?
58. В урне находятся 4 белых и 7 черных шаров. Какова вероятность того, что наудачу вынутые два шара окажутся белыми?
59. Из коробки, в которой имеется 4 желтых, 4 синих и 6 красных карандашей наудачу берут три карандаша. Какова вероятность того, что все карандаши синие?
60. В читальном зале есть 12 учебников по теории вероятностей, среди которых 4 новых. Наудачу берем 2 учебника. Найти вероятность того, что оба учебника новые.
Задание 7: Для данной выборки построить статистическое распределение выборки; построить полигон и гистограмму частот; дать характеристику распределения признака, вычислив для этого: 1) размах выборки; 2) медиану; 3) моду; 4) дисперсию; 5) математическое ожидание.
61. Для проведения демографических исследований выбрали 50 семей и получили следующие данные о количестве членов семьи: 2, 5, 3, 4, 1, 3, 6, 2, 4, 3, 4, 1, 3, 5, 2, 3, 4, 4, 3, 3, 2, 5, 3, 4, 4, 3, 3, 4, 4, 3, 2, 5, 3, 1, 4, 3, 4, 2, 6, 3, 2, 3, 1, 6, 4, 3, 3, 2, 1, 7.
62. Имеются следующие данные о размерах основных фондов 50 предприятий (в млн. руб.): 0,42; 0,24; 0,49; 0,45; 0,27; 0,42; 0,42; 0,5; 0,5; 0,5; 0,27; 0,25; 0,25; 0,49; 0,5; 0,42; 0,42; 0,49; 0,42; 0,24; 0,45; 0,42; 0,24; 0,49; 0,45; 0,27; 0,42; 0,5; 0,5; 0,42.; 0,42; 0,5; 0,27; 0,5; 0,49; 0,24; 0,27; 0,5; 0,45; 0,24; 0, 5; 0,42; 0,49; 0,25; 0,24; 0,3; 0,3; 0,5; 0,49; 0,42.
63. Известны данные о посевных площадях картофеля (тыс. гектаров) по районам Курганской области: 1,5; 1,5; 0,5; 1,2; 0,9; 0,9; 0,8; 0,5; 1,2; 1,1; 0,6; 1,1; 1,2; 0,9; 1,5; 1,2; 0,8; 0,4; 1,0; 0,1; 1,1; 0,8; 0,1; 1,5; 0,5; 1,2; 0,8; 0,3; 0,4; 1,3; 0,7; 0,1; 0,3; 1,6; 0,8; 0,7; 1,2; 1,5; 0,9; 0,6; 0,4, 1,0; 0,1; 1,0; 1,5; 1,2; 0,5; 1,3; 0,6; 0,8.
64. При сверлении отверстий одним и тем же сверлом и последующем измерении диаметров, получены следующие данные (в мм): 40,25; 40,35; 40,45; 40,35; 40,37; 40,35; 40,44; 40,35; 40,33; 40,41; 40,35; 40,30; 40,28; 40,30; 40,40; 40,36; 40,29; 40,33; 40,31; 40,33; 40,41; 40,40; 40,33; 40,37; 40,35; 40,34; 40,32; 40,34; 40,28; 40,46; 40,39; 40,37; 40,29; 40,39; 40,37; 40,44; 40,27; 40,38; 40,30; 40,32; 40,25; 40,36; 40,35; 40, 36; 40,33; 40,31; 40,29; 40,35; 40, 41; 40,30.
65. Имеются данные о величине латентного периода (в сек.) механического ответа при даче светового сигнала в первом предъявлении: 0,35; 0,54; 0,33; 0,33; 0,36; 0,61; 0,23; 0,25; 0,48; 0,28; 0,57; 0,29; 0,29; 0,41; 0,35; 0,36; 0,51; 0,74; 0,35; 0,44; 0,29; 0,36; 0,34; 0,34; 0,38; 0,31; 0,33; 0,32; 0,37; 0,30; 0,36; 0,35; 0,37; 0,35; 0,40; 0,37; 0,39; 0,39; 0,53; 0,45; 0,28; 0,34; 0,23; 0,44; 0,29; 0,35; 0,30; 0,37; 0,41; 0,28.
66. Имеются данные о размерах резервных фондов (в млн. руб.) 50 предприятий: 0,42; 0,24; 0,49; 0,47; 0,42; 0,24; 0,49; 0,24; 0,49; 0,40; 0,28; 0,72; 0,42; 0,47; 1,21; 0,42; 0,47; 0,48; 1,21; 0,48; 0,49; 0,72; 0,46; 0,28; 0,46; 1,21; 0,46; 1,21; 0,72; 0,49; 0,43; 0,24; 0, 47; 0,42; 1,21; 0,72; 0,88; 0,88; 1,21; 0,24; 0,28; 0, 49; 0,46; 0,24; 0,72; 0,43; 0,42; 0,47; 0,43; 0,46.
67. Имеются данные измерения длины плеча (в мм) мухоловки пеструшки на 5-й день жизни: 13,7; 14,3; 10,3; 13,0; 13,0; 12,0; 17,3; 13,0; 12,3; 10,4; 14,0; 11,3; 16,3; 11,7; 13,0; 10,4; 15,0; 14,1; 13,1; 16,3; 11,6; 11,5; 13,2; 14,3; 13,5; 10,4; 12,3; 11,3; 11,0; 13,1; 13,7; 13,1; 11,7; 13,0; 10,4; 15,0; 14,3; 11,6; 13,2; 12,0; 14,3; 11,3; 14,3; 11,6; 12,0; 16,3; 10,4; 15,0; 13,2; 11,7.
68. Имеются данные измерения величин интенсивности порогового раздражения глаз при длительности дачи света в 0,002 сек: 0,76; 2,37; 2,37; 3,14; 4,45; 4,71; 4,81; 4,81; 5,08; 5,08; 6,27; 1,29; 1,29; 1,29; 1,64; 1,56; 1,56; 1,64; 1,29; 1,56; 1,64; 1,64; 2,20; 2,11; 2,11; 2,11; 2,20; 3,14; 4,71; 4,45; 4,45; 3,28; 3,28; 3,14; 2,37; 2,20; 2,11; 2,20; 2,37; 2,37; 2,20; 3,20; 3,20; 3,11; 3,14; 3,28; 2,11; 2,37; 3,14; 2,37.
69. Имеются данные наблюдения за числом посетителей сайта университета в течение 50 дней: 70, 75, 100, 120, 75, 60, 100, 120, 70, 60, 65, 100, 65, 100, 70, 75, 60, 100, 100, 120, 70, 75, 70, 120, 65, 70, 75, 70, 100, 100, 120, 120, 100, 75, 75, 70, 70, 100, 100, 75; 75; 100; 120; 65; 100; 75; 75; 60; 120; 70.
70. Имеются данные результатов тестирования 50 студентов по математике (ответы на 50 вопросов программы): 33, 42, 27, 33, 23, 26, 31, 43, 45, 44, 16, 36, 19, 19, 23, 43, 49, 25, 22, 23, 28, 36, 36, 28, 43, 45, 21, 48, 49, 44; 15; 31; 45; 43; 44; 16; 23; 43; 25; 48; 28; 36; 44; 43; 22; 22; 16; 33; 31; 16.
Образец решения контрольной работы
Вариант 0
Задание 1: Даны множества: А и В. Найти: 1) А∩В; 2) АUВ; 3) А\В; 4) (АUВ)\(А∩В).
Решение.
А = {3, 2, 5, 7, 8, 11}, B = {1, 2, 3, 4, 5}. В соответствии с определениями операций над множествами найдем их пересечение, объединение, разность и разность множеств, являющихся их объединением и пересечением:
1) А∩В = {3, 2, 5}. Так как в пересечение множеств включаются только общие элементы.
2) АUВ = {3, 2, 5, 7, 8, 11, 1, 4}. Так как в объединение входят все элементы множеств, встречающиеся хотя бы один раз.
3) А\В = {7, 8, 11}. Так как в разность входят те элементы первого множества, которых нет во втором.
4) (АUВ)\(А∩В) = {7, 8, 11, 1, 4}.
Задание 2: Решить задачу, используя формулу Грассмана:
Из 40 учащихся класса 32 выписывают газету, 21 – журнал, 15 учащихся – и газету и журнал. Сколько учащихся не выписывают ни газету, ни журнал?
Решение.
Переведем задачу на язык множеств и изобразим ситуацию с помощью диаграмм Эйлера-Венна. Обозначим через Е множество всех учеников класса, через А – множество выписывающих газету и через В – множество выписывающих журнал.
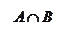
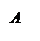


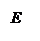
 Тогда |E| = 40, |A| = 32, |B| = 21, | AÇB| = 15. Требуется найти, чему равно |E\(AÈB)| (закрашено желтым цветом).Сначала найдем, чему равно | AÈB|, подставив известные значения в формулу Грассмана: | AÈB| = |А| + |B| - | AÇB| = 32 + 21 – 15 = 38. Теперь
Тогда |E| = 40, |A| = 32, |B| = 21, | AÇB| = 15. Требуется найти, чему равно |E\(AÈB)| (закрашено желтым цветом).Сначала найдем, чему равно | AÈB|, подставив известные значения в формулу Грассмана: | AÈB| = |А| + |B| - | AÇB| = 32 + 21 – 15 = 38. Теперь 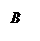 найдем |E\(AÈB)|. |E\(AÈB)| =|E| - | AÈB| = 40 – 38 = 2. Таким образом, 2 ученика не выписывают ни газету, ни журнал.
найдем |E\(AÈB)|. |E\(AÈB)| =|E| - | AÈB| = 40 – 38 = 2. Таким образом, 2 ученика не выписывают ни газету, ни журнал.
Задание 3: Формализовать высказывание: Е = «Лошадь погибает от одного грамма никотина, но я не лошадь, следовательно, курить вредно».
Решение.
Переформулируем высказывание так, чтобы все логические связки оказались в явном виде: Если лошадь погибает от одного грамма никотина и я не лошадь, то курить вредно.
Обозначим через А: «лошадь погибает от одного грамма никотина»; через В: «я не лошадь»; через С: «курить вредно». Прочитаем теперь будущую формулу, не используя текстовые высказывания: Если А и В, то С. Теперь заменим логические связки соответствующими символами логических операций: 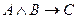 . Полученная формула является искомой.
. Полученная формула является искомой.
Задание 4: Проверить, равносильны ли формулы: G =  ; H =
; H = 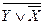 .
.
Решение.
Для проверки построим для каждой формулы таблицу истинности и сравним результаты в итоговых столбцах.
Для формулы G =  :
:
| Х | Y | 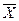
| 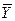
| 
|
Для формулы H = 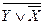 :
:
| Х | Y | 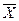
| 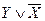
| 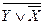
|
Так как в соответствующих строках (то есть при соответствующих наборах значений переменных) в итоговых столбцах стоят разные значения, то формулы неравносильны.
Задание 5: Решить задачу: По списку в 9 классе 15 девочек и 13 мальчиков. Нужно выбрать двух дежурных по классу. Сколькими способами это можно сделать:
а) при условии, что пару обязательно должны составить мальчик и девочка;
б) без указанного условия?
Решение.
а) Так как пару должны обязательно составить мальчик и девочка, то при составлении пары мы выбираем одного мальчика из 13 и одну девочку из 15. При этом порядок выбора не важен. Можем воспользоваться формулой сочетаний или использовать правило умножения: 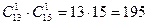 . То есть всего 195 пар, которые будут состоять из одного мальчика и одной девочки.
. То есть всего 195 пар, которые будут состоять из одного мальчика и одной девочки.
б) Теперь пара составляется без учета первого условия, то есть мы выбираем любых двух человек из 28 и порядок при этом не важен. Поэтому воспользуемся формулой сочетаний:
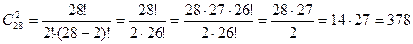 . Ответ: всего 378 пар.
. Ответ: всего 378 пар.
Задание 6: Решить задачу: В коробке «Ассорти» – 20 неразличимых по виду конфет, из которых 12 с шоколадной начинкой и 8 с фруктовой начинкой. Тане разрешили взять две конфеты. Какова вероятность того, что конфеты – с фруктовой начинкой?
Решение.
Задачу можно решить двумя способами (при решении контрольной работы нужно выбрать только один из них).
1 способ: Испытание состоит в том, что мы вынимаем 2 конфеты из коробки. Случайное событие А состоит в том, что обе конфеты с фруктовой начинкой. Общее число равновозможных исходов п – это число всех пар, которые мы можем составить из конфет, лежащих в коробке. Так как порядок конфет в парах не важен, то воспользуемся формулой сочетаний:  . Количество исходов, благоприятствующих наступлению события А (тА) – это число всех пар, которые можно составить из конфет с фруктовой начинкой. Снова воспользуемся формулой сочетаний и получим, что тА = 28. Тогда вероятность наступления события А находится по формуле:
. Количество исходов, благоприятствующих наступлению события А (тА) – это число всех пар, которые можно составить из конфет с фруктовой начинкой. Снова воспользуемся формулой сочетаний и получим, что тА = 28. Тогда вероятность наступления события А находится по формуле: 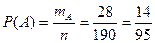 .
.
2 способ: Испытание состоит в том, что мы берем конфеты по одной (по очереди). Разделим событие А на два: А1 – первой вынута конфета с фруктовой начинкой и А2 – второй вынута конфета с фруктовой начинкой. Тогда наступление второго события зависит от наступления первого. Можно воспользоваться теоремой об условной вероятности. Так как нам надо найти вероятность одновременного появления двух событий, наступление одного из которых зависит от наступления другого, то формула для нахождения вероятности имеет вид:  . Найдем значение каждого из множителей. Так как мы выбираем одну конфету, то п = 20, а тА1 = 8. Тогда
. Найдем значение каждого из множителей. Так как мы выбираем одну конфету, то п = 20, а тА1 = 8. Тогда  . Вероятность второго события находим, учитывая, что событие А1 уже произошло: п = 19, а тА2 = 7. Тогда
. Вероятность второго события находим, учитывая, что событие А1 уже произошло: п = 19, а тА2 = 7. Тогда  . Находим искомую вероятность:
. Находим искомую вероятность: 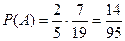 . Получили тот же ответ, что и при решении задачи первым способом.
. Получили тот же ответ, что и при решении задачи первым способом.
Задание 7: Для данной выборки построить статистическое распределение выборки; построить полигон и гистограмму частот; дать характеристику распределения признака, вычислив для этого: а) размах выборки; б) медиану; в) моду; г) дисперсию; д) математическое ожидание.
Имеются данные результатов контрольного теста по математике студентов специальности ФКиС (из 100 баллов): 15, 20, 6, 6, 24, 20, 16, 13, 13, 10, 9, 6, 19, 22, 3, 6, 6, 10, 6, 13, 21, 3, 3, 11, 3, 17, 3, 6, 3, 3, 26, 36, 15, 14, 9, 27, 19, 16, 20, 9.
Решение.
Дана выборка объема 40 (столько перечислено вариант). Запишем сначала вариационный ряд: 3, 6, 9, 10, 11, 13, 14, 15, 16, 17, 19, 20, 21, 22, 24, 26, 27, 36. Составим таблицу распределения вариант:
| Варианта, хi | Кратность варианты | Частота варианты, рi | Частота (%) варианты | хi – М(Х) |
| 0,175 | 17,5 | -9,825 | ||
| 0,175 | 17,5 | -6,825 | ||
| 0,075 | 7,5 | -3,825 | ||
| 0,05 | -2,825 | |||
| 0,025 | 2,5 | -1,825 | ||
| 0,075 | 7,5 | 0,175 | ||
| 0,025 | 2,5 | 1,175 | ||
| 0,05 | 2,175 | |||
| 0,05 | 3,175 | |||
| 0,025 | 2,5 | 4,175 | ||
| 0,05 | 6,175 | |||
| 0,075 | 7,5 | 7,175 | ||
| 0,025 | 2,5 | 8,175 | ||
| 0,025 | 2,5 | 9,175 | ||
| 0,025 | 2,5 | 11,175 | ||
| 0,025 | 2,5 | 13,175 | ||
| 0,025 | 2,5 | 14,175 | ||
| 0,025 | 2,5 | 23,175 |
Размах выборки – это разница между наибольшей и наименьшей вариантой: 36 – 3 = 33.
Медиана – это варианта, которая находится «посередине» выборки или среднее арифметическое значение «серединных» вариант. Так как вариационный ряд состоит из 18 элементов, то медианой выборки будет число, равное среднему арифметическому чисел 16 и 17: 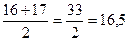 .
.
Мода – это варианта, которая встречается чаще всех. В нашей выборке таких вариант две: 3 и 6, то есть наша выборка – бимодальная.
Для вычисления математического ожидания воспользуемся формулой:  .
.
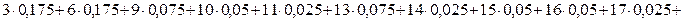
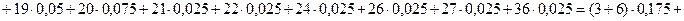
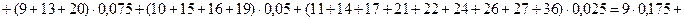
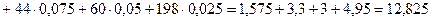 .
.
Тогда М(Х) = 12,825.
Для вычисления дисперсии, то есть величины рассеяния случайной величины Х, воспользуемся формулой: 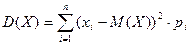 . Сначала добавим в таблицу еще один столбец, в котором запишем результаты вычисления разности хi – М(Х), а затем подставим найденные значения в формулу дисперсии:
. Сначала добавим в таблицу еще один столбец, в котором запишем результаты вычисления разности хi – М(Х), а затем подставим найденные значения в формулу дисперсии:
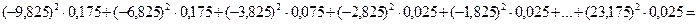 = 63,291875» 63,29.
= 63,291875» 63,29.
Осталось нарисовать полигон (многоугольник) и гистограмму частот.
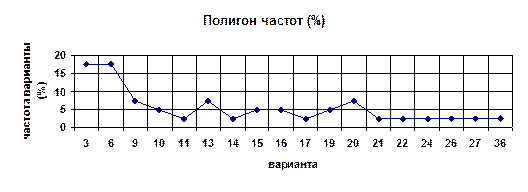
Для того, чтобы изобразить гистограмму частот, разобьем вариационный ряд на три части: [1; 12], [13; 24] и [25; 36] (интервальный ряд данных). Для каждой из этих частей найдем сумму всех кратностей и процентную частоту промежутка. Получим таблицу:
| Варианта | [1; 12] | [13; 24] | [13; 24] |
| Кратность варианты | |||
| Частота (%) | 42,5 | 7,5 |
Тогда гистограмма (столбчатая диаграмма) будет иметь вид:

ЛИТЕРАТУРА
1. Ван-дер-Варден Б.Л. Пробуждающаяся наука. Математика Древнего Египта, Вавилона и Греции. М., 1959.
2. Гаврилова О.А. Математические методы и модели в социально-правовом исследовании – М., Наука, 1980г.
3. Грес П.В. Математика для гуманитариев. Учебное пособие. – М.: Логос, 2003.
4. Даан-Дальмедико А., Пейффер Ж. Пути и лабиринты. Очерки по истории математики. М., 1986.
5. Клейн Ф. Лекции о развитии математики в XIX столетии. М., 1989.
6. Математические модели природы и общества / Калиткин Н.Н., Карпенко Н.В., Михайлов А.П., Тишкин В.Ф., Черненков М.В. - М.: ФИЗМАТЛИТ, 2005. - 360 с.
7. Мордкович А.Г., Семенов П.В. События. Вероятности. Статистическая обработка данных: Доп. параграфы к курсу алгебры 7-9 кл. общеобразоват. учреждений. – 3-е изд. – М.: Мнемозина, 2005.
8. Никольская И.Л. Знакомство с математической логикой. – М.: Московский психолого-социальный институт: Флинта, 1998.
9. Погорелов А.В. Геометрия: Учеб. для 7-11 кл. общеобразоват. учреждений. – М.: 1998.
10. Скворцова М. Математическое моделирование// Математика – приложение к газете «Первое сентября» – 2003. - № 14 – С. 1-4.
11. Шелобаев С.И. Математические методы и модели. – ЮНИТИ – 2001, 367 с.
12. Шикин Е, Шикина Г. Гуманитариям о математике. Рассказ третий. Модели// Математика – приложение к газете «Первое сентября» – 1999. - № 43 – С. 19-25.
13. Юшкевич А.П. История математики в средние века. М., 1961.
14. http://olddesign.isu.ru/~slava/do/disc/arithmet.htm
15. http://gatchina3000.ru/great-soviet-encyclopedia/bse/007/395.htm
16. http://neuronet.alo.ru/phenomenon/chapter12.htm#12.09
17. http://promo.ntv.ru/gordon/archive/12510/
18. http://gabro.ge/biblio/0707/3066/filosof.historic.ru/books/item/f00/s00/z0000616/index.htm
19. http://www.monax.ru
20. http://refhist.ru/history/mathematical_methods_and_models_in_legal_research/m/28386/1.1.html
21. http://ardis.hi-edu.ru/e-books/xbook081/01/index.html?part-003.htm#i321
22. http://readall.ru/lib_page_readall_109323.html
СОДЕРЖАНИЕ
| Введение ………………………………………………………… | |
| Памятка студенту ………………………………………………. | |
| Тема 1: Аксиоматический метод ………………………………. | |
| Тема 2: Элементы теории множеств …………………………… | |
| Тема 3: Элементы математической логики …………………… | |
| Тема 4: Элементы комбинаторики …………………………….. | |
| Тема 5: Элементы теории вероятностей ………………………. | |
| Тема 6: Элементы математической статистики ………………. | |
| Тема 7: Элементы математического моделирования ………… | |
| Тема 8: Элементы истории математики ………………………. | |
| Задачи для самостоятельного решения ……………………….. | |
| Темы рефератов ………………………………………………… | |
| Задания исследовательского характера ………………………. | |
| Вопросы к экзамену (зачету) …………………………………... | |
| Контрольная работа для студентов заочного отделения …….. | |
| Литература ……………………………………………………… |
|
|
|
|
|
Дата добавления: 2014-11-16; Просмотров: 1941; Нарушение авторских прав?; Мы поможем в написании вашей работы!