
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Системы счисления. Система счисления (С.С.) -это способ наименования и изображения чисел с помощью символов, имеющих определенные количественные значения
|
|
|
|
Система счисления (С.С.) -это способ наименования и изображения чисел с помощью символов, имеющих определенные количественные значения. В зависимости от способа изображения чисел С.С. бывают позиционные и непозиционные. В непозиционной С.С. символы, обозначающие то или иное количество, не меняют своего значения в зависимости от места в изображении количество. Примером непозиционной С.С. может служить римская, в которой для каждого числа используется специфическое сочетание символов (XIV, CXXVII и т.п.). В позиционной С.С. количественное значение каждой цифры зависит от ее места (позиции) в числе. Количество (Р) различных цифр, используемых для изображения числа в позиционной С.С., называется основанием С.С. Значения цифр лежат в пределах от 0 до Р-1. В общем случае запись любого смешанного числа в С.С. с основанием Р будет представлять собой ряд вида:
a 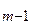 Р
Р 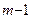 + a
+ a 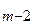 Р
Р 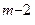 +...+ a
+...+ a 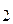 Р
Р 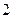 + a
+ a 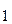 Р
Р 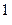 + a
+ a 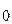 Р
Р 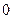 + a
+ a  Р
Р 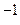 + a
+ a 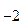 Р
Р 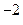 +.... + +a
+.... + +a 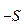 Р
Р 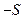 , (1)
, (1)
где нижние индексы определяют местоположение цифры в числе (разряд):
· положительные значения индексов - для целой части числа (m разрядов),
· отрицательны значения - для дробной (s разрядов).
Так, например, в общепринятой десятичной сс в последовательности цифр 777,77 одна и та же цифра 7 представляет сотни, десятки, единицы, десятые и сотые доли единицы:
777,77 = 7 * 100 + 7 * 10 + 7 *1 + 7 * 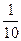 + 7 *
+ 7 * 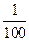 =
=
= 7 * 10 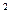 +7 *10
+7 *10 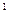 + + 7 *10
+ + 7 *10 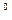 + 7 * 10
+ 7 * 10 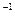 + 7 *10
+ 7 *10 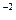 .
.
Максимальное число, которое может быть представлено в m разрядах:
N  = Р
= Р 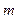 - 1.
- 1.
Минимальное значащее число (не равное 0), которое может быть представлено в s разрядах дробной части:
N 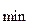 = Р
= Р 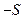 .
.
Имея в целой части m числа, а в дробной S разрядов, можно записать всего Р 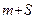 разрядных чисел.
разрядных чисел.
Двоичная С.С. имеет основание Р=2 и использует для представления информации всего две цифры: 0 и 1. Существуют правила перевода чисел из одной С.С. в другую, основанные в том числе и на соотношении (1 ). Например:
101110,101 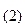 =1*2
=1*2 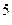 +0*2
+0*2 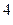 +1*2
+1*2 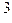 +1*2
+1*2 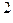 +1*2
+1*2 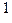 +0*2
+0*2 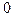 +1*2
+1*2 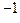 +0*2
+0*2 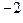 +1*2
+1*2 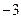 = 46,625
= 46,625 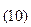 .
.
Восьмеричная С.с. имеет основание Р=8 и имеет алфавит, состоящий из цифр 0...7.
257 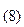 = 2*8
= 2*8 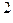 + 2*8
+ 2*8 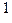 + 2*8
+ 2*8 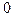 = 175
= 175 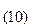 .
.
В шестнадцатеричной С.с. (Р=16) используются цифры 0...9 и латинские буквы А...F (A- соответствует 10, B-11, C-12,D-13, E-14,F-15).
AF 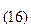 =10*16
=10*16 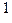 + F*16
+ F*16 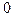 = 175
= 175 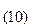 .
.
Вопросы перевода из одной С.С. в другую играют весьма важную роль для программистов, использующих языки программирования низкого уровня (микропрограммные, машинные, ассемблеры и др.). Рассмотрим некоторые приемы перевода чисел из одной С.С. в другую. Пусть имеются две С.С. с основаниями р и d. Любое целое число в этих С.С. можно представить соответственно в виде:
N 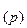 =
= 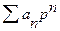 и N
и N 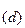 =
= 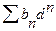 , где n = 1, 2, 3....
, где n = 1, 2, 3....
Алгоритм перевода целого числа из одной С.С. в другую состоит в следующем. На первом шаге делим в С.С. с р - основанием число N 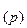 на d - основание: N
на d - основание: N 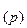 / d = N
/ d = N 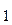
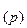 + a
+ a 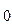 ; на втором шаге делим число N
; на втором шаге делим число N 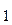
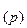 на d - основание: N
на d - основание: N 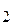
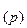 / d = N
/ d = N 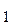
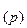 + a
+ a 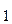 и т.д. Последний результат деления будет: N
и т.д. Последний результат деления будет: N 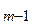
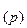 / d = N
/ d = N 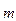
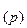 + a
+ a 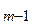 . Тогда нетрудно заметить, что число N
. Тогда нетрудно заметить, что число N 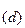 должно иметь вид:
должно иметь вид:
N 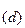 = N
= N 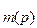 d
d 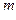 + a
+ a 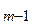 d
d 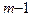 +... + a
+... + a 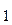 d
d 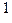 + a
+ a 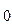 d
d 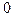 .
.
Рассмотрим теперь перевод чисел, меньших 1. В этом случае числа N 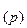 и N
и N 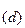 имеют следующий вид: N
имеют следующий вид: N 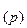 =
= 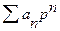 и N
и N 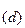 =
= 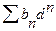 , где n = -1,-2,-3.....
, где n = -1,-2,-3.....
Алгоритм перевода дробного числа из одной С.С. в другую состоит в следующем. Hа первом шаге умножаем в С.С. с р - основанием число N 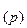 на d - основание:
на d - основание:
N 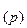 *d = b
*d = b  . N
. N 
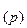 ; на втором шаге умножаем число N
; на втором шаге умножаем число N 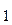
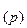 на d - основание: N
на d - основание: N 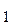
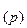 *d = b
*d = b 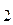 . N
. N 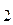
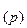 и т.д. Следует отметить, что результатом такого умножения будет последовательность цифр b
и т.д. Следует отметить, что результатом такого умножения будет последовательность цифр b 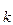 . Тогда нетрудно заметить, что число N
. Тогда нетрудно заметить, что число N 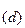 должно иметь вид: N
должно иметь вид: N 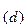 = 0. b
= 0. b 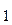 d
d 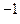 + b
+ b 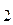 d
d 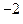 + b
+ b 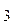 d
d 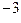 +....
+....
Для перевода смешанных чисел следует отдельно переводить их целые и дробные части согласно алгоритмам. Рассмотрим пример: 10 ® 8


 1942 8
1942 8

 16 242 8
16 242 8



 34 240 30 8
34 240 30 8




 32 2 24 3
32 2 24 3
 22 6
22 6
 16
16
6
| 0.55 | 0.40 | 0.20 | 0.60 | 0.80 | 0.40 |
 * 8 * 8
| * 8 | * 8 | * 8 | * 8 | * 8 |
| 4. 40 | 3. 20 | 1. 60 | 4. 80 | 6. 40 | 3. 20 |
В процессе умножения обнаружен период, равный (3146) 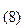 . Таким образом, результат перевода равен: 1942,55
. Таким образом, результат перевода равен: 1942,55 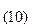 = 3626,4 (3146)
= 3626,4 (3146) 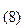 .
.
Переход от записи чисел в двоичной С.С. к восьмеричной или шестнадцатеричной и обратно осуществляется по еще более простым правилам.
Для перехода 2 ® 8 (или 16)необходимо, двигаясь справа налево, разбить двоичное число на группы по три (четыре) разряда соответственно, дополняя при необходимости левую крайнюю группу нулями. Затем каждую группу из трех (четырех) разрядов заменить соответствующей восьмеричной (шестнадцатеричной) цифрой.
Для перевода восьмеричного (шестнадцатеричного) числа в двоичное достаточно заменить каждую цифру указанного числа соответствующим трехразрядным (четырехразрядным) двоичным числом. При этом ненужные слева нули отбрасываются.
В общем случае верно утверждение: если имеются две С.С. с Р 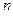 и Р
и Р 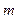 - основаниями (n = md; где m, d - целые числа), то для перевода любого числа, заданного в Р
- основаниями (n = md; где m, d - целые числа), то для перевода любого числа, заданного в Р 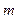 - С.С., в Р
- С.С., в Р 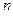 - С.С. достаточно каждую его цифру заменить Р
- С.С. достаточно каждую его цифру заменить Р 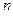 ®Р
®Р  кодом.
кодом.
В качестве примеров докажем, что 010101111 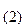 = 257
= 257 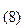 , 10101111
, 10101111 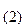 =AF
=AF 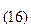 .
.






 0 1 0 1 0 1 1 1 1
0 1 0 1 0 1 1 1 1 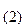 1 0 1 0 1 1 1 1
1 0 1 0 1 1 1 1 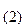
2 5 7 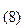 А F
А F 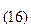


 Верны и обратные переводы: 257
Верны и обратные переводы: 257 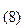 = 0 1 0 1 0 1 1 1 1
= 0 1 0 1 0 1 1 1 1 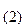 ,
,

 AF
AF 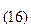 =1010 1111
=1010 1111  . 2 5 7
. 2 5 7
А F
Важность 8- и 16- С.С. в качестве промежуточных между двоичной и десятичной заключается в том, что каждый байт вмещает две шестнадцатеричные цифры, а ЭВМ работает с числами в двоичной С.С., кроме десятичной арифметики. Переводы же 16®2 и 2®16 можно делать посредством кодирования. Аналогично обстоит дело и с восьмеричной С.С.. Современная вычислительная техника использует, в основном, двоичную С.С. для хранения команд и информации, при выполнении арифметических и логических операций; С.С. с основаниями 8 и 16 используются для более компактной записи команд и содержимого памяти, а также при некоторых специфических форматах представления чисел.
|
|
|
|
|
Дата добавления: 2014-11-16; Просмотров: 1175; Нарушение авторских прав?; Мы поможем в написании вашей работы!