
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Теория реального ветряка
|
|
|
|
Работа элементарных лопастей ветроколеса. Первое уравнение связи
Выделим из лопастей ветроколеса двумя концентрическими окружностями с радиусами r и r + dr кольцевую поверхность dF = 2 πrdr. Это кольцо на крыльях вырежет отрезки длиною dr, которые называются элементарными лопастями (рис. 4.10). Через все точки обеих окружностей проведем линии тока, образующие две поверхности ABC, A ′ B ′ C ′ бутылеобразной формы (рис. 4.11). Жидкость, заключённую между этими поверхностями, назовём элементарной кольцевой струёй.
Сделаем предположение, обычно принимаемое в аналогичных теориях, что разность давлений по обе стороны ветрового колеса, действующая на площадь кольца, получающегося от пересечения ометаемой плоскостью элементарной струи, воспринимается элементарными лопастями.


Рис. 4.10. Выделение элементарных лопастей на ветроколесе.
На основании этого составляем первое уравнение связи:
2 πrdr (p 1 − p 2) = i (dY cos β + dX sin β), (1)
где Y – подъемная сила крыла, направленная перпендикулярно потоку;
X –сила сопротивления крыла(лобовое сопротивление крыла),направленная по потоку;
β –угол между плоскостью вращения ветроколеса и направлением воздушного потока, набегающего на крыло; i –число лопастей ветроколеса.

Рис. 4.11. Элементарная кольцевая струя.
Для определения направления сил, действующих на элементарную лопасть, изобразим ее сечение на рисунке 4.12, где ось Z направлена по оси ветроколеса и ось x − x в плоскости его вращения; V – направление скорости ветра; W – направление скорости относительного потока, набегающего на элемент лопасти.
Разложим силу dR, действующую на элементарную лопасть, на две силы: dX, действующую по потоку, и dY, направленную перпендикулярно потоку. Сила dX вызывает сопротивление элемента крыла; dY вызывает окружное усилие элемента крыла и называется подъёмной силой.
Вследствие вращения ветроколеса в плоскости x − x воздушный поток набегает на ветроколесо не со скоростью ветра V, а с относительной скоростью W, которая слагается геометрически из скорости ветра V и окружной скорости ωr, где ω угловая скорость и r – расстояние элемента лопасти от оси вращения ветроколеса.
Скорость потока, набегающего на элемент лопасти, в относительном движении будет равна:
 (2)
(2)

 где V 1 = V − v 1 – скорость ветра в плоскости ветряка.
где V 1 = V − v 1 – скорость ветра в плоскости ветряка.
Рис. 4.12. План скоростей воздушного потока при набегании его на элемент лопасти.
Скорость u 1 получается как реакция от крутящего момента, развиваемого лопастями. Эта скорость имеет направление, обратное моменту; её величина берётся как средняя для всей зоны, в которой работают лопасти. В действительности эта скорость перед ветроколесом равна нулю и непосредственно за ветряком равна u 2. Так как закон изменения этой скорости неизвестен, то, как первое приближение, её принимают равной:
 (3)
(3)
Силы dY и dX можно выразить как:
 , (4)
, (4)
 (5)
(5)
где b – ширина элемента лопасти по хорде.
Кроме того, на основании уравнения для лобового давления на ветряк (по теории идеального ветряка Г.Х. Сабинина) можем написать:
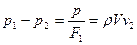 (6)
(6)
Подставляя вместо dY и dX и p 1 − p 2 их значения в уравнение (1) получим
 (7)
(7)
после сокращения получим:
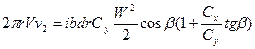 (7а)
(7а)
Или
 (7б)
(7б)
На основании рис. 4.12 можно ввести обозначение
 (8)
(8)
которое называют числом относительных модулей. Из уравнения (8) имеем:
− ωr − u 1 = − zu (V − v 1), (8а)
или
(− ωr − u 1) 2 = zu 2 (V − v 1)2, (8б)
и, зная, что V 1 = V − v 1, уравнение (2) можем переписать так:
 (9)
(9)
Заменим
 (10)
(10)
 (11)
(11)
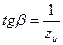 (12)
(12)
 - обратное качество крыла (13)
- обратное качество крыла (13)
и подставим их в уравнение (7б)
 . (7в)
. (7в)
Вводя в это уравнение e =  и заменив v 2 его значением из равенства
и заменив v 2 его значением из равенства  , получим:
, получим:
 (14)
(14)
Это уравнение называется уравнением связи; оно связывает ширину лопасти и коэффициент подъемной силы с деформацией потока, характеризуемой величиной e.
Взяв сумму проекций сил элемента лопасти на касательную к окружности, по которой он движется, получим окружное усилие, развиваемое элементарными лопастями:

Подставляя сюда значение W, sin β и cos β и вводя Cx = µC y, получим:
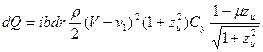 (15)
(15)
Подставляя сюда значение ibCy из уравнения (14) и сделав сокращения, получим:

 (16)
(16)
Момент относительно оси ветряка равен:
 (17)
(17)
Секундная работа элементарных лопастей:
 (18)
(18)
Секундная энергия далеко перед ветряком, заключенная в потоке, площадь сечения которого определяется площадью кольца, сметаемого элементарными лопастями, равна:
 . (18а)
. (18а)
Поделив секундную работу элементарных лопастей на эту энергию, получим элементарный коэффициент использования энергии ветра:
 . (19)
. (19)
Умножив и разделив выражение (19) на (1 − e) получим:
 . (19а)
. (19а)
Так как выражение  представляет идеальный коэффициент использования энергии ветра, то можем записать:
представляет идеальный коэффициент использования энергии ветра, то можем записать:
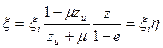 , (20)
, (20)
Где
 (21)
(21)
называют относительным коэффициентом полезного действия элементарного ветряка.
При большом числе модулей можно приблизительно считать:

И тогда
 (21а)
(21а)
Напомним, что числом модулей, или быстроходностью ветродвигателя, называют отношение окружной скорости конца лопасти к скорости ветра:
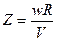 .
.
Число модулей элементов лопастей на радиусе r равно:
 . (22)
. (22)
Число модулей для любого радиуса r ветряка с известной быстроходностью Z может быть выражено так:
 , (23)
, (23)
где R – радиус ветроколеса.
Второе уравнение связи
Момент относительно оси ветряка аэродинамических сил, действующих на элементарные лопасти, равен по величине и противоположен по знаку моменту количества движения, получаемого элементарной струёй, увлечённой ветряным колесом. Здесь предполагается, что в этом процессе принимает участие и присоединённая масса, так как в противном случае теорема Гельмгольца о сохранении вихря не была бы выполнена.
Второе уравнение связи выводим из рис. 4.13.
i (dY sin β − dX cos β) r = d (m 1+ m 2)2 u 1 r (24)
но
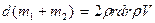 .
.
Подставляя указанное уравнение и значения dY и dX из уравнений (4) и (5) в уравнение (24), получим:
 . (24а)
. (24а)
Заменив в этом уравнении sin β и cos β их значениями из уравнений (10) и (11) и сделав сокращения, получим:
 . (24б)
. (24б)
Подставляя сюда (13) и (9), получим
 . (24в)
. (24в)
Из этого равенства находим отношение  , для чего разделим правую и левую части на 8 πrV 2 и заменим отношение
, для чего разделим правую и левую части на 8 πrV 2 и заменим отношение  его значением e
его значением e
 (25)
(25)
Подставляя их уравнения (14) значение  и проведя сокращения, получим:
и проведя сокращения, получим:
 (26)
(26)
Преобразуя уравнение (8), находим соотношение между zu и z:
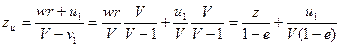 .
.
Подставим значение  из уравнения (24):
из уравнения (24):
 (27)
(27)
 (28)
(28)
Решаем это уравнение относительно  :
:
 ;
;
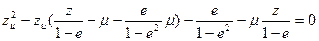 ;
;
 (29)
(29)
Так как µ обычно имеет малую величину, то, приняв µ = 0, уравнения (28) и (29) можно упростить:
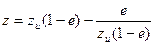 . (28а)
. (28а)
 . (29а)
. (29а)
Уравнения (14), (22) и (29) позволяют сделать полный аэро-динамический расчёт ветроколеса для заданных ωR и V, а также формы профиля крыла. При этом пользуются диаграммой C y и Cx, построенной для данного профиля.
Задаваясь e в пределах 0,28 до 0,35 и наиболее выгодным углом атаки, по диаграмме C y и Cx для данного профиля находят: µ = 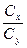 .
.
Подставляя значения z, e и µ в уравнение (29), находят число относительных модулей zu. Далее, пользуясь уравнением (14), находят суммарную ширину лопастей ib:
 . (30)
. (30)
И, наконец, определяют угол заклинения лопасти φ на радиусе r:
 . (31)
. (31)
Cy находят по диаграмме Cy по  ,построенной на основании экспериментальных данных.
,построенной на основании экспериментальных данных.
Момент и мощность всего ветряка
Момент всего ветряка получим, проинтегрировав уравнение (27) в пределах от r 0 до R, где r 0 – расстояние от оси ветряка до начала лопасти и R –расстояние от оси ветряка до конца лопасти.
 (32)
(32)
Этот момент обычно выражают в отвлеченных величинах и обозначают через  с чертой вверху. При этом правую и левую части равенства (32) делят на
с чертой вверху. При этом правую и левую части равенства (32) делят на  и вводят обозначение
и вводят обозначение  , называемую относительным радиусом:
, называемую относительным радиусом:
 (33)
(33)
Уравнение (33) является основным для вычисления характеристики моментов. Им можно пользоваться при переменных значениях e вдоль r, если предположить, что элементарные струи не влияют друг на друга, что практически допустимо при плавных изменениях e.
Для ветряка с постоянным e по радиусу мы можем вынести e за знак интеграла:
 (34)
(34)
Этот интеграл можно решить, если пренебречь кручением струи, которое у быстроходных ветряков незначительно.
Следовательно, мы можем принять u 1 = 0 и относительное число модулей zu из уравнения (8) можем выразить так:
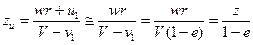 (35)
(35)
Для конца лопасти имеем:
 (36)
(36)
Разделив уравнение (35) на (36), получим
 ; (37)
; (37)
 (38)
(38)
Сделав ряд преобразований уравнения (34) и пренебрегая малыми величинами  и
и 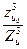 , получим:
, получим:
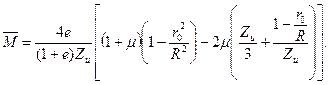 (39)
(39)
Подставляя значение  из уравнения (35), получим:
из уравнения (35), получим:
 (40)
(40)
Мощность, развиваемая ветряком, равна Mω, а так как из уравнения (33) момент равен:
 (33а)
(33а)
то мощность, развиваемую ветряком, можно написать так:
 , (41)
, (41)
Поставив сюда  вместо
вместо  , получим:
, получим:
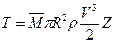 , (42)
, (42)
Заменив  его значением из уравнения (40), получим:
его значением из уравнения (40), получим:
 (43)
(43)
Разделив мощность ветряка на секундную энергию потока, получим коэффициент использования энергии ветра:
 (44)
(44)
Так как:
 и
и 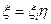
То
 (45)
(45)
При выводе этого уравнения не были приняты во внимание потери, происходящие вследствие образования вихрей, сходящих с концов лопастей, а также принято кручение уходящей струи равным нулю, что допустимо у быстроходных ветряков.
Следовательно, коэффициент использования энергии ветра, подсчитанный по формуле (44), будет значительно выше возможного к получению в практике.
Потери ветряных двигателей
Потери ветряных двигателей разделяются на четыре группы.
1. Концевые потери, происходящие за счёт образования вихрей, сходящих с концов лопастей. Эти потери определяются на основании теории индуктивного сопротивления. Часть этих потерь была учтена при выводе идеального коэффициента использования энергии ветра ξi; неучтенная часть концевых потерь выражается формулой (46):
 (46)
(46)
2. Профильные потери, которые вызываются трением струй воздуха о поверхность крыла и зависят только от профиля лопастей.
Мощность, поглощаемая профильным сопротивлением элементарных лопастей длиною dr, на радиусе r ветряка равна:
 , (47)
, (47)
где Cp – коэффициент профильного сопротивления, который для крыла бесконечного размаха равен Cx, т.е.:
Cp = Cx.
Так как  , или
, или  , то
, то  . Подставляя значение Сз, равное
. Подставляя значение Сз, равное  и
и 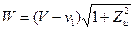 в уравнение (47), получим
в уравнение (47), получим
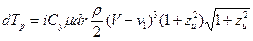 .
.
Подставляем значение  из уравнения (14) и делаем преобразования этого уравнения:
из уравнения (14) и делаем преобразования этого уравнения:

Подставляем:
 ;
;
 ;
;
 ;
;
и отбрасываем в знаменателе μ, как малую величину, по сравнению с  :
:

Интегрируя в пределах от 0 до  получим:
получим:
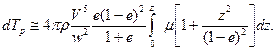
Профильные потери там, где уже кончилась лопасть, существуют в виде сопротивления маха, каковое, таким образом, учитывается приблизительно. В результате интегрирования получаем профильные потери всего ветряка:
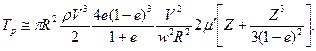
Где  есть средняя величина по всей лопасти.
есть средняя величина по всей лопасти.
Так как  и
и  , то подставляя значения этих выражений в данное уравнение и разделив его на
, то подставляя значения этих выражений в данное уравнение и разделив его на  , получим окончательную формулу профильных потерь в безразмерном значении:
, получим окончательную формулу профильных потерь в безразмерном значении:
 (48)
(48)
3. Потери на кручение струи за ветряком равны живой силе тангенциальных скоростей уходящей струи. Величину этих потерь получим, проинтегрировав живую силу от тангенциальных скоростей всех элементарных струй в пределах от r 0 до R, а именно:
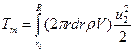 (49)
(49)
Заменим в данном выражении u 2 его значением, которое равно 2 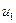 . Так на основании уравнений (25) и (21)
. Так на основании уравнений (25) и (21)

 и
и  ,
,
Получим

Следовательно:

Откуда:

Или
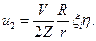 (50)
(50)
Подставляя значение 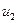 в уравнение (49), получим:
в уравнение (49), получим:
 .
.
Вынося постоянные за знак интеграла и заменив η некоторым его значением η 1, средним для всего радиуса r, получим:
 .
.
Поделив обе части этого равенства на мощность идеального ветряка:
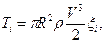
получим отвлечённую величину потерь на кручение струи за ветряком:
 (51)
(51)
4. Потери, происходящие вследствие неполного использования всей ометаемой площади, учитываются отношением:

Полезную мощность, развиваемую ветряком, получим, вычтя все потери из мощности идеального ветряка:
 .
.
Разделив на Ti получим:

Откуда:
 (52)
(52)
Разделив правую и левую части этого уравнения на выражение энергии ветра  , получим коэффициент использования энергии ветра реального ветряка:
, получим коэффициент использования энергии ветра реального ветряка:
 (53)
(53)
Так как, согласно уравнению (20), 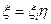 , находим, что относительный коэффициент полезного действия
, находим, что относительный коэффициент полезного действия  ветряка равен:
ветряка равен:
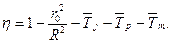 (54)
(54)
|
|
|
|
|
Дата добавления: 2014-11-08; Просмотров: 2542; Нарушение авторских прав?; Мы поможем в написании вашей работы!