Изображение проекций точек при различном их положении в пространстве

Прямоугольные проекции и координаты точек. Эпюр (чертеж) Г.Монжа

Предмет, задачи и метод начертательной геометрии

Изображение точки, прямой, плоскости и простейших геометрических поверхностей в ортогональных проекциях

Лекция 1. Предмет, задачи и метод начертательной геометрии

· Эпюр (чертеж) Г.Монжа. Изображение проекций точек при различном их положении в пространстве.

· Изображение прямой линии в ортогональных проекциях. Прямые общего и частного положения.

· Определение натуральной величины отрезка и углов наклона прямой к плоскостям проекций.

· Взаимное положение прямых. Понятие конкурирующих точек. (самостоятельно)

· Задание плоскости в ортогональных проекциях.

· Прямые и точки в плоскости.

· Главные линии плоскости.

· Плоскости частного положения.

Начертательная геометрия это наука изучающая методы изображения реальных пространственных объектив – зданий, сооружений, деталей машин – состоящих из совокупности точек, линий, поверхностей и методы решения геометрических задач по данным изображениям. Вместе с этим решается и очень существенная задача – развитие пространственного воображения.

Метод начертательной геометрии – метод проекций. Так как любой предмет можно рассматривать как совокупность множества точек, то сущность метода проецирования рассмотрим на примере точки.

Для построения проекции точки, зададим плоскость П₁ – плоскость проекций и точку А – оригинал (любая точка пространства). Проведем через точку А проецирующий луч (АА¹) до пересечения с плоскостью П₁ в точке А¹. Точка А¹ и является проекцией точки А на плоскость П₁ (рисунок 1.1). Если проецирующий луч АА¹ перпендикулярен плоскости проекций П₁, то проецирование называется прямоугольным, а точка А¹ называется прямоугольной или ортогональной проекцией точки А.

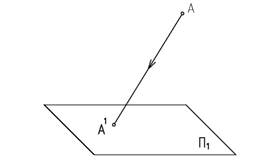
На рисунке 1.1 видно, что одна проекция точки не определяет ее положения в пространстве, так как в точку А¹ проецируются все точки проецирующего луча АА¹. Для того чтобы положение точки в пространстве было определено, возьмем три взаимно перпендикулярные плоскости П₁, П₂, П₃ (рисунок 1.2).

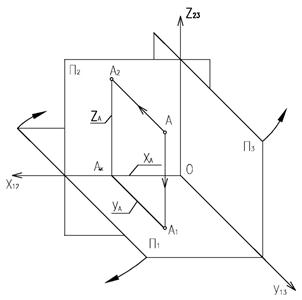П₁ – горизонтальная плоскость проекции;

П₂ – фронтальная плоскость проекций;

П₃ – профильная плоскость проекций.

Плоскости проекций пересекаясь дают оси проекций – x₁₂; y₁₃; z₂₃.

Спроецируем ортогонально точку А на эти плоскости проекций. Получим соответственно:

А₁ - горизонтальная проекция точки А;

А₂ - фронтальная проекция точки А;

А₃ – профильная проекция точки А.

В трехмерном пространстве положение точки определяется тремя (декартовыми) координатами А (x_А; y_А; z_А). Совместив декартовую систему координат с осями проекций, получим начало координат – точку О. Ось ОХ совместим с осью x₁₂, ось ОY – с осью y₁₃, ось ОZ – с осью z₂₃. Горизонтальная плоскость проекции П₁ совместится с координатной плоскостью OXY, П₂ º XOZ, П₃ º YOZ. Тогда точка А и ее проекции определяться координатами:

А (x_А; y_А; z_А) Û А₁ (x_А; y_А); А₂ (x_А; z_А); А₃ (y_А; z_А);

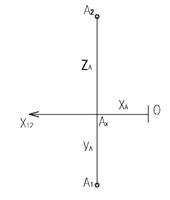По чертежу видно, что две проекции точки полностью определяют положение точки в пространстве, так как содержат все три координаты.

Для перехода от пространственного чертежа к плоскому, плоскость П₁ повернем вокруг оси х₁₂ до совмещения с плоскостью П₂. При этом звенья ломаной А_ХА₁ и А_ХА₂ образуют прямую А₁А₂ перпендикулярную оси x₁₂. Линия А₁А₂ называется линией связи проекций А₁ и А₂.

Плоский чертеж состоящий из горизонтальной А₁ и фронтальной А₂ проекций точки А, расположенных на линии связи А₁А₂ перпендикулярной оси x₁₂ называется эпюром (ортогональным чертежом) и носит имя основателя начертательной геометрии Г.Монжа (рисунок 1.3).

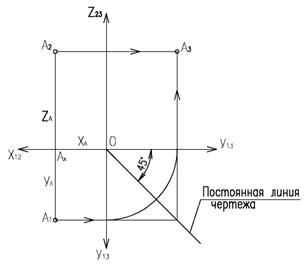Иногда возникает необходимость по двум проекциям построить третью. На рисунке 1.4 показано построение профильной проекции А₃ по двум заданным горизонтальной А₁ и фронтальной А₂ с помощью постоянной линии чертежа k₁₂₃.

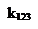Плоскости П₁ и П₂ делят все пространство на четыре четверти, отмеченные на рисунке 1.5 римскими цифрами I, II, III и IV.

Точки могут находиться в любой четверти, лежать на плоскостях проекций или на осях.

Необходимо освоить две задачи.

Первая – по паре проекций точек находящихся на плоскостях проекций определить положение точки в пространстве.

Вторая – по положению точки в пространстве изобразить ее парой проекций.

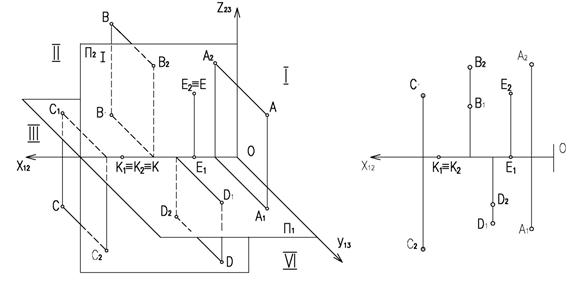
На рисунке 1.5 точка А находится в I четверти. Все ее координаты имеют положительное значение – фронтальная проекция находится над осью x₁₂, горизонтальная – под осью.

Точка В, находится во II четверти. Ее координата y_В – отрицательна – обе проекции находится над осью.

У точки С, находящейся в III четверти отрицательными будут координаты y_С и z_С. Фронтальная проекция находится под осью x₁₂, горизонтальная – над осью.

У точки D, находящейся в IV четверти, отрицательная координата z_D – обе проекции находится под осью x₁₂.

У точки Е, находящейся на плоскости П₂, координата y_Е = 0, откуда следует, что ее горизонтальная проекция Е₁ лежит на оси x₁₂ (если точка лежит на какой-то плоскости проекций, то одна из ее проекций обязательно лежит на оси).

Точка К лежит на оси x₁₂, координаты x_К и y_К равны нулю, а проекции К₁ и К₂ совпадают (К₁ º К₂).

Дата добавления: 2014-11-16