Мода и медиана. Среднее квадратическое отклонение

Среднее квадратическое отклонение

Роль математического ожидания и дисперсии на практике

Пример 1: Если нужно сравнить две марки стали по уровню ударной вязкости, что достаточно для каждой марки стали вычислить математическое ожидание ударной вязкости. Лучшей будет та марка стали, у которой математическое ожидание окажется выше

Пример 2: При одинаковом значении математического ожидания более качественным является стальной лист, имеющий минимальный разброс механических свойств. Тот лист лучше, у которого меньше значение дисперсии, т.е. меньше разброс механических свойств.

Для оценки рассеяния возможных значений случайной величины вокруг ее среднего значения кроме дисперсии служат и некоторые другие характеристики. К их числу относятся среднее квадратическое отклонение, определяемое по формуле:

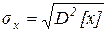Дисперсия квадрата совпадает с размерностью х - средним квадратическим отклонением.

Определение: Модой дискретной случайной величины называется ее наиболее вероятное значение.

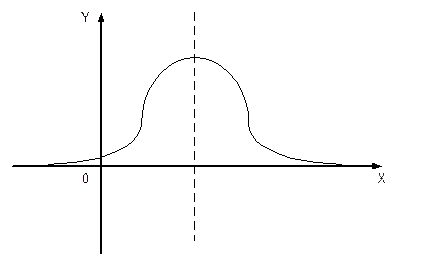Геометрически мода является абсциссой в точке кривой распределения или полигона распределения. Ордината которой max-на. В общем случае мода и математическое ожидание не совпадают.

Модой непрерывной случайной величины называется то ее значение, при котором плотность распределения f(x) – максимальна. В частном случае, когда распределение является симметричным и имеет моду, и существует математическое ожидание; то оно совпадает с модой и с центром симметрии распределения.

Медианой непрерывной случайной величины называется такое ее значение, для которого одинаково вероятно окажется ли случайная величина меньше либо больше медианы.

.

Геометрически медиана – абсцисса точки, в которой площадь ограниченной кривой распределения делится пополам. В случае симметричного распределения, имеющего моду, медиана совпадает с математическим ожиданием и модой.

Дата добавления: 2014-11-16