
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Условные вероятности. Независимость событий
|
|
|
|
В ряде случав приходится рассматривать вероятности событий при условии, что имело место некоторое другое событие. Такие вероятности называются условными и обозначаются Р(А / В).
Пример. Брошены две игральные кости.Чему равна вероятность того,что сумма выпавших очков равна 8, если известно, что эта сумма является четным числом?
Пусть А – сумма выпавших очков равна 8,
В – сумма выпавших очков четное число.
Найдем сначала безусловную вероятность Р(А) по классическому определению. Число всех возможных исходов эксперимента n =6 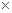 6=36, а сумма очков, равная 8, выпадет в следующих комбинациях:
6=36, а сумма очков, равная 8, выпадет в следующих комбинациях:
(2,6), (3,5), (4,4), (5,3), (6,2).
Таким образом m =5 и Р(А) = 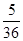 .
.
Теперь вычислим вероятность события А при условии, что наступило событие В. В этом случае возможные исходы эксперимента составляют комбинации, при которых сумма выпавших очков- четное число, таких комбинаций – 18, поэтому m = 5, n = 18, а условная вероятность Р(А / В) = 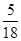 .
.
Два события А и В называются независимыми, если наступление одного из них не влияет на вероятность наступления другого, иными словами, если условная вероятность равна безусловной, Р(А / В) = Р(А). В противном случае события считают зависимыми. Так, в приведенном выше примере, события А и В являются зависимыми.
События А  ,А
,А 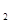 , …, А
, …, А 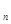 называются независимыми в совокупности, если для любого А
называются независимыми в совокупности, если для любого А  из их числа и любого подмножества данной совокупности, событие А
из их числа и любого подмножества данной совокупности, событие А  и произведение событий из подмножества взаимно независимы.
и произведение событий из подмножества взаимно независимы.
Рассмотрим пример. Тетраэдр,три грани которого окрашены соответственно в красный, зеленый и синий цвета, а четвертая грань содержит все три цвета, бросается наудачу на плоскость. События А, В, С состоят в том, что тетраэдр упал на грань, содержащую соответственно красный, зеленый либо синий цвет.
Безусловные вероятности Р(А) = Р(В) = Р(С) =  ,
,
условные вероятности Р(А/В) = Р(А/С) = Р(В/С) = Р(С/А) = Р(В/А) =  .
.
Следовательно попарно события - независимы, однако Р(А/ВС) = 1, а это свидетельствует о том,что в совокупности события - зависимы.
Рассмотрим формулы, которые используються для вычисления вероятностей сложных событий. Сложным событием называется наблюдаемое событие,
выраженное через другие наблюдаемые в том же эксперименте события с помощью допустимих алгебраических операций.
Формула сложения. Для произвольных событий А и В справедливо соотношение
Р(А+В) = Р(А) + Р(В) - Р(АВ)
Для произвольного конечного числа событий формулы сложения имеет вид:
Р(А  +А
+А 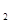 +…+А
+…+А 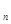 )=Р(А
)=Р(А  )+ Р (А
)+ Р (А 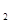 )+…+ Р(А
)+…+ Р(А 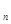 )–Р(А
)–Р(А  А
А 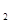 )-Р(А
)-Р(А  А
А 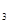 )-…- Р(А
)-…- Р(А  А
А 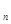 )+Р(А
)+Р(А  А
А 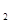 А
А 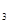 )+Р(А
)+Р(А  А
А 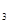 А
А 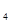 )+…+Р(А
)+…+Р(А 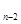 А
А  А
А 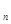 )-… (-1)
)-… (-1)  Р(А
Р(А  А
А 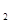 …А
…А 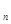 ).
).
Для несовместных событий вероятность суммы событий равна сумме вероятностей этих событий, т.е.
Р(А  +А
+А 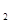 +…+А
+…+А 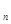 ) = Р(А
) = Р(А  )+ Р (А
)+ Р (А 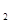 )+ … + Р(А
)+ … + Р(А 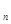 )
)
Формула умножения. Для произвольных событий А и В
Р(АВ) = Р(А) Р(B/A)=P(B)P(A/B.
Формула справедлива, если Р(А) > 0, P(B) > 0, и позволяет вычислять вероятность совместного осуществления событий А и В в тех случаях, когда условная вероятность считается известной (из дополнительных опытов) или определяется методом вспомогательного эксперимента.
Для произвольного конечного числа событий формула умножения имеет вид:
Р(А  А
А 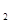 …А
…А 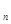 )=Р(А
)=Р(А  ) Р(А
) Р(А 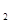 / А
/ А  )Р(А
)Р(А 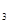 /А
/А  А
А 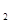 )Р(А
)Р(А 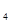 /А
/А  А
А 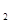 А
А 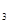 )…Р(А
)…Р(А 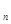 /А
/А  А
А 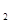 …А
…А  ).
).
Для независимых в совокупности событий вероятность произведения событий равна произведению их вероятностей, т.е.
Р(А  А
А 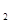 …А
…А 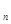 ) = Р(А
) = Р(А  А
А 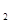 …А
…А 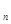 ).
).
Пример 4. В условиях эксперимента, рассмотренного в примере 3 найти вероятности того, что среди выбранных изделий содержатся:
а) не более одного бракованного;
б) хотя бы одно бракованное.
Пусть событие А - среди выбранных изделий не более одного бракованного,
Рассмотрим события: А  - среди выбранных изделий - ни одного бракованного,
- среди выбранных изделий - ни одного бракованного,
А  - среди выбранных изделий - одно бракованное.
- среди выбранных изделий - одно бракованное.
Тогда А = А  + А
+ А  , причем А
, причем А  , А
, А  - несовместны. По формуле сложения искомая вероятность Р(А) =Р(А
- несовместны. По формуле сложения искомая вероятность Р(А) =Р(А  + А
+ А  ) =Р(А
) =Р(А  ) +Р(А
) +Р(А  ),
),
Р(А  ) =
) = 
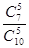 =
= 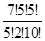 =
=  , Р(А
, Р(А  ) =
) =  =
= 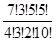 =
= 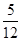 ,
,
Р(А) = 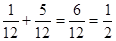
Пусть событие В – среди выбранных изделий хотя бы одно бракованное.
Можно решить эту задачу с помощью формулы сложения, но решение будет значительно проще, если перейти к противоположному событию  - среди выбранных изделий нет бракованных.
- среди выбранных изделий нет бракованных.
 = А
= А  , Р(
, Р( ) = Р (А
) = Р (А  ) =
) =  , Р(В) = 1 - Р(
, Р(В) = 1 - Р( ) = 1 -
) = 1 -  =
= 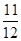
Пример 5. Определить вероятность того, что выбранное наудачу изделие является первосортным, если известно, что 5% всей продукции является браком, а 80% небракованных изделий удовлетворяют требованиям 1-го сорта.
Обозначим А – выбранное изделие является небракованным,
В – выбранное изделие удовлетворяет требованиям 1-го сорта,
тогда АВ – выбранное изделие является первосортным, а искомая вероятность
Р(АВ) = Р(А)Р(В/А) = 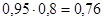 ,
,
здесь Р(А) = 1 – 0,05, Р(В/А) = 0,8.
|
|
|
|
|
Дата добавления: 2014-11-16; Просмотров: 677; Нарушение авторских прав?; Мы поможем в написании вашей работы!