Последовательность независимых испытаний. Формула Бернулли

На практике приходится сталкиваться с задачами, которые можно представить в виде многократно повторяющихся испытаний, в результате каждого из которых может появиться или не появиться событие А. При этом интерес представляет исход не каждого отдельного испытания, а общее число появлений события А в результате определенного количества испытаний. В подобных случаях нужно уметь определять вероятность любого числа m появлений события А в результате n испытаний.

Рассмотрим случай, когда испытания являются независимыми и вероятность появления события А в каждом испытании одинакова и равна р,тогда

Р() = 1 – р = q. Рассмотрим пример.

Монету подбрасывают 5 раз. Найти вероятность того, что герб появится 3 раза.

Обозначим события:

А - появление герба в одном испытании,

В - герб появится 3 раза в серии из пяти испытаний.

С помощью алгебраических действий событие В можно записать:

В = ААА + А АА + А АА + ААА + А АА + А А А +

+

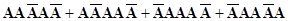
В каждое произведение событие А входит 3 раза, а событие 5-3=2 раз, число слагаемых равно .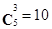

По формулам сложения и умножения получим

Р(В) = Р(ААА ) + Р(А АА ) + Р(А АА) + Р( ААА) + Р( А АА) + + Р(А А А) + Р(АА А ) + Р(А АА ) + Р( ААА ) + Р( АА А) =

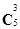
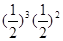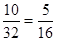= = , это и есть формула Бернулли.

Запишем эту формулу в общем виде. Пусть Р(n,m) – вероятность того, что в n

независимых испытаниях событие А наступит m раз. Тогда

Р(n,m) = .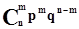

Доказательство формулы Бернулли аналогично решению рассмотренной выше задачи.

Пример 9. Изделия некоторого производства содержат 5% брака. Найти вероятность того, что среди шести, взятых наудачу изделий:

1) будут два бракованных;

2) не будет бракованных;

3) будет хотя бы одно бракованное.

Здесь А – появление бракованного изделия, Р(А) = 0,05, Р() = 1- 0,05 = 0,95,

n=6. По формуле Бернулли

1) при m = 2, Р(6,2) = 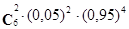= 0,03;

2) при m = 0, Р(6,0) = (0,95) 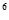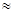0,73;

3) в этом случае задачу можно решить двумя способами.

Первый способ. Используя формулу сложения, получим

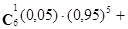
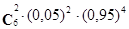
Р(6,1) + Р(6,2) = 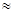0,27.

Второй способ. Перейдем к противоположному событию – среди выбранных изделий нет бракованных. Вероятность этого события вычислена в п.2) и равна 0,73. Тогда искомая вероятность

Р(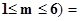 1 – 0,73 = 0,27.

Дата добавления: 2014-11-16