Математическое ожидание

Числовые характеристики случайной величины.

Лекция 7.

Случайные величины помимо законов распределения могут описываться также числовыми характеристиками.

Математическим ожиданием М (x) случайной величины называется ее среднее значение.

Математическое ожидание дискретной случайной величины вычисляется по формуле

М (x) = , (1)

где – значения случайной величины, р _i - ихвероятности.

Рассмотрим свойства математического ожидания:

1. Математическое ожидание константы равно самой константе

М (С) = С

2. Если случайную величину умножить на некоторое число k, то и математическое ожидание умножится на это же число

М (kx) = kМ (x)

3. Математическое ожидание суммы случайных величин равно сумме их математических ожиданий

М (x₁ + x₂ + … + x_n) = М (x₁) + М (x₂) +…+ М (x_n)

4. М (x₁ - x₂) = М (x₁) - М (x₂)

5. Для независимых случайных величин x₁, x₂, … x_n математическое ожидание произведения равно произведению их математических ожиданий

М (x₁, x₂, … x_n) = М (x₁) М (x₂) … М (x_n)

6. М (x - М (x)) = М (x) - М (М(x)) = М (x) - М (x) = 0

Вычислим математическое ожидание для случайной величины из Примера 11.

М (x) = = .

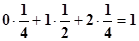Пример 12. Пусть случайные величины x₁, x₂ заданы соответственно законами распределения:

x₁ Таблица 2

а	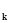- 0,1	- 0,01		0,01	0,1
р	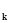0,1	0,2	0,4	0,2	0,1

x₂ Таблица 3

b	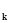- 20	- 10
р	0,3	0,1	0,2	0,1	0,3

Вычислим М (x₁) и М (x₂)

М (x₁) = (- 0,1) 0,1 + (- 0,01) 0,2 + 0 · 0,4 + 0,01 · 0,2 + 0,1 · 0,1 = 0

М (x₂) = (- 20) 0,3 + (- 10) 0,1 + 0 · 0,2 + 10 · 0,1 + 20 · 0,3 = 0

Математические ожидания обеих случайных величин одинаковы- они равны нулю. Однако характер их распределения различный. Если значения x₁ мало отличаются от своего математического ожидания, то значения x₂ в большой степени отличаются от своего математического ожидания, и вероятности таких отклонений не малы. Эти примеры показывают, что по среднему значению нельзя определить, какие отклонения от него имеют место как в меньшую, так и в большую сторону. Так при одинаковой средней величине выпадающих в двух местностях осадков за год нельзя сказать, что эти местности одинаково благоприятны для сельскохозяйственных работ. Аналогично по показателю средней заработной платы не возможно судить об удельном весе высоко- и низкооплачиваемых работниках. Поэтому, вводится числовая характеристика – дисперсия D (x), которая характеризует степень отклонения случайной величины от своего среднего значения:

D (x) = M (x - M (x))² . (2)

Дисперсия –это математическое ожидание квадрата отклонения случайной величины от математического ожидания. Для дискретной случайной величины дисперсия вычисляется по формуле:

D (x) = 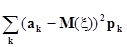= 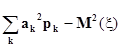(3)

Из определения дисперсии следует, что D (x) 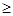0.

Свойства дисперсии:

1. Дисперсия константы равна нулю

D (C) = 0

2. Если случайную величину умножить на некоторое число k, то дисперсия умножится на квадрат этого числа

D (kx) = k² D (x)

3. D (x) = М (x²) – М² (x)

4. Для попарно независимых случайных величин x₁, x₂, … x_n дисперсия суммы равна сумме дисперсий.

D (x₁ + x₂ + … + x_n) = D (x₁) + D (x₂) +…+ D (x_n)

Вычислим дисперсию для случайной величины из Примера 11.

Математическое ожидание М (x) = 1. Поэтому по формуле (3) имеем:

D (x) = (0 – 1)²·1/4 + (1 – 1)²·1/2 + (2 – 1)²·1/4 =1·1/4 +1·1/4= 1/2

Отметим, что дисперсию вычислять проще, если воспользоваться свойством 3:

D (x) = М (x²) – М² (x).

Вычислим дисперсии для случайных величин x₁, x₂ из Примера 12 по этой формуле. Математические ожидания обеих случайных величин равны нулю.

D (x₁) = 0,01· 0,1 + 0,0001· 0,2 + 0,0001· 0,2 + 0,01· 0,1 = 0,001 + 0,00002 + 0,00002 + 0,001 = 0,00204

D (x₂) = (-20)² · 0,3 + (-10)² · 0,1 + 10² · 0,1 + 20² · 0,3 = 240 +20 = 260

Чем ближе значение дисперсии к нулю, тем меньше разброс случайной величины относительно среднего значения.

Величина 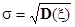называется среднеквадратическим отклонением. Модой случайной величины x дискретного типа Md называется такое значение случайной величины, которому соответствует наибольшая вероятность.

Модой случайной величины x непрерывного типа Md, называется действительное число, определяемое как точка максимума плотности распределения вероятностей f(x).

Медианой случайной величины x непрерывного типа Mn называется действительное число, удовлетворяющее уравнению

F(x) = .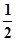

Дата добавления: 2014-11-16