Уравнение Бернулли. Трубка тока (поверхность тока)

Трубка тока (поверхность тока)

Выделим в движущейся жидкости замкнутый контур, через каждую точку которого проведем линии тока (рис.4.5).

Рис. 4.5. Трубка тока

Образованная таким образом цилиндрическая поверхность носит название трубки тока. Данный контур намечался в прост­ранстве, занятом движущейся жидкостью, поэтому часть ее должна находиться и внутри трубки тока. Количество жидкости внутри поверхности тока или трубке тока будет оставаться постоянным с течением времени, так как по определению она образована линиями тока, касательными к поверхности трубки тока и жидкость не может втекать и вытекать из нее. Данное свойство трубки тока является необходимым при определении объемного и массового расхода жидкости.

Объемным расходом принято называть объемное количество жидкости, проходящей через данное живое сечение в единицу времени, в системе СИ объемный расход измеряется в .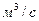

Внутри трубки тока объемный расход остается постоянный.

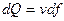(4.9)

Объемный расход жидкости через поверхность 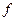реального потока будет равен

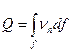(4.10)

где - проекция скорости на нормаль к площадке.

Массовым расходом называют массу жидкости, проходящей через рассматриваемое сечение в единицу времени. Массовый расход в системе СИ измеряется в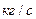

Массовый расход жидкости через поверхность 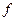равен абсолютному значению

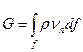(4.11)

Важной характеристикой потока или конечной струйки является

средняя скорость потока в данном сечении.

Это понятие вводится для упрощения решений многих технических расчетов и практических задач, так как в реальных потоках вязкой жидкости локальные скорости по живому сечению распределяются неравномерно.

Средней скоростью называется одинаковая для всех точек сечения фиктивная скорость, при которой данное живое сечение пропускает тот же расход, что и при действительных неравномерно-распределенных локальных скоростях.

Уравнение неразрывности или сплошности (уравнение расхода)

Уравнение неразрывности – это частный случай уравнения сохранения массы жидкости во времени для изолированной системы .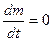

Условимся считать что жидкость, втекающая в выделенный объем в виде параллелепипеда через первую грань вдоль оси будет положительна, а вытекающая через вторую грань будет отрицательна.

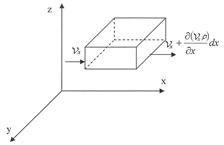
Рис. 4.6 К выводу дифференциального уравнения сплошности

Изменение массы жидкости вытекающей из второй грани вдоль оси за время 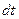из параллелепипеда составит:

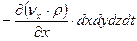(4.21)

Аналогично на все координатные оси

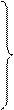
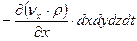
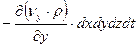(4.22)

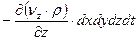
Суммарное изменение массы внутри элементарного параллелепипеда за счет разности приносимой потоком в параллелепипед и уносимой из него массы по трем координатам 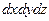и за время 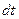составит

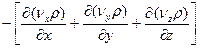(4.23)

Из математики известно, что:

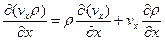
Изменение массы в неизменном объеме возможно только тогда, когда меняется плотность жидкости.

Изменение плотности по координатам с течение времени будет:

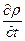
Откуда

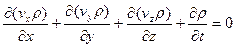(4.24)

Сгруппировав слагаемые, получим уравнение неразрывности или сплошности:

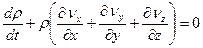(4.25)

Для несжимаемой жидкости 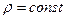, тогда расход по длине струйки тока не меняется в данный момент времени и имеет одно и тоже значение.

(4.26)

Уравнения (4.26) называются уравнениями неразрывности (расхода) в гидравлической форме для несжимаемой жидкости.

Профессор Казанского университета И.С. Громека преобразовал уравнения Эйлера в иную форму, соответствующую идеальной, несжимаемой, однородной жидкости. Массовые силы для большинства практических задач соответствовали силе тяжести. Режим движения данной жидкости был стационарным, т.е. 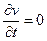и безвихревой.

Умножим каждое из уравнений Эйлера последовательно на 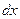, , 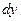и .

Система дифференциальных уравнений Л. Эйлера для идеальной движущейся жидкости на координатные оси

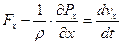
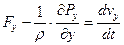
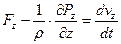
Раскроем скобки и сгруппируем, получим:

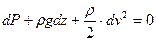(5.7)

Это выражение называют уравнением Бернулли в дифференциальной форме. При условии 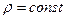(для несжимаемой жидкости) интегрирование его дает:

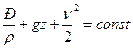, (5.8)

Этот интеграл называют интегралом Бернулли, из уравнения (5.8.) следует, что сумма удельной кинетической 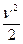, удельной потенциальной энергии и удельной работы сил давления - есть величина постоянная.

Для того, чтобы записать интеграл Бернулли в размерностях давления, умножим обе части (5.8) на плотность 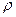и получим

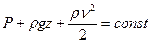(5.9)

(5.10)

где:

- удельная потенциальная энергия единицы объема жидкости, Па.

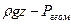геометрическое давление - удельная энергия положения единицы объема жидкости, Па.

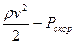скоростное давление - удельная кинематическая энергия единицы объема жидкости, Па.

Таким образом, уравнение Бернулли это частный случай закона сохранения энергии.

Дата добавления: 2014-11-16