Движение газа с высокими скоростями

При движении газовых потоков с высокими скоростями необходимо учитывать изменение плотности газа, которое сопровождается изменением температуры.

Первое начало термодинамики для движущегося потока газа учитывает изменение внутренней и внешней энергии потока. Запас внутренней энергии зависит от состояния термодинамической системы. Движущийся поток газа обладает кинетической энергией направленного движения частиц газа и их потенциальной энергией. Запишем уравнение первого начала термодинамики.

, (11.1)

где - подведенная к единицы массы газа теплота; - удельная внутренняя энергия системы; - удельная потенциальная энергия частиц движущегося газа; - удельная кинетическая энергия газа; -работа, совершаемая единицей массы газа.

При движении газа потенциальную энергию массовых сил, как правило не учитывают.

При адиабатическом движении газа (без подвода и отвода теплоты) и уравнение (11.1) запишется:

(11.2)

где ; - удельный объем системы.

Из определения энтальпии известно, что , , тогда уравнение (11.1) запишется:

; (11.3)

Уравнение (11.3) справедливо для реального и идеального газа, при адиабатном течении газа, его скорость может определяться формулой

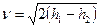
Для изобарного процесса , уравнение (11.3) запишем для двух сечений

(11.4)

Из уравнения (11.4) следует, что если газ разгоняется во втором сечении потока, тогда его температура падает.

Из уравнения Менделеева – Клапейрона известно:

где - удельная газовая постоянная,

Уравнение Майера связывает изобарную и изохорную теплоемкости:

,

где - показатель адиабаты

Уравнение (11.4) можно записать:

(11.5)

Из физики известно, что при движении газа возникают упругие колебания среды, представляющие собой малые механические возмущения в виде сжатий и разряжений. Скорость распространения этих возмущений называют скоростью распространения звука.

; ;

где 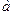- местная скорость распространения звука, .

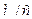Скорость распространения звука в идеальном газе зависит от абсолютной температуры и физических свойств газа и не зависит от условий движения, приняв процесс распространения звука изотермическим, получим:

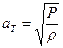(11.6)

Так как, или , то уравнение (11.5) запишем:

(11.6)

Уравнение(10.15) является еще одной формой записи уравнения Бернулли, из которого следует, что при возрастании скорости потока адиабатического газа, местная скорость звука в нем убывает, а при торможении возрастает.

Дата добавления: 2014-11-16