Метод зон Френеля. Прямолинейное распространение света

Принцип Гюйгенса-Френеля в рамках волновой теории должен был ответить на вопрос о прямолинейном распространении света. Френель решил эту за­дачу, рассмотрев взаимную интерференцию вторичных волн и применив прием, получивший название метода зон Френеля.

Рис. 16

Найдем в произвольной точке М амплитуду световой волны, распростра­няющейся в однородной среде из точечного источника S (рис. 16). Согласно принципу Гюйгенса-Френеля, заменим действие источника S действием воображаемых источников, расположенных на вспомогательной поверхности Ô, являющейся поверхностью фронта волны, идущей из S (поверхность сферы с центром S). Френель разбил волновую поверхность О на кольцевые зоны та­кого размера, чтобы расстояния

от краев зоны до М отличались на 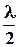, т.е. 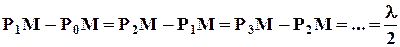. Подобное раз­биение фронта волны на зоны можно выполнить, проведя с центром в точке М сферы радиусами

,

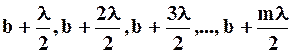Так как колебания от соседних зон проходят до точки М расстояния, отли­чающиеся на l/2, то в точку М они приходят в противоположной фазе, и при наложении эти колебания будут взаимно ослаблять друг друга. Поэтому амп­литуда результирующего светового колебания в точке М

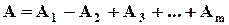(4.1)

где 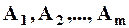- амплитуды колебаний, возбуждаемых 1-й, 2-й,..., m-й зонами. Интенсивность излучения в направлении точки М уменьшается с ростом m и вследствие увеличения расстояния от зоны до точки М. Учитывая оба этих фактора, можем записать

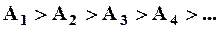
В качестве допустимого приближения можно считать, что амплитуда коле­бания А_m, от некоторой m-й зоны Френеля равна среднему арифметичес­кому от амплитуд примыкающих к ней зон, т.е.

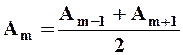. (4.2)

Тогда выражение (4.1) можно записать в виде

А = А₁/2 + (А₁/2 – А₂ + А₃/2) + (А₃/2 – А₄ +А₅/2) +…=А₁/2. (4.3)

Выражения, стоящие в скобках, согласно (4.2), равны нулю, а оставшаяся часть от амплитуды последней зоны + А _m /2 ничтожно мала.

Таким образом, амплитуда, создаваемая в произвольной точке М сфери­ческой волновой поверхностью, равна половине амплитуды, создаваемой одной центральной зоной. Следовательно, действие всей волновой поверхности на точку М сводится к действию ее малого участка, который меньше центральной зоны. Расчеты показывают, что радиус внешней границы m-й зоны Френеля

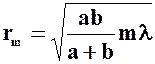. (4.4)

При a = b = 10 см и l = 0,5 мкм радиус первой (центральной) зоны r1 =0,158 мм. Следовательно, распространение света от S к М происходит так, будто световой поток распространяется внутри очень узкого канала вдоль SМ, т.е. прямолинейно. Таким образом, принцип Гюйгенса-Френеля позволяет объяснить прямолинейное распространение света в однородной среде.

Правомерность деления волнового фронта на зоны Френеля подтверждена экспериментально. Для этого используются зонные пластинки. В простейшем случае стеклянные пластинки, состоящие из системы чередующихся прозрачных и непрозрачных концентрических колец, построенных по принципу расположения зон Френеля, т.е. с радиусами r_m зон Френеля, определяемыми выражением (4.3) для данных значений а, b и l (m=0,2,4,... для прозрачных и m=1,3,5,... для непрозрачных колец). Если поместить зонную пластинку на расстоянии а от точечного источника и на расстоянии b от точки наблюдения на линии, соединяющей эти две точки, то для света дли­ной волныl она перекроет четные зоны и оставит свободными нечетные начи­ная с центральной. В итоге результирующая амплитуда 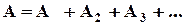должна быть больше, чем при полностью открытом фронте. И в самом деле: на опыте зонная пластинка во много раз увеличивает интенсивность света в точке М, действуя подобно собирающей линзе.

Дата добавления: 2014-11-16