Статистичні графіки

.

Ймовірність того, що помилка вибірки буде не більше заданого значення 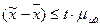являє собою функцію S (t, n) наведену в таблицях Ст'юдента в літературі з математичної статистики:

Таблиці Ст'юдента свідчать, що при збільшенні обсягу вибірки розподіл Ст'юдента наближуються до нормального закону і при n = 20 він мало відрізняється від нормального розподілу. Приклад. Визначення помилки при випадковому безповторному відборі методом малої вибірки.

На зерноприймальному пункті формуються партії зерна для подальшого його сушіння. Для встановлення режиму роботи зерносушарки необхідно знати вологість зерна, яка буде встановлена впродовж дня взяттям вибірково 10 проб з автомашин із зерном.

Номер проби
Вологість зерна, %	18,4	17,8	18,0	17,5	17,7	18,8	19,	17,9	18,6	18,7

Визначити:

1. середню вологість зерна пшениці за вибірковою сукупністю;

2. середню та граничну помилки вибіркової середньої;

3. межі, в яких з ймовірністю 0,954 перебуває середня вологість зерна у генеральній сукупності.

Зробити висновки.

Таблиця 9.4. – Розрахунок середньої вологості зерна та дисперсії малої

вибірки

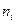
	18,4	0,16	0,026
	17,8	-0,44	0,194
	18,0	-0,24	0,058
	17,5	-0,74	0,547
	17.7	-0,54	0,292
	18,8	0,56	0,314
	19,0	0,76	0,577
	17,9	-0,34	0,115

Продовження табл. 9.4.

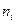
	18,6	0,36	0,130
	18,7	0,46	0,211
Разом	182,4	х	2,274

1.Середнє значення вологості зерна пшениці за даними таблиці:

.

За даними таблиці розраховуємо вибіркову дисперсію:

.

2. Середня квадратична похибка вибірки дорівнює:

.

Отже вибіркова середня = 18 24% є оцінкою генеральної середньої з середньою похибкою .

При заданому рівні ймовірності Р=0,954 коефіцієнт довіри t при малій вибірці може бути визначено з використанням математичних таблиць розподілу Ст'юдента, які є в навчальній літературі: t = 2,26 при рівні значимості - 0,05 та числі ступенів вольності К = п- 1 = 10-1 =9.

Тоді гранична похибка вибірки дорівнює

3. Встановимо інтервальну оцінку середньої вологості зерна пшениці в генеральній сукупності.

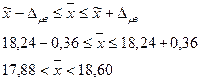
Таким чином, з ймовірністю 0,954 можна стверджувати, що середня вологість зерна в генеральній сукупності перебуває в інтервалі від 17,88% до 18,60%.

10. Графічний метод (подання статистичних даних: таблиці, графіки)

10.1. Статистичні таблиці

Результати статистичного зведення та групування оформляють у вигляді статистичних таблиць та статистичних графіків.

Статистична таблиця – це форма раціонального та наочного представлення числових даних, які характеризують досліджувані явища та процеси.

За змістом статистична таблиця являє собою закінчену думку, що подана в цифрах. Статистична таблиця – це комбінація горизонтальних рядків та вертикальних граф. Їх перетин утворює клітини таблиці. Ліві бічні, верхні клітини призначені для заголовків, а решта – для цифрових даних. Сукупність горизонтальних рядків і вертикальних граф без цифрових даних називається макетом статистичної таблиці (рис. 10.1).

Таблиця «як статистична думка» має свій підмет і присудок.

Статистичний підмет – це група або окремі одиниці сукупності, що досліджуються статистикою.

Присудком є показники, за допомогою яких характеризують об’єкт або групи досліджуваної сукупності. Підмет розміщують в лівій частині таблиці, в назвах горизонтальних рядків. Присудок в правій частині вертикальних граф.

Присудок   Підмет	Заголовки граф
А
Перелік (групи) одиниць сукупності

Рис.10.1 – Макет статистичної таблиці

Залежно від структури підмета розрізняють три види статистичних таблиць: прості, групові, комбінаційні.

Прості таблиці будуються без групувань підмета. Такі таблиці можуть бути переліковими, хронологічними, територіальними.

Груповими називають таблиці, в підметі яких містяться групування одиниць спостереження за однією ознакою.

Комбінаційні таблиці – це такі таблиці, підмет яких містить групування одиниць спостереження за декількома ознаками одночасно.

Складання статистичної таблиці здійснюється в два етапи. На першому етапі розробляється макет таблиці, на другому – макет заповнюється статистичними даними.

Результати спостереження та групування соціально-економічних явищ і процесів можуть бути представлені на графіках.

Статистичний графік – це масштабне подання статистичних даних за допомогою ліній, геометричних фігур, інших наочних засобів. Статистичні графіки відрізняються великою різноманітністю і представлені в двох групах: діаграми та статистичні карти.

Найбільш поширеною групою графіків є діаграми, які в залежності від способу побудови бувають: стовпчикові, стрічкові, фігурні, лінійні, секторні тощо.

Стовпчикові діаграми (рис. 10.2) використовуються для наочного зіставлення обсягів явища, що вивчається за часом або в просторі.

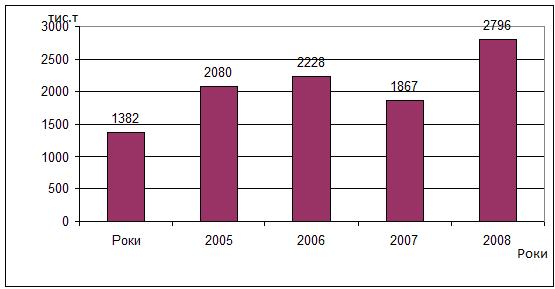
Рис.10.2 – Виробництво соняшникової олії нерафінованої, тис.т

Вертикальні стовпчики в масштабі відповідають чисельним значенням ознаки. Стовпчики можуть розміщуватися один від одного на однаковій відстані, або щільно. Їх зображення може бути площинним або об’ємним.

Якщо стовпчики розміщуються не вертикально, а горизонтально, то такі діаграми звуться с трічковими або смугастими.

За допомогою лінійних діаграм найчастіше відображають динаміку (розвиток) явищ в часі. Їх будують в масштабі у прямокутній системі координат: на осі абсцис відкладають періоди або моменти часу, на осі ординат – числові значення показника. На перетині ліній відповідних значень досліджуваної ознаки і перпендикулярів числових дат отримують точки. Ламана лінія, що їх з’єднує, характеризує зміну явища у часі.

Лінійні графіки використовують також для вивчення зв’язків між показниками (графік зв’язку). В цьому випадку на осі абсцис відкладають значення факторного показника, а на осі ординат – значення результативного показника у відповідному масштабі. Прикладом побудови лінійних графіків може бути залежність плинності робочої сили від величини середньої заробітної плати по підприємству.

Секторні діаграми (рис.10.3.) характеризують структуру явища. Для побудови секторної діаграми круг розділяється радіусами на сектори, площі яких пропорційні частинам явища в загальному обсязі круга, що дорівнює 100% або 360˚. Перед побудовою діаграми абсолютні значення величин ознаки переводять у проценти, а проценти – у градуси (1% дорівнює 3,6˚-360˚:100).

Рис.10.3 – Структура використання насіння ріпаку в Україні в 2008/2009 МР.

Розрахункові або аналітичні графіки використовуються для спрощення аналітичних розрахунків. Як приклад розглядається графік розрахунку точки беззбитковості (критичного обсягу) (рис. 10.4.

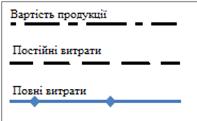
Рис.10.4 – Точка беззбитковості переробки зерна

Другою групою статистичних графіків є статистичні карти: картограми і картодіаграми.

Картограма – це зображення певної ознаки на схематичній географічній карті різними забарвленнями або штрихуванням.

Картодіаграма являє собою поєднання схематичної географічної карти з однією із згаданих вище діаграм (статистичні показники зображуються у вигляді стовпчиків, квадратів, трикутників, силуетів тощо).

При досліджуванні рядів розподілу в практиці статистики інколи використовуються графіки. Такі графіки полегшують аналіз рядів розподілу, дозволяють отримати уявлення про форму розподілу. Найчастіше при цьому використовують полігон розподілу (дискретні ряди), та гістограму (інтервальні ряди).

Полігон розподілу зображають у прямокутній системі координат, де на осі абсцис відкладають значення варіанти х, а на осі ординат – частоти f. Одержаної точки перетину з координатами 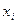і з’єднують прямими лініями (рис. 10.5).

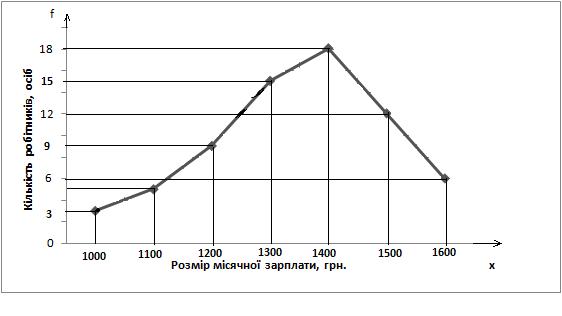
Рис.10.5 – Полігон розподілу робітників цеху за розміром заробітної плати

Гістограмою називається графік, на якому ряд розподілу зображується за допомогою суміжних один з одним стовпчиків.

Наприклад, урожайність цукрових буряків у фермерських господарствах за звітний рік характеризується такими даними.

Урожайність 100-200 ц/га мали 5 господарств

200-300 ц/га – 15 господарств

300-400 ц/га – 20 господарств

400-500 ц/га – 15 господарств

500-600 ц/га – 5 господарств

600-800 ц/га – 3 господарств

На основі цих даних побудуємо гістограму розподілу фермерських господарств за урожайністю цукрових буряків. Висота стовпчика є пропорційна частотам. Ширина стовпчика при рівних інтервалах буде рівновеликою, а при нерівних неоднаковою (рис. 10.6).

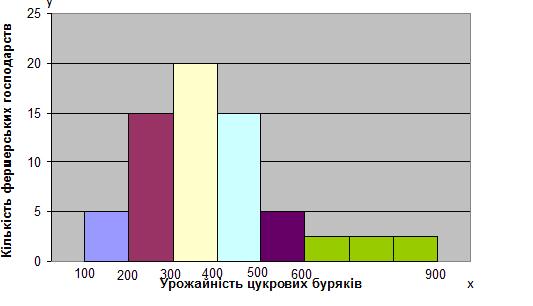
Рис.10.6 – Гістограма розподілу фермерських господарств за урожайністю цукрових буряків

В ряді випадків для зображення варіаційних рядів використовується комулянта. Для її побудова на осі абсцис відкладають варіанти х,а на осі ординат – накопичені частоти (частки) F, які розраховуються шляхом сумування частот даної групи. Зображення варіаційного ряду у вигляді комулянти зручно при зіставленні варіаційних рядів, а також в економічних дослідженнях (наприклад, для аналізу концентрації виробництва).

Зміст

Тема 1.	Методологічні засади статистики
1.1. Історія розвитку статистики
1.2. предмет статистик як науки
1.3. Положення, категорії статистичної науки
1.4. Статистична методологія
1.5. Організація національної та міжнародної статистики
Тема 2.	Статистичне спостереження
2.1. Статистичне спостереження як метод інформаційного забезпечення
2.2. Програмно-методологічне та організаційне забезпечення спостереження
2.3. Форми, види та способи спостереження
2.4. Помилки спостереження та методи їх контролю
Тема 3.	Зведення та групування статистичних даних
3.1. Суть статистичного зведення
3.2. Основні класифікації в економічній статистиці національної економіки
3.3. Групування статистичних даних
Тема 4.	Статистичні показники
	4.1. Суть і значення статистичних показників
	4.2. Абсолютні величини
	4.3. Відносні величини
	4.4. Середні величини
	4.5. Система статистичних показників
Тема 5.	Ряди розподілу
	5.1. Суть і види рядів розподілу. Елементи рядів розподілу
	5.2. Мода і медіана
	5.3. Статистичне вивчення варіації
	5.4. Обчислення дисперсії
Тема 6.	Методи аналізу взаємозв’язків
	6.1. Види взаємозв’язків
	6.2. Регресійний аналіз
	6.3. Оцінка щільності
Тема 7.	Ряди динаміки
	7.1. Суть, складові елементи та види рядів динаміки
	7.2. Характеристика динамічних рядів
	7.3. Методи обробки динамічних рядів
	7.4. Вимірювання сезонних коливань в рядах динаміки
Тема 8.	Індекси
	8.1. Суть індексів
	8.2. Методологічні принципи побудови індексів
	8.3. Індивідуальні індекси
	8.4. Агрегатна форма загальних індексів кількісних показників
	8.5. Агрегатна форма загальних індексів якісних показників
	8.6. Агрегатна форма загальних індексів змішаних показників
	8.7. Загальні індекси середніх величин
Тема 9.	Вибіркове спостереження
	9.1. Суть вибіркового спостереження
	9.2. Характеристика генеральної та вибіркової сукупності
	9.3. Похибки вибіркового спостереження
	9.4. Різновиди вибірки
	9.4.1. Проста випадкова вибірка
	9.4.2. Механічна вибірка
	9.4.3. Мала вибірка
Тема 10.	Графічний метод
	10.1. Статистичні таблиці
	10.2. Статистичні графіки

Дата добавления: 2014-11-16