На основе модульной оптимизации

Проектирование систем подчиненного регулирования

ПРОЕКТИРОВАНИЕ СИСТЕМЫ УПРАВЛЕНИЯ

Принципы модульной оптимизации. В общем случае критерий оптимальной настройки контуров подчиненного регулирования заключается в том, что регулируемая величина должна как можно точнее следовать за изменением задания, а также возможно меньше отклоняться от заданного значения при действии возмущений.

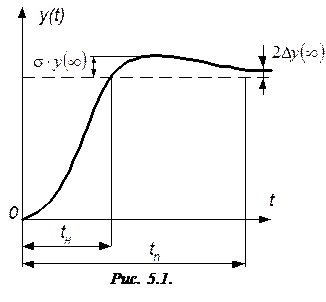Важной особенностью оптимизации контуров по модульному оптимума является строгая регламентация характера переходного процесса. Тогда критерий настройки может быть сформулирован следующим образом. Необходимо, чтобы переходная характеристика по задающему воздействию настроенного по модульному оптимуму контура удовлетворяла следующим условиям:

– перерегулирование s не должно превосходить наперед заданного значения;

– время нарастания 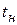и переходного процесса должно быть возможно меньше.

На рис. 5.1 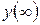– установившееся значение контролируемой величины, а 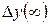– допустимая ошибка управления.

При получении расчетных зависимостей выгоднее перейти к частотным характеристикам. Тогда критерий оптимизации для замкнутых систем сформулируем следующим образом. Амплитудная частотная характеристика замкнутого контура должна удовлетворять следующим условиям:

– модуль частотной характеристики должен стремиться к единице при стремлении частоты w к нулю;

– необходимо, чтобы показатель колебательности 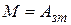превышал единицу на малое, наперед заданное значение;

– частота среза должна быть возможно больше.

Для удовлетворения второго и третьего условий, т.е. для получения как можно лучшего прилегания к горизонтали =1 и увеличения , потребуем, чтобы возможно больше производных от по w в точке w = 0 обращались в нуль.

Математически модульный оптимум формулируется следующим образом:

(5.1)

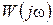– частотная характеристика разомкнутого контура. Частотная характеристика замкнутого контура имеет следующий вид:

.

Квадрат модуля частотной характеристики замкнутой системы может быть найден из соотношения

.

В выражение входит только в виде четных степеней, т.е. 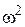, , 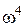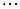. Объясняется это тем, что – вещественная функция, а w в нечетной степени возможно только в сочетании с множителем j (мнимой единицей). Следовательно, 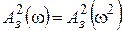. Обозначим . Если обозначить также 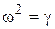, то . В этом случае условие (5.1) можно переписать в иной форме:

(5.2)

Приведенные соотношения (5.2) и представляют собой окончательную формулировку модульного оптимума.

Предположим, что объект управления не содержит интегрирующих и форсирующих звеньев, а его передаточная функция имеет вид:

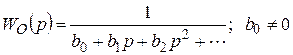. (5.3)

Для улучшения динамических свойств системы регулятор должен содержать форсирующие звенья, а для устранения статической ошибки – хотя бы одно интегрирующее звено. Передаточная функция регулятора может быть представлена при этом в следующем виде:

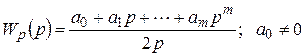. (5.4)

Как видно из приведенных передаточных функций порядок объекта не ограничен, требуется только, чтобы он не содержал форсирующих и интегрирующих звеньев. Порядок числителя регулятора ограничен, что связано с необходимостью его практической реализации. Используя условия оптимизации по модульному оптимуму, определяются коэффициенты 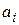передаточной функции регулятора (5.4) по известным коэффициентам передаточной функции (5.3) объекта. Решение для 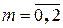приведено в таблице 5.1.

На основании таблицы 6.1 можно получить расчетные параметры основных типов регуляторов для объектов управления, представляющих собой соединение различных динамических звеньев (таблицы 5.2, 5.3 и 5.4).

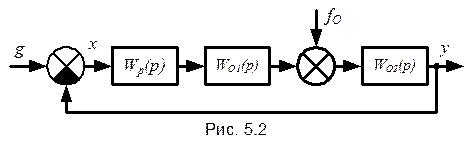В случае оптимизации по модульному оптимуму, когда объект имеет интегрирующее звено, а возмущающее воздействие 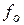приложено до этого звена, система будет обладать статической ошибкой 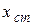(рис. 5.2). Введя обозначения: 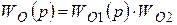– передаточная функция составного объекта; 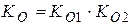– коэффициенты передачи объекта; 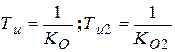– постоянные времени интегрирующего звена объекта, получим расчетные зависимости для настройки регуляторов, приведенные в таблице 5.4.

Таблица 5.1. Расчетные формулы для определения параметров регулятора

Тип регулятора, порядок его числителя	Передаточная функция регулятора	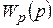Расчетные формулы
И – регулятор т = 0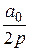
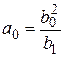
ПИ – регулятор т = 1
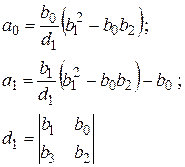
ПИД – регулятор т = 2

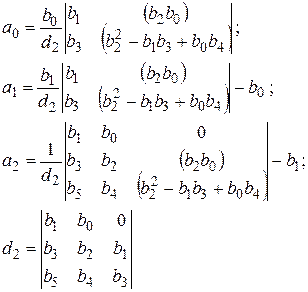
Таблица 5.2. Расчетные формулы для определения параметров регулятора для объектов, содержащих апериодические звенья

Передаточная функция объекта	Тип регулятора и его передаточная функция	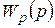Расчетная зависимость параметров регулятора от параметров объекта
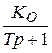
	И-регулятор
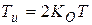
,	И-регулятор
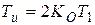
ПИ-регулятор
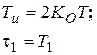
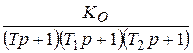
и	И-регулятор
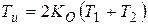
ПИ-регулятор
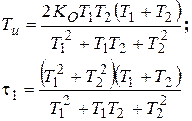
ПИД-регулятор

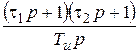
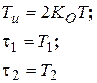
Таблица 5.3. Расчетные формулы для определения параметров регулятора для объектов, содержащих колебательное звено или звено запаздывания

Передаточная функция объекта	Тип регулятора и его передаточная функция	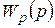Расчетная зависимость параметров регулятора от параметров объекта
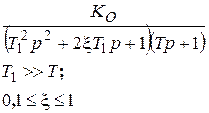
	И-регулятор
ПИ-регулятор
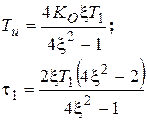
ПИД-регулятор
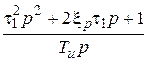
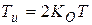
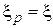
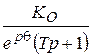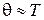
,	И-регулятор
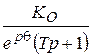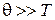
,	И-регулятор
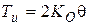
ПИ-регулятор
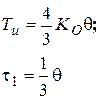
ПИД-регулятор

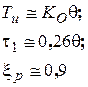
Таблица 5.4. Расчетные формулы для определения параметров регулятора для объектов, содержащих интегрирующие звенья, а также апериодические звенья с большими постоянными времени

Передаточная функция объекта	Тип регулятора и его передаточная функция	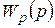Расчетная зависимость параметров регулятора от параметров объекта
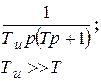
	П-регулятор
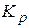
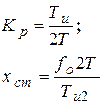
	ПД-регулятор
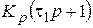
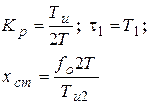
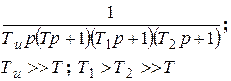
	ПД^2-регулятор
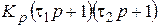
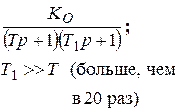
	П-регулятор
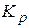
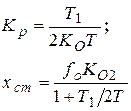
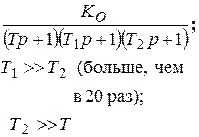
	ПД-регулятор
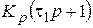
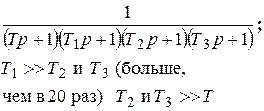
	ПД^2-регулятор

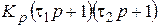
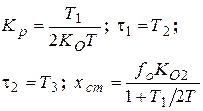
Дата добавления: 2014-11-08