Трехмерная графика

Трехмерная графика предназначена для построения на плоскости графиков функций двух переменных (двух аргументов) . Список функций, используемых в двумерной графике, может быть выведен в Command Window по команде

help graph3d.

4.1. Общие принципы построения трехмерных графиков

При построении в трехмерном пространстве графиков функций двух переменных соблюдаются следующие общие правила:

1) если z – вектор, то будем иметь один график функции z аргументов х и у;

2) если z – матрица, то будем иметь графики функций, заданных столбцами матрицы z, аргументов х и у;

3) перед построением трехмерных графиков необходимо выполнить формирование сетки на плоскости ХОУ по заданным значениям аргументов функции х и у. Сетка формируется из вспомогательных матриц Х и У по известным векторам х и у. Х – матрица, строки которой – копии вектора х, У – матрица, столбцы которой – копии вектора у. Матрицы Х и У должны иметь одинаковые размеры: число строк каждой из них должно быть равно длине вектора у, а столбцов – длине вектора х. Для формирования сетки удобнее всего использовать специальную функцию

[X, Y]=meshgrid(x,y);

Если область определения и шаг значений переменных х и у одинаковы, то допускается короткий формат

[X, Y]=meshgrid(x);

Задавая шаг сетки, следует помнить, что при построении сетчатых графиков выполняется линейная интерполяция. Ранее, при обсуждении правил построения двумерных графиков, был приведен пример последствий неверно заданного размера (большого) шага (см. рис. 4.4). Аналогичные неприятности могут возникнуть и при 3D-рисовании графиков.

4.2. Построение трехмерных графиков

Matlab предоставляет пользователю большое разнообразие функций построения трехмерных графиков (поверхностей). Основные из низ приведены в табл. 4.5. Сетчатые поверхности (каркасные графики) отображаются с автоматическим нанесением сеток. Для функций возможно применение параметров Linespec и PropertyName управления свойствами графиков (см. разд. 3.4).

Таблица 4.5

Функция	Формат использования	Назначение
plot3	plot3(x,y,z) x, y – матрицы, формирующие сетку; z – вектор или матрица значений функции в узлах сетки	Трехмерный график в виде двумерных линий
mesh	mesh(x,y,z)	Трехмерный сетчатый график
meshс	meshс(x,y,z)	Трехмерный сетчатый график с горизонталями (проекциями сечения поверхности на плоскость ХОУ)
meshz	meshz(x,y,z)	Трехмерный сетчатый график с вертикальными плоскостями ("занавесками")
surf	surf(x,y,z)	Трехмерный сетчатый график с окрашиванием поверхности
surfl	surfl(x,y,z,'light') параметр 'light' указывает на подсветку (может отсутствовать)	Трехмерный сетчатый график с окрашиванием поверхности и подсветкой
surfс	surfс(x,y,z)	Трехмерный сетчатый график с окрашиванием поверхности и горизонталями
contour3	contour3(x,y,z,n) n – количество линий уровня (может выбираться автоматически)	Трехмерный график в виде линий уровня (контурных линий)

Пример: пусть требуется построить график функции двух переменных 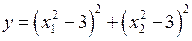для 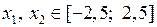. Реализуем построения в режиме прямых вычислений.

В окне Command Window выполним следующую последовательность команд:

>> [X,Y]=meshgrid(-2.5:0.1:2.5);

>> Z=(X.^2-3).^2+(Y.^2-3).^2;

>> plot3(X,Y,Z)

>> grid, title('График функции y=(х1^2-3)^2+(x2^2-3)^2')

>> xlabel('x1'), ylabel('x2')

>> zlabel('y(x1,x2)')

Результат – трехмерный график в виде двумерных линий приведен на рис. 4.8, а. На рис. 4.8, б показан график той же самой функции, построенный функцией meshc.

а б

Рис. 4.8. Использование функций трехмерной графики:

а – plot3; б – meshc

Сетчатая поверхность (рис. 4.8, б) является более информативной: ячейки сетки деформируются в соответствии с изгибами поверхности и цвет позволяет судить о значениях функции – бóльшие значения окрашены в теплые цвета (красная гамма), меньшие – в холодные (синяя гамма). Кроме того, снизу показаны проекции сечений поверхности на плоскость ХОУ. Недостатком изображений на рис. 4.8 является то, что затруднительно определить значения функции и аргументов. Выход может быть найден при помощи контурных графиков (табл. 4.6).

Например, для функции из предыдущего примера можно получить дополнительную информацию, рассчитав линии уровня и построив их на плоскости.

Таблица 4.6

Функция	Формат использования	Назначение
contour	contour(x,y,z,n)	Рисование n линий уровня (n может не задаваться)
contourf	contourf(x,y,z,n)	Рисование n линий уровня с заливкой промежутков между ними цветами, соответствующими значениям исследуемой функции
clabel	clabel(cs,h) cs – матрица с информацией о линиях уровня; h – указатели, которые можно получить как [cs, h]=contour(x,y,z)	Рисование линий уровня с указанием для каждой значения функции

>> [cs, h]=contour(X,Y,Z);

>> clabel(cs,h)

>> grid

>> title('Линии уровня функции у=(х1^2-3)^2+(х2^2-3)^2')

>> xlabel('x1'), ylabel('x2')

Результат показан на рис. 4.9 (число линий уровня определяется по умолчанию).

Рис. 4.9. Маркированные линии уровня

4.3. Управление свойствами трехмерных графиков

Помимо параметров Linespec и PropertyName, которые могут использоваться в функциях построения поверхностей, имеются специальные средства управления свойствами трехмерных графиков. Основные из них приведены в табл. 4.7.

Таблица 4.7

Средство	Формат использования	Назначение
colormap	colormap(c) c – матрица m ×3 вещественных чисел из диапазона [0; 1].	Задание палитры цветов
shading interp	shading interp	Команда замены сетчатой поверхности сплошной
colorbar	colorbar Ставится последней	Команда вывода на поле графика шкалы цветов, устанавливающей соответствие со значениями функции

Число строк в матрице с, задающей палитру цветов, может быть любым. Оно отображает число цветовых интервалов между невидимыми горизонтальными сечениями, считая их снизу от плоскости ХОУ. Каждая строка матрицы с содержит тройку элементов, формирующих палитру графика на соответствующем интервале из трех цветов – красного, зеленого и синего (так называемая RGB -палитра): черному цвету соответствует [0 0 0], белому – [1 1 1], серому – [0.5 0.5 0.5]. Удобнее выбирать одну из стандартных палитр, задавая ее имя в виде

colormap(ИмяПалитры)

Символические имена основных палитр приведены в табл. 4.8.

Таблица 4.8

Имя палитры	Палитра
autumn	Красно-желтая
bone	Серо-синяя
cool	Фиолетово-голубая
gray	Оттенки серого
hsv	Радуга
pink	Розовая
summer	Желто-зеленая
white	Белая (бесцветная)
winter	Сине-зеленая

По умолчанию установлена палитра hsv. Функция colormap может стоять как до, так и после функции построения графиков. Восстановление палитры hsv выполняется с помощью следующего обращения к функции:

colormap('default')

Дата добавления: 2014-11-08