Аппроксимация

На практике аппроксимация используется, как правило, для сглаживания данных или для определения параметров (коэффициентов) функций, общий вид которых известен. Аппроксимирующая функция обычно моделирует всю таблицу. Чаще всего для целей аппроксимации используется метод наименьших квадратов, при котором минимизируется сумма квадратов отклонений моделирующей 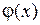и моделируемой 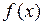функций в узлах таблицы.

2.1. Моделирование полиномом по методу

наименьших квадратов

Полиномы в Matlab представляются в виде вектора коэффициентов, расположенных в порядке УБЫВАНИЯ степеней. Число элементов в векторе (число коэффициентов полинома) всегда на единицу больше его степени. Нулевые коэффициенты должны содержаться в векторе, несмотря на то, что в записи формулы полинома они в явном виде не присутствуют. Так, например, для определения полинома 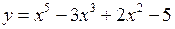необходимо задать вектор-строку из шести значений

р=[1 0 -3 2 0 5].

Полиномиальная аппроксимация данных, которые сформированы в виде вектора y, при определенных значениях аргумента, образующих вектор x такой же длины, как и вектор y, по методу наименьших квадратов осуществляется при помощи функции pоlyfit. Обращение к функции следующее:

p=pоlyfit(x,y,n)

где n – порядок аппроксимирующего полинома. Результатом является вектор р длиной n+1 из коэффициентов моделирующего полинома. По K табличным точкам можно построить полином не более чем 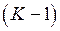-й степени.

Примечание: при работе с полиномами полезными бывают следующие функции Matlab:

v=polyval(p,x) – вычисление вектора v значений полинома, заданного вектором коэффициентов р, для аргумента, заданного векторoм х;

r=roots(p) – вычисление вектора r всех корней полинома, заданного вектором коэффициентов р;

p=ploy(r) – определение вектора коэффициентов полинома р по вектору его корней r.

Пример. Пусть некоторая неизвестная функция 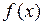задана координатами восьми ее точек (таблицей значений). Требуется моделировать 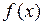полиномом 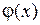(найти порядок полинома, наилучшим образом приближающего ).

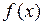Решение. Используя функцию polyfit, построим пять моделирующих полиномов порядка от 1 до 5.

x=[1 2 3 4 5 6 7 8];

y=[-1.1 0.2 0.5 0.8 0.7 0.6 0.4 0.1];

p1=polyfit(x,y,1)

p2=polyfit(x,y,2)

p3=polyfit(x,y,3)

p4=polyfit(x,y,4)

p5=polyfit(x,y,5)

Подготовим данные для рисования кривых моделирующих полиномов с более мелким, чем в исходной таблице, шагом.

xx=0.5:0.1:8.5;

y1=polyval(p1,xx);

y2=polyval(p2,xx);

y3=polyval(p3,xx);

y4=polyval(p4,xx);

y5=polyval(p5,xx);

Нарисуем табличные точки кружками и моделирующие полиномы линиями разных цветов в одних осях (рис. 5.1).

plot(xx,y1,'r',xx,y2,'g',xx,y3,'b',xx,y4,'m',xx,y5,'k',x,y,'ko'), grid

Рис. 5.1. Аппроксимация полиномом

Для оценки погрешности аппроксимации вычислим погрешность моделирования в табличных точках

e1=sqrt(sum((y-polyval(p1,X)).^2))/length(y)

e2=sqrt(sum((y-polyval(p2,X)).^2))/length(y)

e3=sqrt(sum((y-polyval(p3,X)).^2))/length(y)

e4=sqrt(sum((y-polyval(p4,X)).^2))/length(y)

e5=sqrt(sum((y-polyval(p5,X)).^2))/length(y)

Результаты сведем в табл. 6.1. Из данных, приведенных в таблице, видно, что с увеличением степени полинома качество моделирования улучшается (погрешность уменьшается). Но не следует делать вывод, что всегда, чем выше порядок полинома, тем лучше, и для качественного приближения сразу же нужно брать максимально возможный порядок. При увеличении степени возможно ухудшение приближения – полином проходит почти через все табличные точки или очень близко от них, но плохо ведет себя в промежуточных точках, появляются осцилляции.

Таблица 6.1

Вектор коэффициентов p'	Порядок полинома	Аппроксимирующий полином	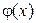Погрешность аппрокси-мации
[0.1143 -0.2393]		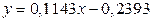	0,1771
[-0.1024 1.0357 -1.7750]		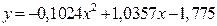	0,0619
[0.0177 -0.3410 1.9461 -2.6500]		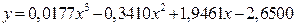	0,0306
[-0.0044 0.0961 -0.8146 3.0326 -3.3893]		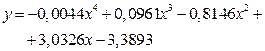	0,0200
[0.0013 -0.0332 0.3354 -1.7088 4.4880 -4.1750]		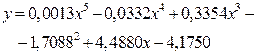	0,0169

На практике степень полинома можно оценить по следующему правилу: при увеличении порядка многочлена на единицу, погрешность аппроксимации должна уменьшаться на порядок. В нашем примере можно остановиться на полиноме третьей степени (погрешность уменьшилась с 0,06 до 0,03). Коэффициенты при старших степенях полиномов степени 4 и 5 по модулю значительно меньше, чем остальные коэффициенты. Этот факт так же служит подтверждением того, что порядок аппроксимирующего полинома становится избыточным, и следует прекратить его наращивание.

2.2. Аппроксимация произвольной функцией

по методу наименьших квадратов

Основное ограничение на вид моделирующей функции – она должна быть линейной относительно искомых коэффициентов. Аппроксимацию произвольной функцией по методу наименьших квадратов можно выполнить, используя Matlab-функцию lsqcurvefit, обращение к которой имеет следующий вид:

coeff = lsqcurvefit(f,x0,x,y);

где x, y – векторы значений аппроксимируемой функции; x0 – начальное значение параметров (коэффициентов) моделирующей функции; f – аппроксимирующая функция, вид которой задается пользователем; coeff – вектор уточненных параметров моделирующей функции.

Пример: Некоторая функция 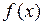задана таблицей значений. Известен или предполагается общий вид этой функции 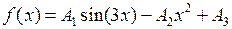, но неизвестны значения параметров (коэффициентов 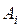, 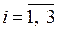). Требуется подобрать коэффициенты так, чтобы обеспечить минимум отклонений моделирующей кривой от узлов таблицы.

Решение: Для конкретности возьмем функцию 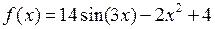. Поскольку точные значения коэффициентов известны, то будем иметь возможность сравнить решение. Вычислим табличные точки

x=0:0.5:7;

y=14*sin(3*x)-2*x.^2+4;

Сделаем вид, что значения коэффициентов не известны, зададим их стартовые значения, равными 1

x0=[1 1 1];

Опишем inline-функцию с неизвестными параметрами, размещенными в векторе a

f=inline('a(1)*sin(3*x)+a(2)*x.^2+a(3)','a','x');

Уточним значения коэффициентов при помощи функции lsqcurvefit, результат разместим в векторе coeff

coeff=lsqcurvefit(f,x0,x,y)

Вычислим значения модельной функции в узлах таблицы

ymodel=model(x,coeff);

hold on

Построим реальную функцию

fplot(@model,[0 7],'b-',[],[],coeff)

Прорисуем отсчеты моделирующей и реальной функций

plot(x,y,model,'bo',x,y,'r*')

hold off

grid

title('Моделирование произвольной функцией')

legend('Исходная функция','Отсчеты','Модель')

Здесь model –m-функция аргумента х с параметром, заданным вектором coeff

function y=model(x,coeff)

y=coeff(1)*sin(3*x)+coeff(2)*x.^2+coeff(3);

Результат построений приведен на рис. 5.2.

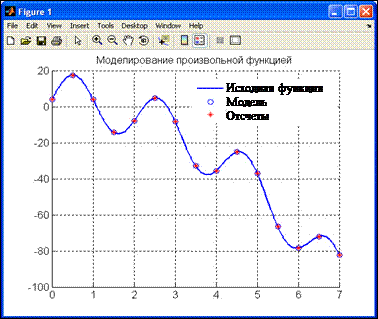
Рис. 5.2. Моделирование с помощью lsqcurvefit

Обратите внимание на очень важный момент: функция lsqcurvefit для своей работы требует первой в списке параметров указать функцию, первым формальным параметром которой являются искомые коэффициенты. А функция fplot, используемая нами для прорисовки плавной кривой, первым параметром предписывает указать функцию, в списке формальных параметров которой первым указывается аргумент х, и только потом – коэффициенты. Поэтому нельзя одну и туже функцию использовать в обоих случаях. При этом не имеет принципиального значения, какая именно функция используется: m или inline. Для обращения к lsqcurvefit мы могли бы написать следующую m-функцию:

function y=model2(coeff,x)

y=coeff(1)*sin(3*x)+coeff(2)*x.^2+coeff(3);

которая отличается от функции model только порядком следования формальных параметров. Напомню, что имена формальных параметров и в функции model, и в model2 могут быть любыми допустимыми в Matlab (совсем не обязательно называть их у, х и coeff). Впрочем, это касается не только m-функций, но и inline-объектов.

Отсчеты, заданные таблицей и полученные в результате моделирования (рис. 5.2), совпадают, т.к. исходные данные (и вид функции, и координаты функции) были заданы без погрешности. Коэффициенты, вычисленные lsqcurvefit, равны заданным значениям

coeff =

14.0000 -2.0000 4.0000

Дата добавления: 2014-11-08