Интерполяция

На практике интерполяцию выполняют, как правило, тогда когда имеется выборка отсчетов функции 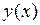, аналитическое выражение которой не известно, и требуется получить значения функции для х, лежащих между узлами таблицы. Интерполяция обычно выполняется кусочно – сколько интервалов между узлами таблицы, столько и интерполяционных функций. Интерполяционная кривая справедлива только для того участка таблицы, для которого она построена.

3.1. Кусочная интерполяция

Одномерная табличная интерполяция может быть выполнена функцией interp1, позволяющей решать задачу несколькими методами. Обращение к ней имеет следующий вид:

yi=interp1(x,y,xi, метод);

где х и у – векторы значений узлов таблицы и соответствующие им значения моделируемой функции; xi – вектор узлов интерполяции; метод – строковая константа, задающая метод интерполяции: 'nearest' – ступенчатая, 'linear' – линейная (принята по умолчанию), 'cubic' – кубическая, 'spline' – кубическими сплайнами. Функция не позволяет получить аналитические выражения интерполяционных функций (интерполянт), выдает только их значения между узлами таблицы.

Пример. Зададим синусоиду шестью точками и проведем кубическую интерполяцию на более мелкой сетке (рис. 5.3).

x=1:6;

y=sin(x);

xi=1:0.5:6;

xh=1:0.1:6;% абсциссы для рисования плавных кривых

model_cubic=interp1(x,y,xh,'cubic');

yh=sin(xh);% плавная кривая синусоиды

yc=interp1(x,y,xi,'cubic');

plot(xh,model_cubic,'k-.',xh,yh,'m-',xi,yc,'r*',x,y,'ko'), grid

legend('модель','sin(x)')

Рис. 5.3. Кусочная кубическая интерполяция синусоиды

Полученная модель лишь отдаленно напоминает синусоиду. Качество моделирования можно улучшить, задав большее количество узлов.

3.2. Кубические сплайны

Кубические сплайны – это сопряженные (плавно стыкующиеся друг с другом) многочлены третьей степени. Интерполяцию кубическими сплайнами осуществляет функция spline. Обращение

уi= spline(x,y,xi);

интерполирует значение вектора y, заданного при значениях аргумента, представленных в векторе х, и выдает значения моделирующей функции в виде вектора уi при значениях аргумента, заданных вектором хi. Если вектор х не указан, по умолчанию принимается, что он имеет такую же длину, как и вектор у, и любой его элемент равен порядковому номеру этого элемента. Шаг по х и по хi не обязательно должен быть постоянным (в частном случае хi может быть и скаляром). Моделируемая функция f (x) может быть задана и аналитически. Функция spline не позволяет получить аналитические выражения интерполяционных сплайнов (их коэффициенты). Но обращение

pp=spline(x,y);

возвращает так называемую вспомогательную рр-форму сплайнов. Коэффициенты же кубических сплайнов можно узнать, обратившись к функции unmkpp

[br,coefs]=unmkpp(pp);

В результате в векторе coefs будут размещены коэффициенты сплайнов, в br – разбиения по х. Значения кусочно-гладких сплайнов для заданных значений аргумента вычисляет функция ppval

ppval(pp,xi).

Пример. Зададим синусоиду шестью точками и проведем интерполяцию кубическими сплайнами на более мелкой сетке.

x=1:6;

y=sin(x);

xi=1:0.5:6;

yi=spline(x,y,xi)

xh=1:0.1:6;% абсциссы для рисования плавных кривых

yh=sin(xh);% кривая синусоиды

pp=spline(x,y);

[br,coefs]=unmkpp(pp);

modelsin=ppval(pp,xh);

plot(x,y,'ko',xi,yi,'r*',xh,yh,'m-',xh,modelsin,'k-'), grid

В результате работы программы будут получены одиннадцать отсчетов интерполяционных сплайнов: шесть из них будут совпадать с табличными значениями, пять – получены для промежуточных точек х = {1,5 2,5 3,5 4,5 5,5}

ys =

0.8415 1.0194 0.9093 0.5902 0.1411 -0.3497 -0.7568 -0.9676 -0.9589 -0.7298 -0.2794

В частности для xi = 1,5 получено значение уi = 1,0194. Решение (рис.5.4) демонстрирует погрешность интерполяции: значение 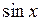не может быть больше единицы. Матрица coefs размером 5×4 будет содержать пять наборов (по числу интервалов между узлами таблицы), в каждом – по четыре коэффициента кубических сплайнов.

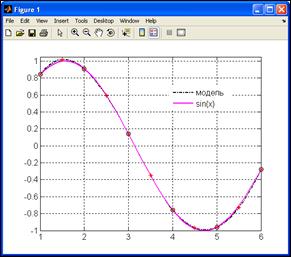
Рис. 5.4. Интерполяция кубическими сплайнами

3.3. Интерполяция произвольной нелинейной функцией

Интерполяция произвольной нелинейной функцией может быть выполнена с помощью fsolve, решающей систему нелинейных уравнений. Обращение к ней имеет вид:

coef=fsolve(mfile,x0);

где coef – искомые параметры интерполирующей функции; х0 – начальное приближение к coef; mfile – указатель на имя m-файла, описывающего систему уравнений.

Пример: пусть неизвестная функция задана таблицей значений

х
у	6,5		53,5

Необходимо получить аналитическое выражение для этой функции. Выберем вид интерполяционной функции, воспользовавшись графоаналитическим методом – построим исходные точки. График функции в виде точек таблицы похож на степенную функцию (рис. 5.6). Выберем в качестве интерполяционной функцию вида 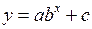. Так как функция содержит три неизвестных коэффициента (a, b и с, причем b входит нелинейно), то для их определения составим систему из трех уравнений, выбрав в качестве аргументов три узла таблицы х = 1, 3 и 5. Получим

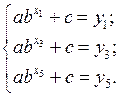
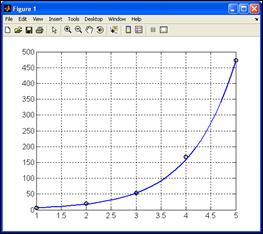
Рис. 5.6. Интерполяция степенной функцией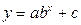

Подставим в систему соответствующие значения х и у из таблицы. Запишем m-функцию

function system=sysur(coef)

global y x

system=[coef(1)*coef(2)^x(1)+coef(3)-y(1);

coef(1)*coef(2)^x(3)+coef(3)-y(3);

coef(1)*coef(2)^x(5)+coef(3)-y(5)];

и файл-сценарий

global y x;

x=1:5;

y=[6.5 20 53.5 167 473];

x0=[1; 1; 1;];

coef=fsolve(@sysur,x0)

В результате выполнения скрипта с m-функцией получим следующий вектор коэффициентов моделирующей функции

coef =

1.9850

2.9876

0.5698

Следовательно, интерполяционная функция будет иметь вид у _м=1,9850·2,9876 ^х +0,5698. Моделирующая кривая у _м(х) в обязательном порядке пройдет через первую, третью и пятую точки таблицы, по которым были определены ее параметры, но необязательно через вторую и четвертую (рис. 5.6).

Примечание: по правилам использования стандартной функции fsolve m-функция, описывающая решаемую систему уравнений, должна иметь один формальный параметр – искомые коэффициенты. Для пересылки в файл-функцию sysur значений векторов х и у в головной программе и в функции объявляются глобальные данные (после слова global указывается перечень глобальных переменных через пробел).

Дата добавления: 2014-11-08