Общие сведения. Вычисление функций разложением в ряд

Вычисление функций разложением в ряд

Итерационными (пошаговыми) алгоритмами называются алгоритмы, в которых на каждом шаге используется одна и та же формула, выраженная через значения, полученные на предыдущих шагах алгоритма. Выполнение такого алгоритма сводится к генерации некоторой числовой последовательности результатов 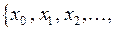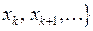, где k –номер итерации, – значение, полученное на k -м шаге процесса.

Итерационной формулой в общем виде называется выражение

,

позволяющее генерировать последующие члены последовательности через вычисленные ранее (на предыдущих шагах алгоритма). Чаще же всего итерационные формулы имеют более простой вид

.

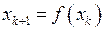В любом случае итерационная последовательность должна иметь своим пределом искомое значение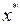

.

Если такой предел существует, то итерационный процесс называется сходящимся, иначе – расходящимся.

Реальный вычислительный процесс всегда должен заканчиваться при конечном значении k, поэтому всегда возникает проблема выбора условия окончания итераций – так называемого критерия сходимости. Наиболее часто на практике используются следующие критерии сходимости:

1. Абсолютное изменение параметра на соседних шагах итерационного процесса

.

2. Относительное изменение параметра на соседних шагах

.

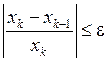Здесь 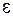– некоторое наперед заданное малое значение, определяющее точность (погрешность) нахождения решения.

При решении конкретных задач возможно применение специфических критериев или комбинации нескольких критериев.

Обобщенная блок-схема итерационных алгоритмов изображена на рис. 7.1.

Рис. 7.1. Обобщенная блок-схема итерационного алгоритма

Дата добавления: 2014-11-08