Решение систем нелинейных уравнений

Решение систем нелинейных уравнений в Matlab осуществляется функцией fsolve, обращение к которой имеет вид:

х=fsolve(func,x0);

где х – вектор решения; х0 – вектор начального приближения к х; func – ссылка на имя m-функции, описывающей систему уравнений.

Пример: пусть необходимо решить следующую систему нелинейных уравнений:

Данная система имеет бесконечное количество корней. Найдем положительные корни, не превосходящие 3.

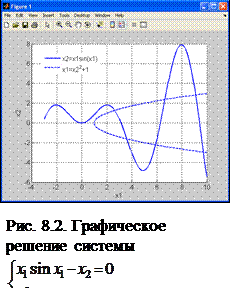Выполним отделение корней, ведь для обращения к fsolve нам придется задать начальное приближение. Построим графики функций и определим точки их пересечения.

x1=-3:0.1:10;

x2=sin(x1).*x1;

hold on

plot(x1,x2)

x2=-3:0.1:3;

x1=x2.^2+1;

plot(x1,x2,'--')

grid

hold off

legend('x2=x1sin(x1)','x1=x2^2+1')

xlabel('x1')

ylabel('x2')

Из графиков (рис. 8.2) следует, что при рассматриваемых ограничениях на значение корней система имеет только одну пару корней, приближенные значения которых х ₁ =2,5 и х ₂ =1,2.

Составим m-функцию, описывающую систему уравнений

function fun=nonlinearsystem(x)

fun=[x(1).*sin(x(1))-x(2);

x(2).^2-x(1)+1];

и файл-сценарий с обращением к fsolve для уточнения решения

x0=[2.5; 1.2;];

[xx, fx]=fsolve(@nonlinearsystem,x0,optimset('TolFun',1e-9))

В результате получим следующее решение (пару корней и значения левых частей обоих уравнений при этих корнях):

xx =

2.6349

1.2786

fx =

1.0e-015 *

0.2220

0.4441

Примечание. В примере при обращении к fsolve в качестве третьего входного аргумента указана одна из возможных настроек опций, управляющих решением: задана относительная погрешность TolFun значения функции в точке корня.

Дата добавления: 2014-11-08