Решение одного нелинейного уравнения

Найти действительный нуль функции одной переменной позволяет функция fzero, которая в зависимости от формы задания функции реализует следующие хорошо известные численные методы: деления отрезка пополам, секущей и обратной квадратичной интерполяции. Обращение к функции

z = fzero(func, x0);

где х0 – начальное значение аргумента, в окрестности которого отыскивается действительный корень функции func; z – найденное значение корня. Начальное значение х0 можно задать в виде вектора – границ интервала поиска корня. На концах указанного интервала функция должна иметь значения разных знаков. В противном случае будет выдано сообщение об ошибке.

Входных аргументов у функции fzero может быть и больше. Например, можно указать третий фактический параметр

z = fzero(func, x0, options);

здесь options – управляющая структура задания дополнительных параметров для управления вычислительным процессом и контроля за ним. Формирование структуры выполняется функцией optimset. В общем случае аргументы задаются попарно по схеме

options=optimset('вид контроля',значение);

Наиболее часто используемые параметры optimset приведены в табл. 8.1.

Таблица 8.1

Вид контроля	Значение	Результат
Display	'off'	Информация о вычислительном процессе не выводится
'iter'	Выводится информация о каждом шаге вычислительного процесса
'final'	Выводится информация только о завершении вычислительного процесса
'notify'	Выводится предупреждение, если процесс не сходится (используется по умолчанию)
MaxIter	положительное целое число	Максимальное количество итераций вычислительного процесса
TolFun	положительное вещественное число	Точность по функции для останова вычислений
TolX	положительное вещественное число	Точность по аргументу для останова вычислений

Вызов функции optimset без входных аргументов позволяет получить в командном окне Matlab перечень всего множества параметров с их допустимыми значениями (в фигурных скобках указываются значения, принятые по умолчанию).

Список выходных аргументов функции fzero также может быть расширен

[z, fval,flag] = fzero(func, x0, tol, trace);

где fval – реальное значение функции в найденном приближении к корню z, flag – признак решения: 1 – корень найден; -1 – не удалось определить интервал со сменой знака функции; -3 – в процессе вычислений получена бесконечность (inf) или выполнена операция с неопределенным результатом (nan), например, деление нуля на ноль; -4 – в ходе вычислений получилось комплексное значение; -5 – решение сошлось в особую точку.

Пример: Найдем корни уравнения .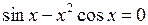

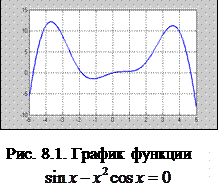Выполним отделение корней графическим методом. Построим график функции на интервале [-5; 5]:

fplot('sin(x)-x.^2.*cos(x)', [-5 5])

grid

Из графика функции (рис. 8.1) видно, что у нее 4 корня: вблизи х =-5, х =-2, х=0 и х =5. Уточним корень вблизи х =-5:

fx=inline('sin(x)-x.^2.*cos(x)');

[x1, fval]=fzero(fx,-5)

Получим уточненное значение корня x1 = -4.7566 и значение функции в нем fval = 2.6645e-15.

За одно обращение к fzero можно уточнить только один корень. Важной особенностью fzero является и то, что она вычисляет только вещественные корни и только те из них, в которых функция меняет знак, а не касается оси абсцисс. Так, например найти корень уравнения х ² = 0 при помощи fzero не удастся! Нет интервалов, на которых функция меняет свой знак. А корень есть!

Дата добавления: 2014-11-08